Матричная запись системы линейных уравнений

AX = B,

где

Матрицу A называют матрицей (или основной матрицей) системы. Матрицу

называют расширенной матрицей системы, а матрицу 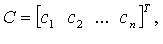для которой AС = В, - вектор-решением системы.

Система уравнений - это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Решением системы уравненийназывается упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.

Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.

При решении систем уравнений методом обратной матрицы используются вычисления определителя матрицы (Для вычисления матрицы, обратной к основной матрице системы уравнений). Для того, чтобы матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля, тоесть матрица должна быть невырожденной.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

9. Равносильность систем линейных уравнений. Расширенная матрица системы. Элементарные преобразования.

Матрица системы, к которой присоединен столбец свободных

членов, называется расширенной матрицей системы:

Перестановка уравнений системы, прибавление к одному уравнению системы другого уравнения, умножение уравнения на число, отличное от нуля — такие преобразования системы называются элементарными преобразованиями системы

Расширенная матрица— матрица системы, дополненная столбцом свободных членов

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

§ перестановка местами любых двух строк матрицы;

§ умножение любой строки матрицы на константу , ;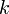

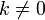§ прибавление к любой строке матрицы другой строки, умноженной на константу , .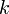

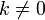В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу 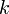, 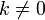и прибавление к любой строке матрицы другой строки, умноженной на константу , .

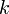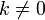Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение 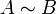указывает на то, что матрица 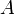может быть получена из 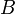путём элементарных преобразований (или наоборот