Линейная зависимость и независимость векторов. Базис.

Говорят, что вектор 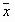пространства Rⁿ линейно выражается через векторы 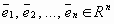, если его можно представить в виде линейной комбинации этих элементов 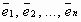, т.е. представить в виде .

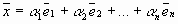Определение. Если хотя бы один вектор системы векторов 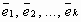из Rⁿ линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.

Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.

Свойства базиса, естественный базис, координаты вектора в заданном базисе

Итак установлено, что в пространстве Rⁿ существует система из n линейно независимых векторов, а любые n+1 вектора линейно зависимы.

Число n — размерность пространства Rⁿ.

Определение. Любая упорядоченная линейно независимая система n векторов 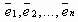пространства арифметических векторов Rⁿ называется базисом в Rⁿ .

Нетрудно показать, что любой вектор 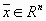единственным образом выражается через векторы базиса: 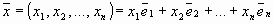. (На лекции единственность доказана).

Числа 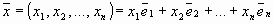называют координатами вектора 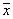в базисе .

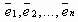Линейно независимая система векторов

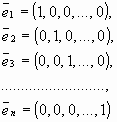
образует базис в Rⁿ , который называют естественным базисом в Rⁿ.

Скалярное произведение. Длина вектора. Геометрическая интерпретация в случае двух и трех измерений.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов 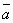, 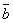обозначается символом 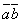(порядок записи сомножителей безразличен, то есть ).

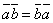Если угол между векторами 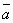, 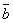обозначить через 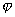, то их скалярное произведение можно выразить формулой

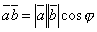
Скалярное произведение двух ненулевых векторов a и bназывается число, равное произведению длин этих векторов на косинус угла между ними.

( страница 38-39)

Длиной или модулем вектора называется длина соответствующего направленного отрезка.

Модуль вектора a обозначается 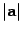. Вектор a называется единичным, если .

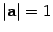Длина вектора

Понятие вектора

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Направление вектора (от начала к концу) на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначается символом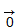

Длиной ненулевого вектора 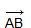называется длина отрезка AB. Длина вектора 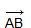(вектора 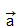) обозначается так: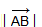 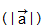. Длина нулевого вектора считается равной нулю: .
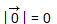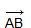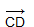Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой ил на параллельных прямых. Если два ненулевых вектора и коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы 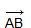и 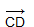называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы 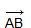и 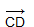называютсяпротивоположно направленными. Нулевой вектор принято считать сонаправленным с любим вектором.