Введение вспомогательного аргумента
Уравнения вида 
. Для его решение, разделим левую часть уравнения на квадратный корень из суммы его коэффициентов, т. е. на 
, чтобы уравнение не изменилось, на это же выражение умножим левую часть уравнения, т. е. выполним следующие преобразования:
, где
.
Пример 183. Решить уравнение 
.
Решение
Разделим и умножим левую часть уравнения на 
, получим уравнение:
,
,
Ответ: 
.
Пример 184. Решить уравнение 
.
Решение
Преобразуем уравнение: разделим и умножим левую часть уравнения на корень квадратный из суммы квадратов коэффициентов при sinx и cosx, т. е. на
.
Уравнение примет вид: 
Ответ: 
.
Замечание. Мы не совсем строго решили второе уравнение, определяющее значение вспомогательного аргумента 
. Из того, что 
получаем 
.
Дело в том, что этот аргумент нами выбирается произвольно, сами. Поэтому берем лишь одно частное решение, какое нам нравится. Обычно выбирается угол в первой четверти.
Пример 185. Решить уравнение 
.
Решение
Перенесем число 2 в правую часть и разделим обе части уравнения на корень квадратный из суммы квадратов коэффициентов при sinx и cosx, получим:
.
Заменим 
. Получим уравнение
.
Ответ: 
.
Пример 186. Решите уравнение 
Решение
Преобразуем уравнение
Пусть 
, получим квадратное уравнение 
,
.
, значит,
, следовательно, уравнение 
имеет решения.
.
Ответ: 
.
Пример 187. Решить уравнение 
.
Решение
Преобразуем уравнение: 
.
Разделим обе части уравнения на 2, так как 
, получим:
.
Заменим в левой части уравнения 
, а в правой части уравнения 
. Получим уравнение:
,
,
.
Ответ: 
Задание 9
Решите уравнение
188. 
. 189. 
.
190. 
. 191. 
.
192. 
. 194. 
.
195. 
. 196. 
.
197. 
. 198. 
.
199. 
.
Системы тригонометрических уравнений
200. Решите систему уравнений: 
Решение
Преобразуем систему 
Ответ: 
201. Решите систему уравнений: 
Решение
Из первого уравнения выразим x и подставим во второе уравнение системы:
Решим второе уравнение:
Отсюда находим:
.
Найдем значения x: 
.
Ответ: 
202. Решите систему уравнений: 
Решение
Выразим из первого уравнения y и подставим во второе уравнение:
Решим второе уравнение системы: 
.
Получим совокупность уравнений:
Найдем значения y:
.
Ответ: 
Задание 10
Решите системы уравнений:
203. 
204. 
205. 
206. Решить систему уравнений 
Решение
Сложим почленно уравнения системы и вычтем из первого уравнения второе, получим систему уравнений:
Ответ: 
Замечание. В каждом уравнении системы необходимо для множеств целых чисел использовать различные буквы!
Если бы мы использовали для множества решений двух уравнений одну букву
то после сложения-вычитания двух уравнений, получили бы решение в виде
Произошла бы "потеря решений", что недопустимо!
207. Решить систему уравнений: 
Решение
Сложим левые и правые части уравнений системы, получим:
.
Применим к левой части уравнения формулу косинуса разности двух углов:
.
Получим уравнение: 
.
Вычтем из второго уравнения первое: 
.
Применим к левой части уравнения формулу косинуса суммы двух углов:
.
Получим уравнение: 
.
Из полученных двух уравнений составим систему:
;
вычитая из второго уравнения первое, найдем значения y:
.
Ответ: 
208. Решить систему уравнений: 
Решение
Сложим второе уравнение с первым, а затем вычтем из второго уравнения первое. В первом случае, применим формулу косинуса разности двух углов, а во втором косинуса суммы двух углов:
.
.
Получим новую систему уравнений:
,
.
Ответ: 
.
Задание 11
Решить систему уравнений:
209. 
210. 
211. 
Ответы
к заданиям «Основные методы решения тригонометрических уравнений»
К заданию 1
29. 
. 33. 
34. 
. 35. 
36. 
37. 
К заданию 2
60. 
. 63. 
.
67. 
. 68. 
.
69. 
. 70. 
.
71. 
. 73. 
.
74. 
.
К заданию 3
97. 
99. 
.
К заданию 5
123. 
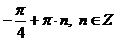. 124. 
.
126. 
.
К заданию 6
139. 
141. 
142. .
К заданию 7
157. 
. 158. 
.
161. 
К заданию 9
195. 
196. 