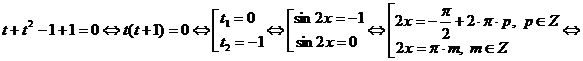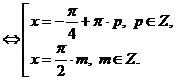Применение формул приведения
Пример 82. Решите уравнение 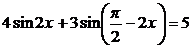 .
.
Решение
Преобразуем уравнение: 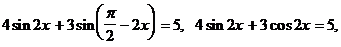
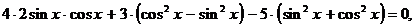
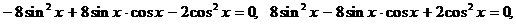
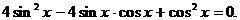
Полученное уравнение - однородное, 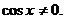
Разделим обе части уравнения на 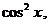 приходим к уравнению:
приходим к уравнению:
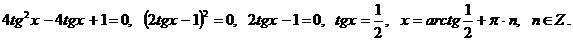
Ответ: 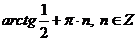 .
.
Пример 83. Решите уравнение
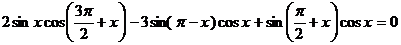 .
.
Решение
I-й способ
Преобразуем уравнение, используя формулы приведения, получим:
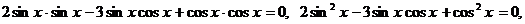
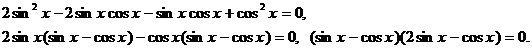
Получим совокупность уравнений:
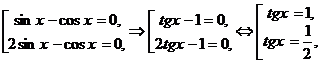
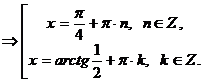
Ответ: 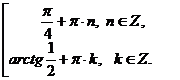
II-й способ
Применим формулы приведения:
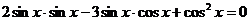 - это однородное уравнение второй степени,
- это однородное уравнение второй степени, 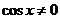 .
.
Разделим обе части уравнения на 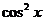 ,
, 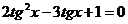 .
.
Пусть tgx = t, тогда получим: 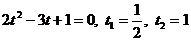 .
.
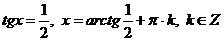 ,
, 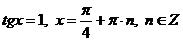 .
.
Ответ: 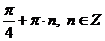 ;
; 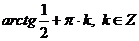 .
.
Пример 84. Решить уравнение 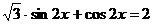 .
.
Решение
Преобразуем уравнение к однородному:
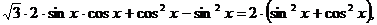
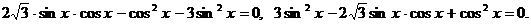
Полученное уравнение - однородное. Разделим обе части этого уравнения на 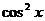 (
( 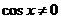 , ибо, в противном случае, из уравнения следует, что и
, ибо, в противном случае, из уравнения следует, что и 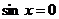 , что невозможно, так как тогда не будет выполняться основное тригонометрическое тождество
, что невозможно, так как тогда не будет выполняться основное тригонометрическое тождество 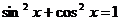 ). В результате деления на
). В результате деления на 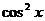 , получим:
, получим: 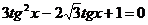 .
.
Положим 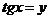 , получим
, получим 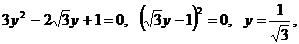
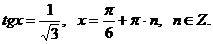
Ответ: 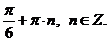
Пример 85. Решить уравнение 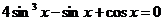 .
.
Решение
Это уравнение не является однородным. Перепишем его иначе:
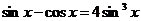 . Умножим левую часть уравнения на 1, а точнее на её значение
. Умножим левую часть уравнения на 1, а точнее на её значение 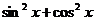 . После приведения подобных слагаемых имеем:
. После приведения подобных слагаемых имеем:
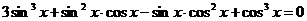 . Это однородное уравнение третьей степени относительно sinx и cosx,
. Это однородное уравнение третьей степени относительно sinx и cosx, 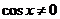 . Если cosx = 0, то из уравнения следует sinx=0, что невозможно.
. Если cosx = 0, то из уравнения следует sinx=0, что невозможно.
Разделим обе части уравнения на 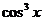 , получим:
, получим: 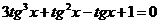 .
.
Положим tgx = y, получим 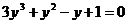 . Нетрудно заметить, что y = -1 является корнем уравнения. Разделим левую часть на y + 1, получим:
. Нетрудно заметить, что y = -1 является корнем уравнения. Разделим левую часть на y + 1, получим:
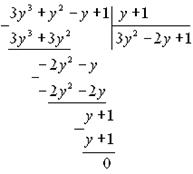
Уравнение примет вид: 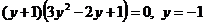 .
.
Уравнение 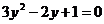 не имеет корней, так как дискриминант трехчлена отрицателен.
не имеет корней, так как дискриминант трехчлена отрицателен. 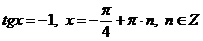 .
.
Ответ: 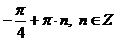
Пример 86. Решить уравнение 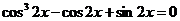 .
.
Решение
I-й способ
Преобразуем уравнение:
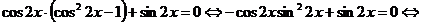
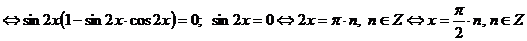 ;
;
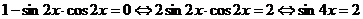 - решений не имеет.
- решений не имеет.
Ответ: 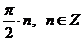 .
.
II-й способ
Преобразуем уравнение: 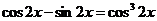 . Умножим левую часть уравнения на
. Умножим левую часть уравнения на 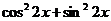 , получим:
, получим: 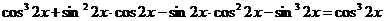 .
.
После приведения подобных слагаемых получим однородное уравнение третьей степени относительно sinx и cosx: 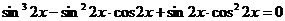 ,
, 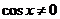 .
.
Разделим обе части уравнения на 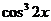 , получим:
, получим: 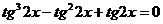 .
.
Пусть tgx = y, тогда 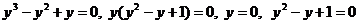 - не имеет корней.
- не имеет корней.
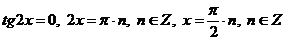 .
.
Ответ:  .
.
Пример 87. Решить уравнение 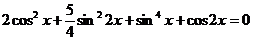 .
.
Решение
Преобразуем уравнение: 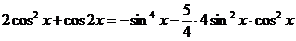 ,
,
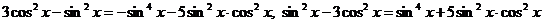 ,
,
Умножим левую часть уравнения на 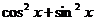 , получим:
, получим:
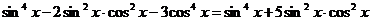 ,
,
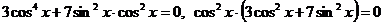 ,
,
Последнее уравнение - однородное четвертой степени относительно sinx и cosx.
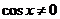 . Если допустить, что cosx = 0, тогда из уравнения следует sinx = 0, что невозможно. Разделим обе части уравнения на
. Если допустить, что cosx = 0, тогда из уравнения следует sinx = 0, что невозможно. Разделим обе части уравнения на 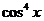 ,
, 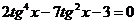 .
.
Пусть 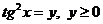 , получим квадратное уравнение:
, получим квадратное уравнение: 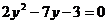 ,
,
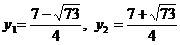 .
. 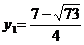 - не удовлетворяет условию
- не удовлетворяет условию 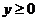 и является посторонним корнем.
и является посторонним корнем.
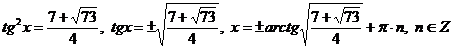
Ответ: 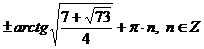 .
.
Задание 3
88. 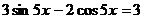 . 89.
. 89. 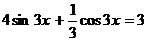 .
.
90. 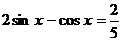 . 91.
. 91. 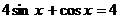 .
.
92. 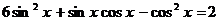 . 93.
. 93. 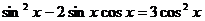 .
.
94. 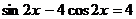 . 95.
. 95. 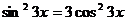 .
.
96. 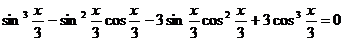 .
.
97. 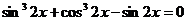 . 98.
. 98. 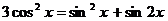 .
.
99. 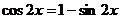 . 100.
. 100. 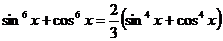 .
.
101. 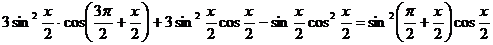 .
.
102. 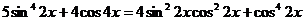 .
.
103. 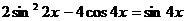 . 104.
. 104. 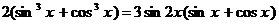 .
.
4. Для преобразования уравнений было использовано основное тригонометрическое тождество 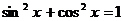 . Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.
. Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.
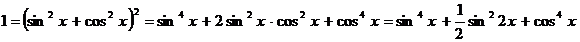 ,
,
отсюда находим 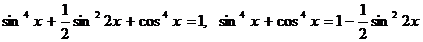 .
.

Далее,
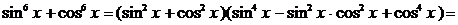
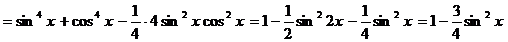 .
.

Преобразуем сумму 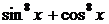 , используя формулу (4).
, используя формулу (4).
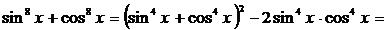
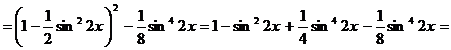
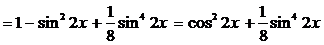 .
.
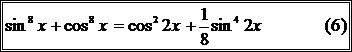
Выше приведенные формулы очень часто используются при решении тригонометрических уравнений, и не только однородных.
Пример 105. Решите уравнение
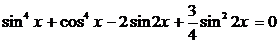 .
.
Решение
Преобразуем уравнение, используя формулу (4): 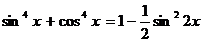 , получим уравнение:
, получим уравнение: 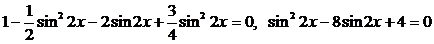 .
.
Пусть 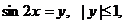 приходим к квадратному уравнению:
приходим к квадратному уравнению:
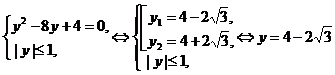 ,
,
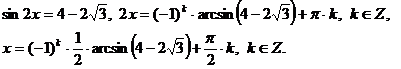
Ответ: 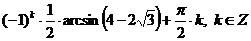 .
.
Пример 106. Решите уравнение
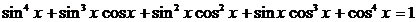 .
.
Решение
Преобразуем уравнение, используя формулу (4): 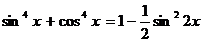 , получим уравнение:
, получим уравнение: 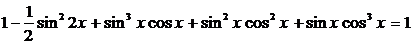 ,
,
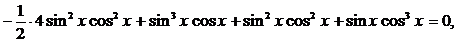

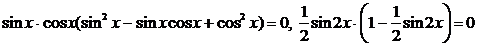 ,
,
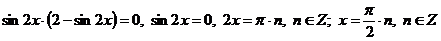 .
.
Уравнение 2 - sin2x = 0, sin2x = 2 не имеет решений.
Ответ:  .
.
Пример 107. Решите уравнение 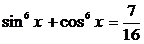 .
.
Решение
Преобразуем уравнение, используя формулу: 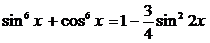 , получим:
, получим: 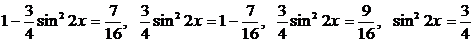
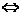
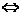
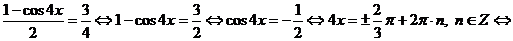
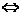
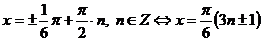 .
.
Ответ: 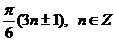 .
.
Пример 108. Решите уравнение 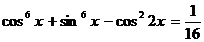 .
.
Решение
Преобразуем уравнение, используя формулу: 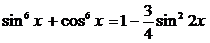 , получим:
, получим:
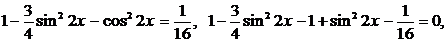
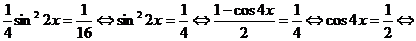 .
.
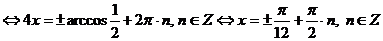
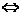
 .
.
Ответ: 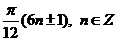 .
.
Пример 109. Решите уравнение
 .
.
Решение
Преобразуем уравнение, используя формулы:
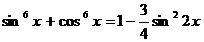 и
и 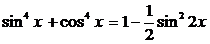 , получим:
, получим:
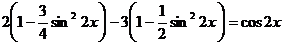 ,
,
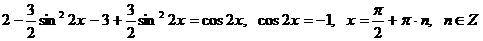 .
.
Ответ: 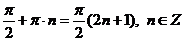 .
.
Пример 110. Решите уравнение 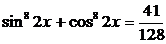 .
.
Решение
Преобразуем уравнение, используя формулу (6)
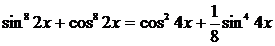 , получим уравнение:
, получим уравнение:
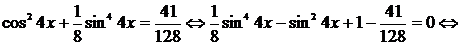
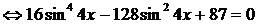 . Пусть
. Пусть 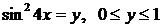 , получим:
, получим:
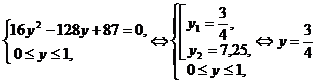
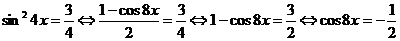
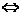
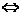
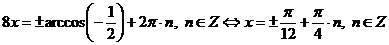 .
.
Ответ: 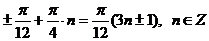 .
.
Задание 4
111. 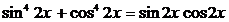 . 112.
. 112. 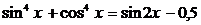 .
.
113. 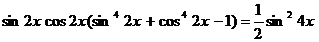 .
.
Метод замены переменных
4.1. Замена 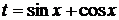 .
.
Пусть дано некоторое тригонометрическое уравнение F(x) = 0. Обозначим через g(x) функцию 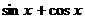 и введем новое неизвестное
и введем новое неизвестное 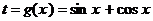 . Если удастся выразить функцию F(x) через t, т. е. представить ее в виде
. Если удастся выразить функцию F(x) через t, т. е. представить ее в виде 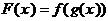 , то решение уравнения F(x) = 0 будет сведено к решению уравнения f(t) = 0. Разумеется, не всегда левую часть F(x) удается достаточно просто выразить через
, то решение уравнения F(x) = 0 будет сведено к решению уравнения f(t) = 0. Разумеется, не всегда левую часть F(x) удается достаточно просто выразить через 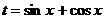 .
.
Мы рассмотрим несколько случаев, когда это удается сделать.
Введем (в некотором тригонометрическом уравнении) новое неизвестное 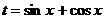 , тогда, применяя тождество
, тогда, применяя тождество
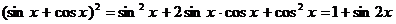 , находим
, находим
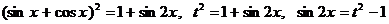 .
.
Ясно, что если уравнение содержит сумму функций 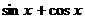 и синус двойного угла
и синус двойного угла 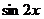 , тогда его можно выразить через t.
, тогда его можно выразить через t.
Если левая часть тригонометрического уравнения F(x) = 0 может быть выражена через 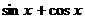 и
и 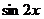 , то целесообразно применить замену неизвестного по формулам
, то целесообразно применить замену неизвестного по формулам 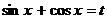 ,
, 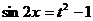 .
.
Пример 114. Решите уравнение 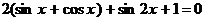 .
.
Решение
Пусть 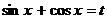 , тогда
, тогда 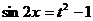 , получим квадратное уравнение:
, получим квадратное уравнение:
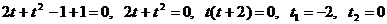 .
.
Получим совокупность уравнений:
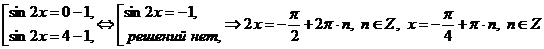 .
.
Ответ: 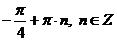 .
.
Замечание. Уравнение 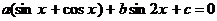 имеет решения в том и только в том случае, когда дискриминант уравнения
имеет решения в том и только в том случае, когда дискриминант уравнения 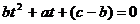 неотрицателен и по крайней мере один из корней этого уравнения удовлетворяет условию
неотрицателен и по крайней мере один из корней этого уравнения удовлетворяет условию 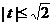 , так как
, так как 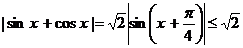 .
.
Аналогично решаются уравнения вида 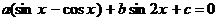 .
.
Здесь удобно положить 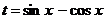 и тогда
и тогда 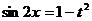 .
.
Пример 115. Решите уравнение 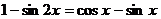 .
.
Решение
Й способ
Положим 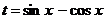 , тогда
, тогда 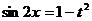 ,
, 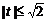 , получим уравнение:
, получим уравнение:
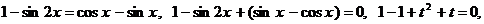
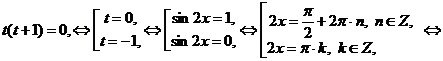
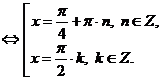
Ответ: 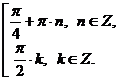
Й способ
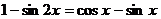 . Преобразуем уравнение, зная, что
. Преобразуем уравнение, зная, что 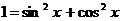 :
:
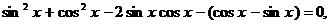
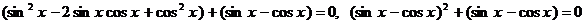 ,
,
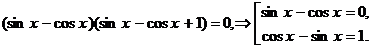
Дальнейшее решение такое же, как и в первом способе. Применяя второй способ, мы обходимся без введения новых переменных и без подстановки, но использовать его может лишь опытный человек, который имеет достаточно большой навык в решении тригонометрических уравнений, искусственных преобразованиях и т. п.
Пример 116. Решите уравнение 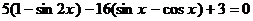 .
.
Решение
Положим 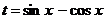 , тогда
, тогда 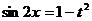 ,
, 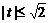 , получим уравнение:
, получим уравнение:
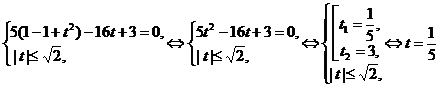
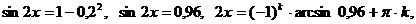 .
.
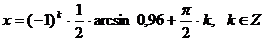 .
.
Ответ: 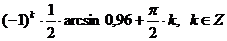 .
.
Пример 117. Решите уравнение 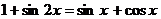 .
.
Решение
Пусть 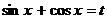 , тогда
, тогда 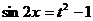 ,
, 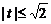 получим квадратное уравнение:
получим квадратное уравнение: 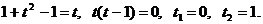
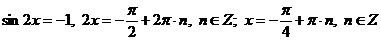 ;
;
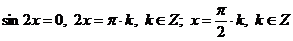 .
.
Ответ: 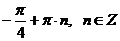 ;
; 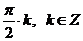 .
.
Пример 118. Решите уравнение 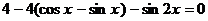 .
.
Решение
Положим 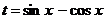 , тогда
, тогда 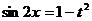 ,
, 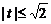 , получим уравнение:
, получим уравнение:
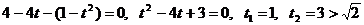 - не удовлетворяет условию
- не удовлетворяет условию 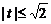 и является посторонним корнем.
и является посторонним корнем.
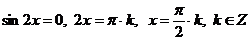 .
.
Ответ: 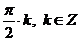 .
.
Пример 119. Решите уравнение 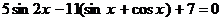 .
.
Решение
Пусть 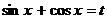 , тогда
, тогда 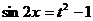 ,
, 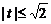 получим уравнение:
получим уравнение:
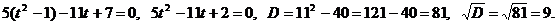
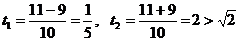 - не удовлетворяет условию
- не удовлетворяет условию 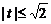 и является посторонним корнем.
и является посторонним корнем.
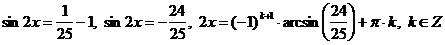 ,
,
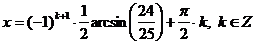 .
.
Ответ: 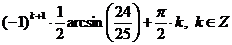 .
.
Пример 120. Решите уравнение 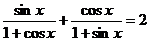 .
.
Решение
Область допустимых значений: 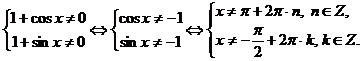
Преобразуем уравнение: 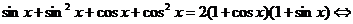
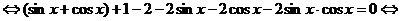
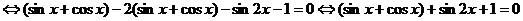 .
.
Применим подстановку 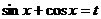 , тогда
, тогда 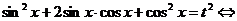
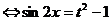 , получим уравнение
, получим уравнение