Достаточные условия интегрируемости

Теорема 2. Если выполнено одно из следующих условий :

• функция f(x) непрерывна на отрезке [a, b ];
• функция f(x) ограничена на отрезке [a, b] и имеет на этом отрезке конечное число точек разрыва;
• функция f(x) монотонна на отрезке [a, b],

то f(x) интегрируема на отрезке [a, b] и, следовательно,

b ∫ a f(x) dx

существует.

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

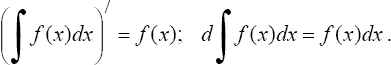
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

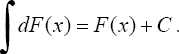
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

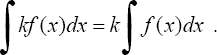
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Интеграл с переменным верхним пределом.

Если функция f(t) непрерывна в окрестности точки t = x, то в этой точке функция Ф(x) дифференцируема, и .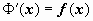
Другими словами, производная определённого интеграла от непрерывной функции по верхнему пределу равна значению подынтегральной функции в этом пределе.

По существу, любая непрерывная функция f(x) имеет первообразную, и эта первообразная определяется формулой 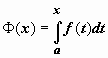. Другим важным следствием этой теоремы является формула Ньютона-Лейбница, или основная формула интегрального исчисления.

Формула Ньютона-Лейбница.

Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если 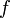непрерывна на отрезке 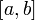и 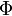— ее любая первообразная на этом отрезке, то имеет место равенство:

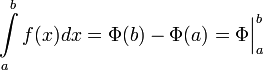
52)Формула замены переменной в определённом интеграле.

Определенный интеграл 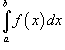по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):

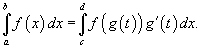
Новые пределы интегрирования по переменной t определяются выражениями

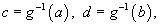
где g ^-1 - обратная функция к g, т.е. t = g ^-1(x).

Формула замены переменной в определённом интеграле.

В этом случае формула интегрирования по частям имеет вид:

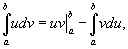
где 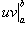означает разность значений произведения функций uv при x = b и x = a.

Формула трапеций и формула Симпсона.

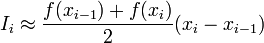
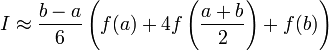
Несобственные интегралы с бесконечными пределами.

Несобственным интегралом (нс. и.) 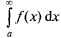от непрерывной на 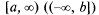функции 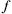(х) называется

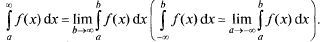
Несобственные интегралы от разрывных функций.

Пусть функция f(x) непрерывна при a ≤ x < b и имеет точку разрыва при x = b. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой

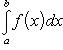
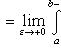
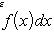
и называется сходящимся или расходящимся в зависимости от того, существует или не существует предел правой части равенства.