Формулы Виета. Кратные корни.

Формулы Виета дают связь между коэффициентами многочлена и его корнями (для приведенного уравнения, т.е. такого уравнения, у которого старший коэффициент равен единице).

Рассмотрим многочлен:

f(x)=xⁿ + a₁ x^n-1 +…+a_n .

Пусть a₁,…,a_n 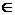P — коэффициенты многочлена, 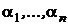— его корни. Можно записать (см. § 7, следствие 1):

f(x) = (x-α₁)(x-α₂)…(x-α_n).

Чтобы получить x^n-1 из каждой скобки надо взять x, за исключением одной скобки, из которой взят а_i, чтобы получить x^n-2 надо взять x из всех скобок, за исключением двух и т.д. Получим

a₁ = ( α₁+α ₂+…+ α_n )

a₂ = α₁α₂+…+ (1)

…

a_n = (-1)ⁿα₁ …α_n

Если мы домножим каждое равенство из (1) на (-1) в степени, равной индексу а_i, то мы получим привычные нам формулы Виетта.

-a₁ = α₁+α₂+…+α_n

a₂ = α₁α₂ +…+ (2)

……………..

(-1)ⁿ a_n = α₁… α_n

Кратные корни.

_{Пусть для f(x) = (x-α)}^k _{f 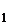(x) ; f 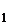(α)≠0, т.е. 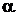— корень кратности .}

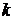_{Теорема 1. Если α — корень кратности k для многочлена, то α — корень кратности k-1 для его производной.}

◄ Доказательство следует из теоремы о кратности неприводимых множителей (т.2, § 5). ►

Упражнение.Верно ли утверждение,обратное этой теореме?

ТЕМА 4. ГРУППА.КОЛЬЦО. ПОЛЕ.

Бинарная агебраическая операция.

Пусть Х не пустое множество, X² — скалярный квадрат множества X, т.е. X²={(a,b)| a,bÎX}.

Определение 1. Отображение f:X²®X называется бинарной алгебраической операцией (БАО), то есть каждой паре элементов (a,b) множества X ставится в соответствие элемент сÎX.

Элемент c называется композицией элементов a и b, обычно записывают c=a°b ( где ° — обозначение кокой-то бинарной алгебраической операции ).

Примеры:

1) Вкачестве множества X возьмем N — натуральные числа, в качестве операции +:

(a,b)®a+b — отображение и

c=a+b — сумма.

2) Множество матриц над полем P с операциями +, *.

Если X — конечное множество, например X={x₁, x₂, ¼ ,x_n}, то алгебраическую операцию удобно задавать таблицей:

	x1 x2 x3 … xn
x1
x2 x3 … xn

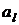В клетке этой таблицы, расположенной на пересечении строки, проходящей через элемент , и столбца, проходящего через элемент , следует записать композицию элементов и .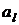

Часто алгебраическую операцию называют внутренним законом композиции.

Определение 2. Пусть заданы множество X с бинарной алгебраической операцией °, и любое его непустое подмножество X₁. Если "a,b'X₁ a°b тоже принадлежит X₁ ,то множество X₁ называют устойчивым относительно данной бинарной алгебраической операции, а саму бинарную алгебраическую операцию на X₁ называют индуцированной.

Определение 3. Пусть на множестве Х задана бинарная алгебраическая операция ° (дальше для краткости просто операция °). Элемент hÎХ называется нейтральным относительно операции °, если x°h=h°x=x "xÎX.

Примеры.

1) В операции умножения на множестве целых чисел Z роль нейтрального элемента играет 1.

2) На множестве 2Z нет нейтрального элемента относительно умнажения.

Теорема 1.Относительно любой алгебраической операции существует не более одного нейтрального элемента.

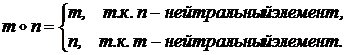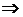Доказательство (от противного). Пусть m и n нейтральные элементы относительно операции ° на X, причем m¹n. Тогда по определению нейтрального элемента: Þ m=n.

Определение 4. Алгебраическая оперция °, заданная на множестве X, называется ассоциативной, если "a,b,cÎX выполняется: (a°b) °c=a°(b°c).

Теорема 2. Пусть на множестве Х задана ассоциативная операция °, тогда:

(a₁°…°a_i) °(a_i+1°…°a_n )= a₁°…°a_n

Доказательство индукцией (по числу элементов во второй скобке):

1) Если n – i=1, то равенство верно по определению.

2) Если n - i=k, то будем считать утверждение верным.

3) Докажем верность для n - i=k+1.

(a₁°…°a_i)°(a_i+1°…°a_n )= (a₁°…°a_i)°((a_i+1°…°a_n-1 ) °a_n ) так как операция ° ассоциативна, то по-другому расставим скобки и воспользуемся индуктивным предположением

(a₁°…°a_i)°((a_i+1°…°a_n-1 )°a_n )= =((a₁°…°a_i)°(a_i+1°…°a_n-1 )) °a_n = a₁°…°a_n .

Следствие. Пусть на множестве Х задана ассоциативная операция °. Тогда композиция конечного числа элементов множества Х не зависит от распределения скобок, указывающих на порядок производимых действий.

Определение 5. Пусть на множестве Х задана операция °, n – нейтральный элемент и x,y —некоторые элементы из множества Х. Элемент y называется симметричным элементу x относительно операции °, если x°y=y°x=n. Если для элемента x есть симметричный, то он называется симметризуемым.

Примеры:

1) На множестве целых чисел, операция +, n=0, симметричный элемент элементу — противоположный .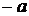

2) Множество матриц над полем P_n, E — единичная матрица (нейтральный элемент при умножении). Симметричный элемент существует тогда, когда матрица обратима, т.е ее определитель не равен нулю.

Теорема 3. Пусть на множестве X задана ассоциативная операция ° и n — нейтральный элемент. Тогда "xÎX существует не более одного симетричного элемента.

Докозательство (от противного).

Пусть для некоторого элемента x существует несколько симметричных элементов, например: y,z. Тогда рассмотрим композицию: y°x°z=y°(x°z)=y°n=y, с другой стороны y°x°z=(y°x)°z)=n°z=z Þ y=z.