Определитель произведения квадратных матриц.

Теорема. Пусть А и В — две квадратные матрицы порядка n. Тогда определитель их произведения равен произведению определителей, т.е.

| AB | = | A| | B |.

¢ Пусть A = (a_ij)_{n x n} , B = (b_ij)_{n x n} . Рассмотрим определитель d_2n порядка 2n

A

||

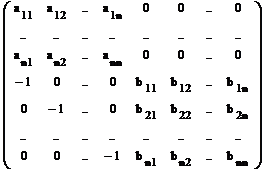
d_2n =

||

B

d_2n = | A | | B | (-1) ^{1 + ... + n + 1 + ... + n} = | A | | B |.

Если мы покажем, что определитель d_2n равен определителю матрицы С=АВ, то теорема будет доказана.

В d_2n проделаем следующие преобразования: к 1 строке прибавим (n+1) строку, умноженную на а₁₁; (n+2) строку, умноженную на а₁₂ и т.д. (2n) строку, умноженную на а_1n . В полученном определителе первые n элементов первой строки будут нулями, а n других элементов станут такими:

a₁₁b₁₁ + a₁₂b₂₁ + ... + a_1nb_n1 = c_11;

a₁₁b₁₂ + a₁₂b₂₂ + ... + a_1nb_n2 = c_12;

_...

a₁₁b_1n + a₁₂b_2n + ... + a_1nb_nn = c_1n.

Аналогично получаем нули во 2, …, n строках определителя d_2n , причем последние n элементов в каждой из этих строк станут соответствующими элементами матрицы С. В результате, определитель d_2n преобразуется в равный ему определитель:

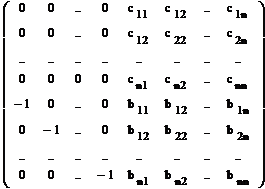
d_2n = | C | (-1) ^{1 + ... + n + ... + 2n} = |AB|. £

Следствие. Определитель произведения конечного числа квадратных матриц равен произведению их определителей.

¢ Доказательство проводится индукцией: | A₁ ... A_i+1 | = | A₁... A_i | | A_i+1 | = ... = = | A₁| ... | A_i+1 | . Эта цепочка равенств верна по теореме. £

Обратная матрица.

Пусть A = (a_ij)_{n x n} квадратная матрица над полем Р.

Определение 1. Матрицу А будем называть вырожденной, если ее определитель равен 0. Матрицу А будем называть невырожденной в противном случае.

Определение 2. Пусть А Î P_n. Матрицу В Î P_n будем называть обратной к А, если АВ = ВА=Е.

Теорема (критерий обратимости матрицы).Матрица А обратима тогда и только тогда, когда она невырожденная.

¢ Пусть А имеет обратную матрицу. Тогда АА^-1 = Е и, применяя теорему об умножении определителей, получаем | A | | A^-1 | = | E | или | A | | A^-1 | = 1. Следовательно, | A | ¹ 0.

Пусть, обратно, | A | ¹ 0. Надо показать, что существует матрица В такая, что АВ = ВА = Е. В качестве В возьмем такую матрицу:

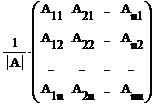
В = ,

где А_ij — алгебраическое дополнение к элементу а_ij . Тогда

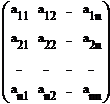
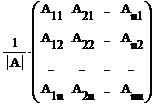
АВ =

Следует заметить, что в результате получится единичная матрица (достаточно воспользоваться следствиями 1 и 2 из теоремы Лапласа § 6), т.е. АВ = Е. Аналогично показывается, что ВА = Е. £

Пример. Для матрицы А найти обратную матрицу, или доказать, что ее нет.

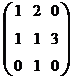
А =

det A = -3 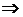обратная матрица существует. Теперь считаем алгебраические дополнения.

А₁₁ = -3 А₂₁ = 0 А₃₁ = 6

А₁₂ = 0 А₂₂ = 0 А₃₂=-3

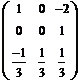
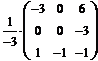А₁₃ = 1 А₂₃ = -1 А₃₃ = -1

Итак, обратная матрица имеет вид: В = =

Алгоритм нахождения обратной матрицы для матрицы А.

1. Вычисляем det A.

2. Если он равен 0, то обратной матрицы не существует. Если det A не равен 0, считаем алгебраические дополнения .

3. Ставим алгебраические дополнения на соответствующие места.

4. Все элементы получившейся матрицы делим на det A.

Упражнение 1. Выяснить, однозначна ли обратная матрица.

Упражнение 2. Пусть элементы матрицы А — целые рациональные числа. Будут ли элементы обратной матрицы целыми рациональными числами?

Системы линейных уравнений.

Определение 1. Уравнение вида a₁x₁+ ....+a_nx_n=b , где a, ... ,a_n — числа; x₁, ... ,x_n — неизвестные, называется линейным уравнением с n неизвестными.

s уравнений с n неизвестными называется системой s линейных уравнений с n неизвестными, т.е.

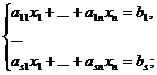
(1)

Матрица А, составленная из коэффициентов при неизвестных системы (1), называется матрицей системы (1).

.

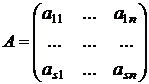Если к матрице А добавить столбец свободных членов, то получим расширенную матрицу системы (1).

X = — столбец неизвестных.

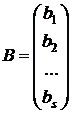— столбец свободных членов.

В матричном виде система имеет вид: AX=B (2).

Решением системы (1) называют упорядоченный набор n чисел (α₁ ,…, α_n) таких, что если сделаем подстановку в (1) x₁ = α₁, x₂ = α₂ ,…, x_n = α_n , то мы получим числовые тождества.

Определение 2. Систему (1) называют совместной, если она имеет решения, и несовместной в противном случае.

Определение 3. Две системы называют эквивалентными, если множества их решений совпадают.

Существует универсальный способ решения системы (1) — метод Гаусса (метод последовательного исключения неизвестных), см. [1], стр.15.

Рассмотрим более подробно случай, когда s = n. Существует метод Крамера решения таких систем.

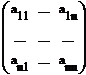Пусть d = det ,

d_j — определитель d, в котором j–тый столбец заменен столбцом свободных членов.

Теорема (правило Крамера). Если определитель системы d ¹ 0, тогда система имеет единственное решение, получающееся по формулам:

x₁ = d₁ / d …x_n = d_n / d

¢Идея доказательства заключается в том, чтобы переписать систему (1) в форме матричного уравнения. Положим

X = , B =

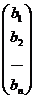
и рассмотрим уравнение AX = B (2) с неизвестной матрицей-столбцом X. Так как A, X, B — матрицы размеров n x n, n x 1, n x 1 соответственно, то произведение прямоугольных матриц АХ определено и имеет те же размеры, что и матрица В. Таким образом, уравнение (2) имеет смысл.

Связь между системой (1) и уравнением (2) заключается в том, что 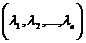является решением данной системы тогда и только тогда, когда

столбец есть решение уравнения (2).

Действительно, это утверждение означает выполнение равенства

=

= .

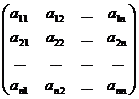
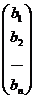
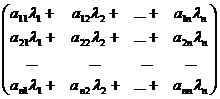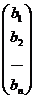Последнее равенство, как равенство матриц, равносильно системе равенств

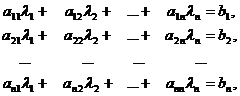
которое означает, что 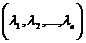— решение системы (1).

Итак, решение системы (1) сводится к решению матричного уравнения (2). Так как определитель d матрицы А отличен от нуля, она имеет обратную матрицу А^-1. Тогда АХ = В 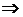А^-1(АХ) = А^-1В 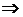(А^-1А)Х = А^-1В 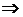ЕХ = =А^-1В 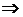Х = А^-1В (3). Следовательно, если уравнение (2) имеет решение, то оно задается формулой (3). С другой стороны, А(А^-1В) = (АА^-1)В = ЕВ = В.

Поэтому Х = А^-1В есть единственное решение уравнения (2).

Так как ,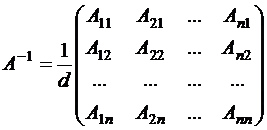

где А_ij — алгебраическое дополнение элемента a_ij в определителе d, то

= ,

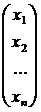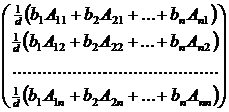откуда 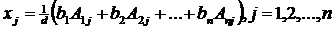(4).

В равенстве (4) в скобках написано разложение по элементам j-го столбца определителя d_j, который получается из определителя d после замены в нем

j-го столбца столбцом свободных членов. Поэтому, x_j = d_j / d. £

Следствие. Если однородная система n линейных уравнений от n неизвестных имеет ненулевое решение, то определитель этой системы равен нулю.

ТЕМА 3. Многочлены от одной переменной.