Теорема (об ассоциативности произведения матриц).

Пусть А, В, С — матрицы над числовым полем Р такие, что определено произведение АВ и ВС. Тогда имеют смысл произведения (АВ)С, А(ВС) и верно равенство (АВ)С = А(ВС).

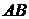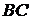¢ Пусть A = (a_ij)_{m x n} , B = (b_ij)_{n x p} , С = (с_ij)_{р x s} . Они подходящих размеров, чтобы было определено и . Введем обозначения АВ = (d_ij)_{m x p} , BC = (l_ij)_{n x s} , A(BC) = (f_ij)_{m x s} , (AB)C = (r_ij)_{m x s} . Матрицы A(BC) и (AB)C одинаковых размеров. Требуется проверить, что f_ij = r_ij . Выразим f_ij и r_ij через элементы матриц А, В, С:

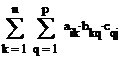
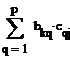
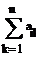
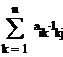
f_ij = = = . _,

.

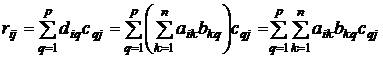Полученные суммы отличаются лишь порядком суммирования, что не влияет на результат (по замечанию 2). £

Определение. Произведение нескольких матриц определим индуктивно, т.е. если имеем k матриц, то их произведение определим следующим образом: (A₁, ... , A_k-1) A_k

Упражнение. Доказать, что в произведении нескольких матриц скобки можно расставлять как угодно.

Указание. Воспользоваться ассоциативностью.

Теорема 2. Пусть A = (a_ij)_{m x n} . Тогда AE_n = E_mA = A, где Е — единичная матрица подходящего размера.

¢ Доказательство проводится непосредственной проверкой равенства:

=

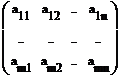
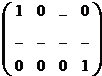
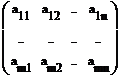
Аналогично доказывается, что E_mA = А . £

Теорема 3. Пусть A = (a_ij)_{m x n} . Тогда АО_{n x s} = O_{m x s} , где О — нулевая матрица подходящего размера.

¢ Произведение таких матриц будет матрицей размером m x s. Каждый элемент, очевидно, будет равен 0. £

Теорема 4 (дистрибутивность умножения матриц относительно сложения матриц).

(А + В)С = АС + ВС, где С — матрица подходящего размера, и — матрицы одинаковых размеров.

¢ Пусть A = (a_ij)_{m x n} , B = (b_ij)_{m x n} , С = (с_ij)_{n x p} . Понятно, что (А + В)С и АС + ВС одинаковых размеров. Чтобы доказать их равенство, надо показать, что на одних и тех же местах стоят одни и те же элементы.

Следующее равенство доказывает теорему:

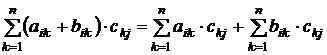
элемент на элемент элемент на

позиции 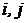на позиции позиции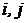

матрицы 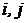матрицы матрицы

¢

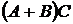
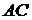
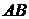Транспонирование матриц.

Определение 1. Пусть A = (a_ij)_{m x n} . Транспонирование матрицы — это такое ее преобразование, при котором строка с номером i записывается в столбец с тем же номером.

Обозначение: А^t , А^tr , А'.

Пример:

, то .

Теорема 5.Имеют место следующие равенства:

1. (А^t)^t = A.

2. (αA + βB)^t = αA^t + βB^t.

3. (AB)^t = В^tА^t .

Причем, А и В — матрицы подходящих размеров, α и β — любые числа.

¢ 1. А = (а_ij)_{m x n}

(A)^t = (а_ji)_{n x m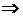} (А^t)^t = A.

2. Доказать самостоятельно.

3. Пусть имеем А = (а_ij)_{m x n} и B = (b_ij)_{n x s} . Тогда A^t = ( _ij)_{n x m} , B^t = =( _ij)_{s x n}, AB = (c_ij)_{m x s}, B^tА^t = (d_ij)_{s x m} , (AB)^t = ( _ij)_{s x m}.

Матрица В^tA^t и (AB)^t одинаковых размеров, и чтобы доказать, что В^tA^t = (AB)^t , надо показать, что на одинаковых местах стоят одинаковые элементы.

.

Мы получили, что на позиции ij у матрицы В^tA^t и матрицы (AB)^t стоит один и тот же элемент. £

Определение 2. Матрица А называется симметрической, если А^t = А, и кососимметрической, если А^t = -А.

Пример. Симметрическая матрица:

кососимметрическая матрица:

Упражнение. Будет ли произведение симметрических (кососимметрических) матриц симметрической (кососимметрической) матрицей? Если будет, доказать. Если не будет, привести пример.

Перестановки.

Пусть X — непустое множество элементов произвольной природы, так как природа элементов для нас несущественна, то в случае конечного множества считаем X = .

Определение 1. Любое упорядоченное расположение элементов множества X называется перестановкой множества X.

Пример:

Если X = , то (2,5,3,4,1) - перестановка множества X.

Перестановку элементов множества X обозначают , причем среди (i = 1,2,…, n) нет равных.

Определение 2. Две перестановки множества X называются равными, если у них на одинаковых местах стоят одинаковые элементы.

Теорема 1.Число различных перестановок множества из n элементов равно n!

◄ Докажем эту теорему индукцией по числу . При 1 имеется одна перестановка, т.е. 1!.

Пусть >1 и число различных перестановок, которые можно составить из заданных ( ) элементов, равно . Всякая перестановка данных элементов с фиксированным первым числом а имеет вид:

,

где произвольная перестановка оставшихся ( ) элементов. По индуктивному предположению число таких перестановок равно .В качестве а, можно взять любой из данных элементов, поэтому число различных перестановок заданных элементов равно сумме n слагаемых, каждое из которых есть , т.е. n!►

Определение 3. Будем говорить, что в перестановке чисел два числа образуют инверсию если > , но i < j. В противном случае образуют порядок.

Пример:

В перестановке (1 3 4 2) инверсии: 4,2 ; 3,2 , а остальные пары образуют порядок.

Определение 4. Количество пар чисел, образующих инверсию в перестановке, называют числом инверсий данной перестановки. Отображение X X будем называть преобразованием множества X.

Пусть множество X состоит не менее чем из двух элементов X.

Определение 5. Преобразование множества Х называют транспозицией элементов и , если , , .Такое преобразование обозначают .

Определение 6. Перестановку называют четной, если число инверсий в ней четно, и нечетной в противном случае.

Теорема 2.Однократное применение транспозиции к перестановке изменяет ее характер четности на противоположный.

◄ Пусть имеется перестановка . Применим к ней транспозицию , получим . Рассмотрим несколько случаев:

1. Пусть и стоят рядом. Если и в образуют инверсию, то образуют порядок. Поэтому характер четности изменяется на противоположный, ибо число инверсий изменяется на единицу.

2. Пусть и не стоят рядом . От к можно перейти следующим способом: менять с рядом стоящим элементом дойти до и перегнать на место . Всего нам придется применить S+1+S=2S+1 транспозиций соседних чисел, где число элементов между и , поэтому характер четности перестановок и различны.►

Следствие.При 2 число четных перестановок равно числу нечетных перестановок и равно .

◄ Пусть число четных перестановок равно S, нечетных — T. Если к каждой четной перестановке мы применим транспозицию двух элементов, мы превратим их в нечетные S , аналогично наоборот T T=S

=S+T =2S

S=T= .►

Теорема 3.Пусть даны две различные перестановки одних и тех же чисел, тогда существует последовательность транспозиций переводящих первую перестановку во вторую.

◄ Пусть

есть произвольные перестановки из n чисел. Если , то применив к перестановке транспозицию получим перестановку n чисел вида

Если , то к перестановке применим транспозицию .В результате получим перестановку . Продолжаем этот процесс получаем требуемое.►

Замечание.В доказательстве теоремы содержится алгоритм нахождения последовательности транспозиций, переводящих одну перестановку в другую.

Пример:

(1, 2, 3, 4)

(3, 1, 4 ,2)

(1,2,3,4) (3,2,1,4) (3,1,2,4) (3,1,4,2).

(6) (7)

Такая последовательность транспозиций не однозначна (это может быть не самый короткий путь перехода от одной перестановки к другой).

Подстановки.

Пусть X X , при этом если — биективно, то часто называют подстановкой. Мы ограничимся случаем, когда число элементов конечно, и равно n .

X = , тогда отображение можно записать в виде таблицы:

Если подстановка, тогда — перестановка. Запись отображения в виде таблице (1) позволяет хорошо перемножать отображения.

Пример.

Теорема 1.Всякая подстановка конечного множества, содержащая не менее двух элементов, может быть представлена в виде произведения транспозиций.

◄ Пусть имеем .Согласно теореме 3 предыдущего параграфа, существует последовательность транспозиций переводящая первую перестановку во вторую, пусть это будет следующая последовательность транспозиций . Тогда очевидно, что , ибо отображения действуют на одном и том же множестве и результат их действия одинаков. ►

Замечание. Разложение подстановки в произведение транспозиций, вообще говоря, неоднозначно.

Теорема 2.Характер четности числа сомножителей во всех разложениях подстановки в произведение транспозиций один и тот же.

◄ Пусть подстановка вида (1) разлагается в произведение k транспозиций. Это значит, что существует последовательность k транспозиций, переводящая перестановку (2) в перестановку (3). Однократное применение транспозиции меняет характер четности перестановки, поэтому k — четное число тогда и только тогда, когда перестановки(2) и (3) одного характера четности. Это и доказывает теорему.►

Определение 1. Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетная в противном случае.

Упражнение. Число четных подстановок равно числу нечетных и равно .

Определители и их свойства.

Пусть А — некоторая матрица размеров n x n над полем Р.

A =

Возьмем из каждой строки и каждого столбца матрицы по одному элементу . Тогда (i_{1 ..........}i_n ) (1) будет некоторой перестановкой чисел 1,2, … , n. Возьмем произведение этих элементов и умножим на (-1) ^t , где t — число инверсий в перестановке (1). Получим (-1) ^t (2). Это произведение (2) принято называть членом определителя матрицы А.

Определение. Определителем (детерминантом) матрицы А назовем сумму всех членов определителя матрицы А.

Определитель матрицы А обозначается одним из символов: | A | , det A .

Замечание. Количество членов определителя матрицы А равно n!

Примеры:

1) n=1; A = (a₁₁) . Определитель матрицы равен a₁₁.

2) n=2; A = , тогда det A = а₁₁а₂₂ – а₁₂а₂₁.

3) n=3; A = , тогда det A = a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ –

– a₁₃a₂₂a₃₁ – a₁₂a₂₁a₃₃ – a₁₁a₂₃a₃₂.

Если , считать определитель по определению становится уже громоздким. Для того, чтобы считать определитель, нужно использовать его свойства.

Свойства определителей.

1) Определитель матрицы не изменяется при ее транспонировании, т.е.

det A = det A^t.

2) Если у матрицы поменять местами две строки, то ее определитель изменит знак на противоположный.

3) Определитель матрицы с нулевой строкой равен 0.

4) Определитель матрицы, содержащий две равные строки, равен 0.

5) Постоянный множитель всех элементов какой-нибудь строки определителя можно выносить за знак определителя.

6) Определитель матрицы, содержащей две пропорциональные строки,

равен 0.

7)

d = = + ,

|| ||

d₁ d₂

где a_ik=b_ik+c_ik , где к = 1, ... , n.

Определитель матрицы d, у которой i-тая строка представлена в виде a_ik=b_ik+c_ik , где к = 1, … , n, равен сумме определителей d₁ и d₂ , которые отличны от d i - той строкой, а именно, у d₁ i–тая строка b_ik , у d₂ - c_ik, .

8) Если в определителе к какой–нибудь строке прибавить другую строку, умноженную на произвольное число, то определитель при этом не изменится.

¢ Доказательство всех этих свойств основано на определении определителя и несложных наблюдениях.

Докажем, например, свойство 1.

Пусть А = (a_ij), A^t = (b_ij) — транспонированная к А матрица, т.е.

b_ij = a_ji. (3)

Требуется доказать, что | A | = | A^t |.

Рассмотрим произвольный член определителя | A^t | : (-1)^t (4),

где t — число инверсий в перестановке j₁, j₂, …, j_n (5). Учитывая (3), перепишем (4) в виде (-1)^t = (-1)^t (6). Так как (5) — перестановка из n чисел, то правую часть (6) можно переписать следующим образом: (-1)^t = (-1)^t (7). Это равносильно тому, что подстановка (8) записывается в виде (9).

Из (6) и (7) получаем (-1)^t = (-1)^t (10).

Правая часть равенства (10) есть с точностью до знака член определителя | A |. Покажем, что перестановка l₁, l₂, …, l_n (11) имеет тот же характер четности, что и перестановка (5).

Действительно, перестановка (11) имеет ту же четность, что и подстановка (9), равная подстановке (8). Четность подстановки (8) совпадает с четностью обратной к ней подстановки (12). Наконец, подстановка (12) имеет ту же четность, что и перестановка (5). Итак, если k — число инверсий в перестановке (11), то с учетом (10) имеем (-1)^t = (-1)^k , т.е. член определителя |A^t|, соответствующий перестановке (5), равен члену определителя |A|, соответствующий перестановке (11). Отсюда и следует равенство определителей |A| и |A^t|.

Докажем теперь свойство 7.

Если (-1)^t есть произвольный член определителя (напомним, что t — число инверсий в перестановке j₁,..., j_i, ..., j_n), то

d = å(-1) ^t = å(-1) ^t =

= å(-1) ^t + å(-1) ^t = d₁ + d₂ . £

Замечание. Так как при транспонировании матрицы столбцы становятся строками, то из свойства 1 следует, что все утверждения, доказанные нами для строк определителя, верны и для его столбцов.

Пример 1. det = det = 1 · 1 · 2 · 7 = 14.

Пример 2. det = а₁₁… а_nn.