Теорема (о делении с остатком).
Для любых a, bÎZ; b ¹ 0 существует единственная пара q, rÎZ такая, что a = bq+r, 0£ r<|b|.
Доказательство: Рассмотрим множество M = {a – bq, qÎZ}. Очевидно, что M∩{N, 0}¹Ø.
В любом таком множестве $ наименьшее r. Очевидно, что |b|>r ≥0.
Докажем единственность.
Пусть ещё a = bq1 + r1. Тогда вычитанием из первого второе получим
0 = b(q – q1) + r – r1. Отсюда следует, что r – r1 кратно b, но |r – r1|<|b|.
Следовательно, r – r1 = 0, а поэтому и q – q1 = 0.
Упражнение.Доказать теорему о делении с остатком геометрически (использовать геометрическую интерпретацию чисел).
Следствие из теоремы.
b делит a тогда и только тогда, когда r = 0 (b|a Û r = 0);
r называют остатком, а q – частным.
Построение комплексных чисел.
Уравнение x2+1=0 не имеет решения в области действительных чисел. Построение комплексных чисел попутно решает задачу о расширении множества действительных чисел до такого множества, чтобы уравнение x2+1=0 имело решение.
В качестве исходного материала для построения комплексных чисел возьмём множество точек плоскости. Будем их обозначать z1, z2,…, zn. Если на плоскости выбрана Декартова система координат, то между точками на плоскости и множеством пар чисел (a, b), где a и bÎR, можно установить взаимно однозначное соответствие, т.е.
z  (a, b), где
(a, b), где  – равно по определению.
– равно по определению.
Введём операции сложения и умножения точек плоскости.
Определение 1.Под суммой точек z1=(a, b) и z2=(c, d) будем понимать точку z = z1+z2  (a+c, b+d).
(a+c, b+d).
Определение 2.Под произведением точек z1=(a, b) и z2=(c, d) будем понимать точку z = z1z2  (ac–bd, ad+bc)
(ac–bd, ad+bc)
Теорема 1.
1) z1+z2=z2+z1 — коммутативность сложения;
2) (z1+z2)+z3= z1+(z2+z3) — ассоциативность сложения;
3) z1z2= z2z1 — коммутативность умножения;
4) (z1z2)z3= z1(z2z3) — ассоциативность умножения;
5) (z1+z2)z3 = z1z3+z2z3 — дистрибутивность умножения относительно сложения.
Для любых z1, z2, z3.
Доказательство утверждений 1) – 5) сводится к подсчёту правой и левой частей и проверке их равенства. Докажем, например, 3) :
z1z2 = (ac–bd, ad+bc) = (ca–db, cb+da) = z2z1 Þ z1z2= z2z1.
Введённые операции сложения и умножения обладают теми же свойствами, что и числа.
Определение 3.Под разностью точек z1=(a, b) и z2=(c, d) будем понимать точку z = (x, y) такую, что z2+ z = z1, т.е.
z2+z = z1 Û  Þ
Þ 
z1–z2 = (a – c, b – d).
Определение 4.Пусть z1 = (a, b), z2 = (c, d), z2 ¹ (0, 0).
Частным двух точек z1 и z2 называют точку z = (x, y) такую, что z2z = z1, т.е.
 Þ
Þ 
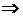
x =  ; y =
; y =  .
.
Точка с координатами (0, 0) играет роль нуля. Роль единицы играет точка с координатами (1, 0). Противоположной точке z1 = (a, b) будет точка z2 = (–a, –b).
Упражнение. Найти обратную точку для точки z2 = (c, d)≠(0,0).
Множество точек плоскости с так введёнными операциями сложения, умножения, вычитания и деления называют множеством комплексных чисел и обозначают C.
Точки с координатами (a, 0) на оси Ox и
(a, 0)+(b, 0) = (a+b, 0), (a, 0)(b, 0) = (ab, 0).
По своим свойствам множество таких точек ничем не отличаются от R, поэтому будем отождествлять (a, 0) и a. После этого отождествления множество C содержит R (C É R).
В множестве C имеет решение уравнение x2+1=0.
Это точка с координатами (0, 1): (0, 1) (0, 1) = (–1, 0).
Точка (0, 1) — обозначается i и называется мнимой единицей. Очевидно, что
(a, b) = (a, 0)+(0, b) = a+(b, 0)(0, 1) = a+bi, где a+bi — алгебраическая форма комплексного числа.
Замечание. Введенные ранее операции над комплексными числами приспособлены к алгебраической форме записи комплексного числа. Например, для умножения двух чисел имеем:
(a+bi)(c+di) = ac+adi+cbi+bdi2=(ac–bd)+i(ad+bc).
Пусть z = a+bi, тогда:
a = Re z — действительная часть комплексного числа,
b = Im z — мнимая часть комплексного числа.
Множество точек плоскости может служить геометрическим изображением комплексных чисел.
Определение 5.Два комплексных числа равны, если равны их мнимые и действительные части (следует из геометрической интерпретации комплексных чисел).
Два комплексных числа называют сопряжёнными, если их действительные части равны, а мнимые — противоположны (сопряжённое к z обозначаем через  ).
).
Упражнение 1.Сумма и произведение двух комплексных чисел z и  (сопряжённых) — действительное число.
(сопряжённых) — действительное число.
Теорема 2.
Справедливы следующие соотношения:
1)  =
=  +
+  ;
;
2)  =
=  –
–  ;
;
3)  =
= 
 ;
;
4)  =
=  .
.
Доказательство.
Доказательство 1) – 4) однообразно и сводится к подсчёту левой и правой частей и их сравнению. Например: z1=a+bi, z2=c+di. Докажем
1)  =
=  +
+  . По определению
. По определению
 = a-bi ;
= a-bi ;  =c-di и
=c-di и
 = (a+c)–(bi+di),
= (a+c)–(bi+di),
 +
+  = (a–bi)+(c–di) = (a+c)–(bi+di).
= (a–bi)+(c–di) = (a+c)–(bi+di).
Значит  =
=  +
+  .
.
§3. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА
КОМПЛЕКСНОГО ЧИСЛА.
Пусть z = a+bi , полагаем r 
 =|z|, r — модуль комплексного числа z.
=|z|, r — модуль комплексного числа z.
a+bi = 
 , положим
, положим
 = cos
= cos  и
и  = sin
= sin  .
.
Пусть z¹0, тогда угол j определен однозначно с точностью до 2pk. Если 0£j£2p, то он определен однозначно. Угол j называют аргументом комплексного числа z, r и j — полярные координаты точки.
Из тригонометрии мы знаем как искать j, если известно a и b.
Если r=0, то j может быть любой, то есть аргумент нуля не определён; r¹0, то аргумент определен с точностью до 2πk.
z = r(cosj+i sinj) (1)
Назовем выражение (1) тригонометрической формой комплексного числа.
Если два комплексных числа равны, то их модули равны, а их аргументы, вообще говоря, отличаются на 2pk.
Теорема 1.
Пусть z1 = r1 (cosj1+i sinj1), z2 = r2 (cosj2+i sinj2). Тогда:
1) z1z2 = r1r2(cos(j1+j2)+i sin(j1+j2))
 |
(модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов);
2)
(модуль частного комплексных чисел равен частному модулей, а аргумент – разности аргументов).
Доказательство:
Докажем 1).
z1z2 = r1r2(cosj1cosj2– sinj1sinj2+i(sinj1cosj2+cosj1sinj2)) = =r1r2cos(j1+j2)+i sin(j1+j2)).
Аналогично с частным.
Следствие 1.
Пусть z = r (cosj+i sinj), тогда z  =
=  (cos(–j)+i sin(–j)).
(cos(–j)+i sin(–j)).
Доказательство:
z  =
=  =
=  =
=  =
=  (cos(–j)+i sin(–j)).
(cos(–j)+i sin(–j)).
Следствие 2(формула Муавра).
Пусть z = r (cosj+i sinj). Тогда zn = rn(cos(nj)+i sin(nj)) для любого nÎZ.
Доказательство:
Если n — натуральное, то формула Муавра следует из правила умножения комплексных чисел в тригонометрической форме.
Если n — отрицательное, то можно представить zn = (z -1)-n и применить следствие (1) и доказанную формулу Муавра для nÎN.
