Контрольная работа №1 «Линейная алгебра. Аналитическая геометрия»
1) Даны матрицы: 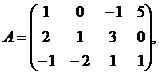
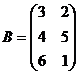 ,
, 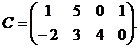
Найти 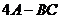 .
.
2) Дана матрица 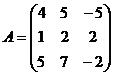 . Найти обратную к ней матрицу
. Найти обратную к ней матрицу 
3) Решить системы линейных уравнений методом Жордана – Гаусса:
а) 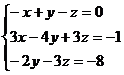 b)
b) 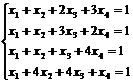
4) Даны векторы 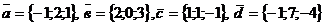 .
.
a)Доказать, что вектора 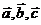 образуют базис и найти разложение вектора
образуют базис и найти разложение вектора 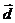 по этому базису.
по этому базису.
b) Найти скалярное произведение векторов 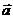 и
и 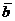 .
.
c) Найти векторное произведение векторов 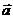 и
и 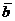 .
.
d) Найти смешанное произведение векторов 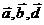 .
.
5) Даны координаты вершин треугольника, A(8;2), B(-8;-10), C(-1;14). Найти:
a) длину стороны AB;
b) общие уравнения сторон AB и BC;
c) величину угла B;
d)длину и уравнение высоты, опущенной из вершины 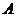 ;
;
e) площадь треугольника 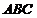 ;
;
f) уравнение прямой, проходящей через точку 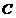 параллельно стороне
параллельно стороне 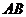 .
.
6) Даны четыре точки A(-2,5;-1;-1), B(0,5;-2;1), C(-1,5;-3;-1), M(3;-3;-1). Найти:
a)уравнение плоскости a, проходящей через три точки A, B, C;
b)каноническое уравнения прямой AB;
c)уравнение и длину высоты, опущенной из вершины М на грань 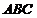 ;
;
d) объем пирамиды АВСМ.
7) Дано уравнение кривой второго порядка: 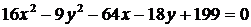 .
.
Привести его к каноническому виду, определить вид кривой, указать её параметры (для эллипса и гиперболы – центр, вершины, полуоси, фокусы, а для гиперболы и асимптоты. Для параболы указать координаты вершины, координаты фокуса, величину параметра p, уравнение директрисы). Изобразить кривую на координатной плоскости.
Контрольная работа №2 «Введение в анализ.
Дифференциальное исчисление функции одной и нескольких переменных»
1) Вычислить пределы, не пользуясь правилом Лопиталя:
a) 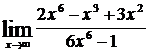 ; b)
; b) 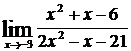 ; c)
; c) 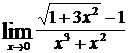 ;
;
d) 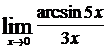 ; e)
; e) 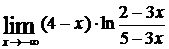
2)Исследовать функции на непрерывность. Классифицировать точки разрыва.
a) 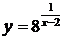 ; b)
; b) 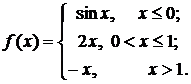
3) Найти производные 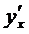 для следующих функций:
для следующих функций:
a) 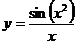 ; b)
; b) 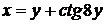 ; c)
; c) 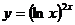 ; d)
; d) 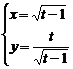
4) Найти уравнения касательной и нормали к графику функции 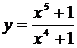
в точке x0=1.
5) С помощью методов дифференциального исчисления построить график функции 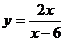 .
.
6) Найти наибольшее и наименьшее значения функции 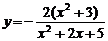
на отрезке 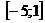 .
.
7) Даны функция 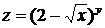 и точки A(1;3), B(0,97;3,02). Вычислить:
и точки A(1;3), B(0,97;3,02). Вычислить:
a)значение функции 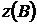 ;
;
b) 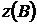 с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
c) cоставить уравнения касательной плоскости и нормали к поверхности 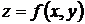 в точке A.
в точке A.
8) Даны функция 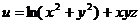 , точка М(1;-1;2) и вектор
, точка М(1;-1;2) и вектор 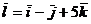 .
.
Найти:
a) градиент данной функции в точке М;
b) производную функции в точке М по направлению вектора 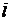 .
.
9) Дана функция 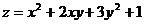 . Найти:
. Найти:
a) экстремум данной функции;
b) наибольшее и наименьшее значения функции в области 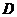 , ограниченной линиями:
, ограниченной линиями: 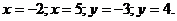
Типовой разбор варианта контрольной работы
Контрольная работа №1
1)Даны матрицы: 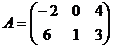 ,
, 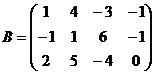 ,
, 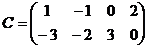 .
.
Найти 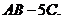
Решение:
Матрица А имеет размерность 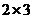 , матрица В размерность
, матрица В размерность 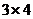 . Т.к. число столбцов первой матрицы равно числу строк второй матрицы, то данные матрицы можно перемножить. В результате получится некоторая матрица D, имеющая размерность
. Т.к. число столбцов первой матрицы равно числу строк второй матрицы, то данные матрицы можно перемножить. В результате получится некоторая матрица D, имеющая размерность 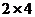 .
.
Найдем элементы матрицы D:
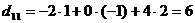 ;
; 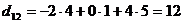 ;
; 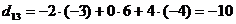 ;
; 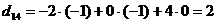 ;
;
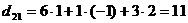 ;
; 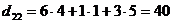 ;
; 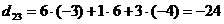 ;
; 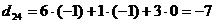 .
.
Тогда 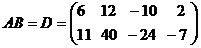 .
.
По правилу умножения матрицы на число 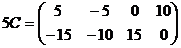
Найдём 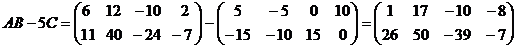 .
.
2)Дана матрица: 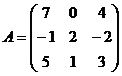 . Найти обратную к ней матрицу
. Найти обратную к ней матрицу 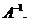
Решение:
Вычислим определитель матрицы А методом треугольников:
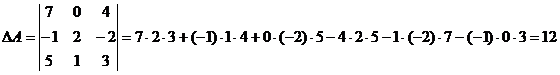
Т.к. 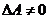 , то обратная матрица может быть найдена. Найдём алгебраические дополнения для всех элементов матрицы А:
, то обратная матрица может быть найдена. Найдём алгебраические дополнения для всех элементов матрицы А:
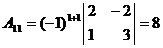 | 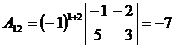 | 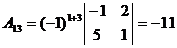 |
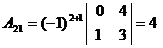 | 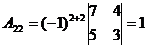 | 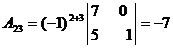 |
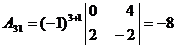 | 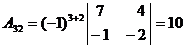 | 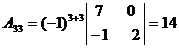 . . |
Составим присоединённую матрицу 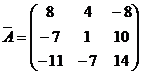
Обратная матрица 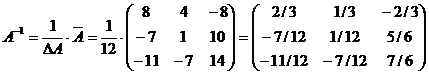
Для проверки, правильности вычисления 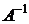 , найдём
, найдём
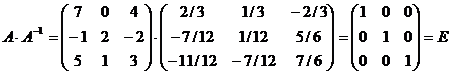
3) Решить систему методом Жордана – Гаусса:
a) 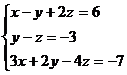
Решение:
Рассмотрим расширенную матрицу системы: 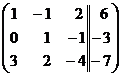 . Приведём её к верхне- треугольному виду.
. Приведём её к верхне- треугольному виду.
Из 3-ей стоки вычтем 1-ю строку, умноженную на 3: 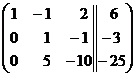 .
.
Разделим 3-ю строку на 5: 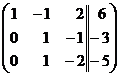
Вычтем из 3-ей строки 2-ю строку: 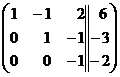 и разделим 3-ю строку
и разделим 3-ю строку
на (-1): 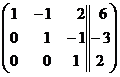 . Мы привели матрицу к верхнее- треугольному виду.
. Мы привели матрицу к верхнее- треугольному виду.
Заменим исходную систему системой, полученной путём преобразования матрицы и найдем значения переменных: 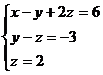
Из 2-го уравнения при 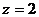 получим
получим 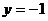 .Подставляя значения y и z в 1-ое уравнение найдем значение
.Подставляя значения y и z в 1-ое уравнение найдем значение 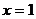 .Тогда решение системы может быть представлнно в виде матрицы-столбца:
.Тогда решение системы может быть представлнно в виде матрицы-столбца: 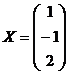 .
.
b) 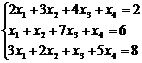
Решение:
Рассмотрим расширенную матрицу системы: 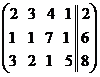 . Приведём её к верхнее треугольному виду.
. Приведём её к верхнее треугольному виду.
Поменяем местами 1-ю и 2-ю строки: 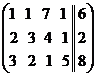 . Из 2-ой стоки вычтем 1-ю строку, умноженную на 2, из 3-ей стоки вычтем 1-ю строку, умноженную на 3:
. Из 2-ой стоки вычтем 1-ю строку, умноженную на 2, из 3-ей стоки вычтем 1-ю строку, умноженную на 3: 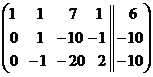 . К 3-ей строке прибавим 2-ю строку:
. К 3-ей строке прибавим 2-ю строку: 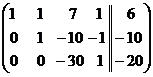 . Третью строку разделим на (-30):
. Третью строку разделим на (-30): 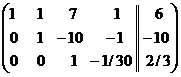 . Переменные
. Переменные 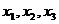 являются базисными, а переменная
являются базисными, а переменная 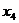 является свободной. Заменим исходную систему системой, полученной путём преобразования матрицы и выразим базисные переменные через свободные:
является свободной. Заменим исходную систему системой, полученной путём преобразования матрицы и выразим базисные переменные через свободные: 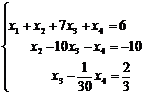 . Выразим из 3-го уравнения
. Выразим из 3-го уравнения 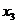 и подставим его значение во второе уравнение, затем из 2-го уравнения выразим
и подставим его значение во второе уравнение, затем из 2-го уравнения выразим 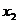 и подставим в 1-е уравнение. Тогда система примет вид:
и подставим в 1-е уравнение. Тогда система примет вид: 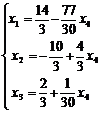 . Свободная переменная
. Свободная переменная 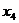 может принимать любые значения. Зададим
может принимать любые значения. Зададим 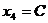 , где С- произвольная константа. Тогда решение системы может быть представлнно в виде матрицы-столбца:
, где С- произвольная константа. Тогда решение системы может быть представлнно в виде матрицы-столбца: 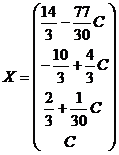 .
.
4) Даны векторы 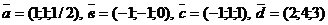 .
.
a)Доказать, что вектора 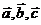 образуют базис и найти разложение вектора
образуют базис и найти разложение вектора 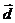 по этому базису.
по этому базису.
b) Найти скалярное произведение векторов 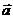 и
и 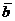 .
.
c) Найти векторное произведение векторов 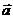 и
и 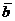 .
.
d) Найти смешанное произведение векторов 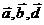 .
.
Решение:
a) Три вектора в трёхмерном пространстве образуют базис, если они линейно независимы. Для проверки линейной зависимости векторов составим их нулевую линейную комбинацию: 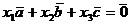 . Данное векторное уравнение соответствует системе трёх линейных однородных уравнений:
. Данное векторное уравнение соответствует системе трёх линейных однородных уравнений: 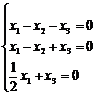 . Вычислим определитель матрицы, полученной системы:
. Вычислим определитель матрицы, полученной системы: 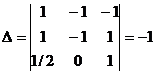 .
.
Т.к. определитель основной матрицы однородной системы 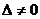 , то система имеет единственное нулевое решение
, то система имеет единственное нулевое решение 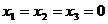 . Следовательно, по определению линейной зависимости векторов, векторы
. Следовательно, по определению линейной зависимости векторов, векторы 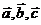 являются линейно независимыми , а значит образуют базис.
являются линейно независимыми , а значит образуют базис.
Найдём разложение вектора 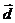 по этому базису. Составим линейную комбинацию:
по этому базису. Составим линейную комбинацию: 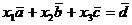 . Перепишем данное векторное уравнение в координатной форме:
. Перепишем данное векторное уравнение в координатной форме: 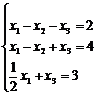 . Решая полученную систему (например, методом Крамера), найдём
. Решая полученную систему (например, методом Крамера), найдём 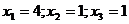 . Следовательно, разложение вектора
. Следовательно, разложение вектора 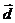 по базису
по базису 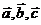 имеет вид:
имеет вид: 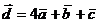 .
.
b) 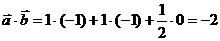 .
.
c) 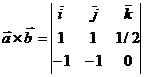 Раскрывая определитель по элементам 1-ой строки, получим:
Раскрывая определитель по элементам 1-ой строки, получим: 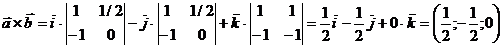 .
.
d) 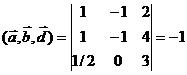 .
.
5) Даны координаты вершин треугольника, A(3, 5), B(-7, 12), C(2, -6). Найти:
a) длину стороны AB;
b) общие уравнения сторон AB и BC;
c) величину угла B;
d)длину и уравнение высоты, опущенной из вершины 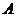 ;
;
e) площадь треугольника 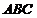 ;
;
f) уравнение прямой, проходящей через точку 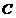 параллельно стороне
параллельно стороне 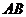 .
.
Решение:
a)Найдём длину стороны AB, как длину вектора 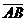 :
: 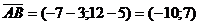 .
. 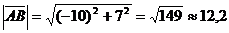 .
.
b)Найдём уравнения сторон AB и BCпо формуле уравнения прямой, проходящей через две точки.
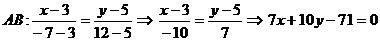 - общее уравнение прямой АВ.
- общее уравнение прямой АВ.
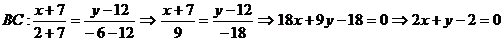 - общее уравнение прямой ВС.
- общее уравнение прямой ВС.
 c) Угол В – есть угол между прямыми AB и BC. Угол между прямыми может быть найден, как угол между их нормальными векторами.
c) Угол В – есть угол между прямыми AB и BC. Угол между прямыми может быть найден, как угол между их нормальными векторами. 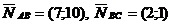 .
. 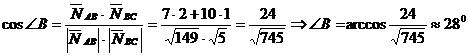 .
.
d) Опустим высоту из точки А на сторону ВС. Пусть точка D – есть основание этой высоты. Прямая AD перпендикулярна прямой ВС. Следовательно, вектор нормали прямой ВС является направляющим вектором для прямой AD. 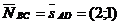 . Воспользуемся каноническим уравнением прямой.
. Воспользуемся каноническим уравнением прямой. 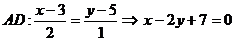 - общее уравнение высоты AD.
- общее уравнение высоты AD.
Найдём длину высоты AD, как расстояния от точки А до прямой ВС.
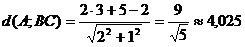 .
.
e)Найдём площадь треугольника 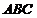 как половину произведения длины основания треугольника на его высоту.
как половину произведения длины основания треугольника на его высоту.
Пусть ВС – основание 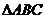 , AD – его высота.
, AD – его высота.
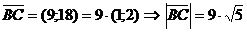 ;
; 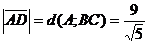 .
.
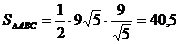 .
.
f) Обозначим прямую, проходящую через точку 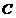 параллельно стороне
параллельно стороне 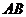 через l. Т.к.
через l. Т.к. 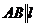 , то
, то 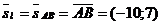 . Составим каноническое уравнение прямой l.
. Составим каноническое уравнение прямой l.
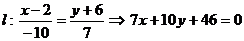 - общее уравнение прямой l.
- общее уравнение прямой l.
6) Даны четыре точки A(3;-2;1), B(1;2;4), C(-5;4;6), M(2;3;-1). Найти:
a)уравнение плоскости a, проходящей через три точки A, B, C;
b)каноническое уравнения прямой AB;
c)уравнение и длину высоты, опущенной из вершины М на грань 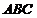 ;
;
d) объем пирамиды АВСМ.
Решение:
a)Воспользуемся уравнением плоскости, проходящей через три точки: 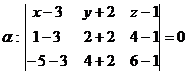
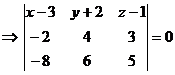
Разложим определитель по элементам первой строки:
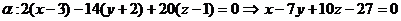 - общее уравнение плоскости α.
- общее уравнение плоскости α.
b) Воспользуемся уравнением прямой, проходящей через две точки:
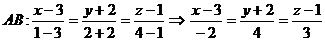 - каноническое уравнение прямой АВ.
- каноническое уравнение прямой АВ.
c) Обозначим высоту, опущенной из вершины М на грань 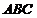 через l. Т.к
через l. Т.к 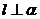 , то
, то 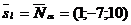 . Составим каноническое уравнение прямой l:
. Составим каноническое уравнение прямой l: 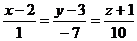 .
.
Найдём длину высоты как расстояние от точки М до плоскости α: 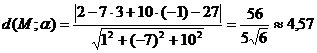 .
.
d)Объём пирамиды равен 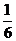 объёма параллелепипеда, построенного на трёх векторах и может быть вычислен через смешанное произведение этих векторов:
объёма параллелепипеда, построенного на трёх векторах и может быть вычислен через смешанное произведение этих векторов: 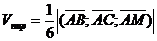 .
.
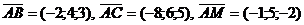
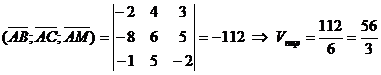 .
.
7) Дано уравнение кривой второго порядка 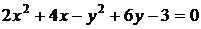 . Привести её к каноническому виду, определить вид, указать её параметры.
. Привести её к каноническому виду, определить вид, указать её параметры.
Решение:
Приведём данное уравнение к каноническому виду. Для этого выделим полные квадраты для переменных x и y:
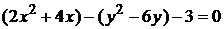 ,
,
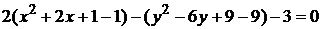 ,
,
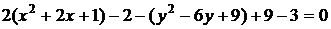 ,
,
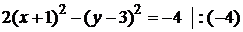 .
.
Таким образом, получили каноническое уравнение гиперболы со смещённым центром:
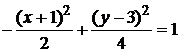 или
или 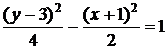 .
.
Точка 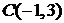 – центр гиперболы.
– центр гиперболы.
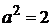

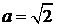 – мнимая полуось;
– мнимая полуось;
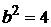

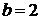 – действительная полуось;
– действительная полуось;
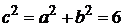

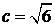 ;
;
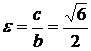 – эксцентриситет.
– эксцентриситет.
Точки 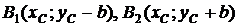 определяют вершины гиперболы:
определяют вершины гиперболы:
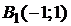 ,
, 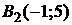 .
.
Точки 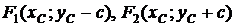 определяют фокусы гиперболы:
определяют фокусы гиперболы:
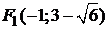 ,
, 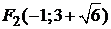 .
.
Уравнения 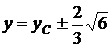 определяют директрисы гиперболы:
определяют директрисы гиперболы: 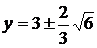 .
.
Уравнения 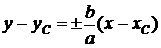 определяют асимптоты:
определяют асимптоты: 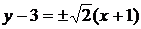 .
.
Начертим гиперболу 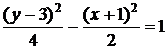 , используя найденные параметры (рис. 1).
, используя найденные параметры (рис. 1).
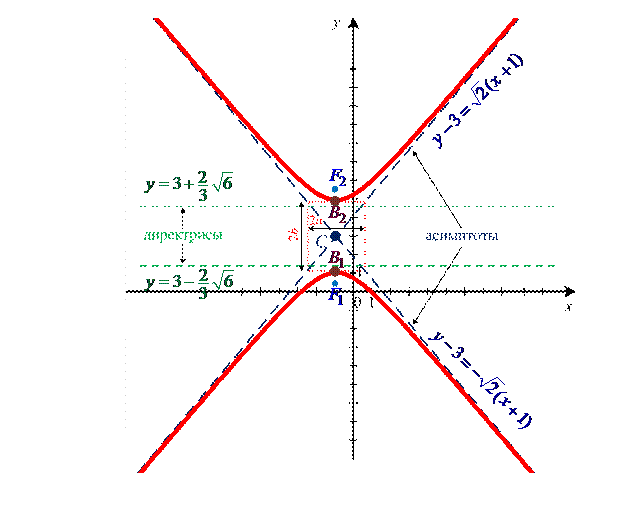
Рис. 1
Контрольная работа №2
1)Вычислить пределы, не пользуясь правилом Лопиталя.
Решение:
a) 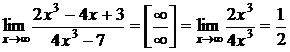 . Предел отношения многочленов и иррациональностей при
. Предел отношения многочленов и иррациональностей при 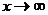 равен пределу отношения старших по степени слагаемых.
равен пределу отношения старших по степени слагаемых.
b) 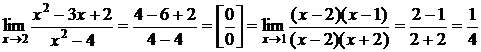 .
.
c) 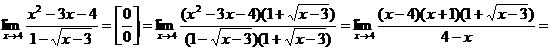
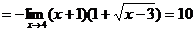 .
.
d) 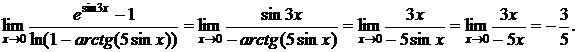
e)Воспользуемся обобщённой формулой второго замечательного предела:
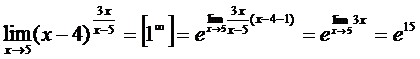 .
.
2) Исследовать функции на непрерывность. Классифицировать точки разрыва.
a) 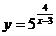 .
.
Решение:
Т.к. при 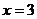 знаменатель дроби
знаменатель дроби 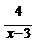 обращается в ноль, то
обращается в ноль, то 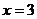 -есть точка разрыва данной функции. Найдём пределы при
-есть точка разрыва данной функции. Найдём пределы при 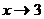 слева и справа.
слева и справа.
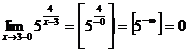 ,
, 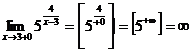 , следовательно
, следовательно 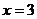 -есть точка разрыва второго рода.
-есть точка разрыва второго рода.
b) 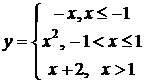
Решение:
Функции 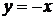 ,
, 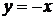 ,
, 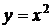 – элементарные и в области определения непрерывны. Точки разрыва возможны в переходных от одного задания к другому точках, т.е. в точках
– элементарные и в области определения непрерывны. Точки разрыва возможны в переходных от одного задания к другому точках, т.е. в точках 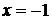 и
и 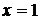 . Исследуем поведение функции в этих точках:
. Исследуем поведение функции в этих точках:
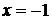 слева:
слева: 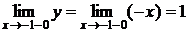 справа:
справа: 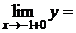
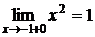 , тогда
, тогда 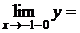
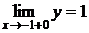 , т.е. функция непрерывна в точке
, т.е. функция непрерывна в точке 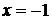
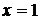 слева:
слева: 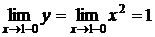 справа:
справа: 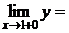
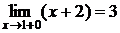 , тогда
, тогда 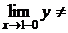
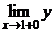 , т.е. функция имеет разрыв первого рода в точке
, т.е. функция имеет разрыв первого рода в точке 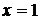 , т.к. пределы конечны.
, т.к. пределы конечны.
3) Найти производные первого порядка для следующих функций:
a) 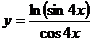
Решение:
Воспользуемся формулой для нахождения производной частного:
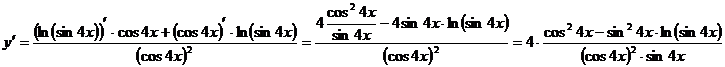 b)
b) 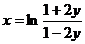
Решение:
Воспользуемся формулой для нахождения производной обратной функции:
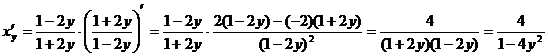
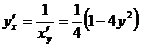
c) 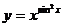
Решение:
Воспользуемся формулой логарифмического дифференцирования.
Найдём 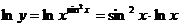
По формуле для нахождения производной от произведения:
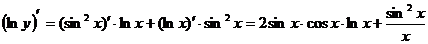 .
.
Следовательно 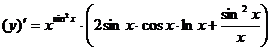 .
.
d) 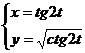
Решение:
Воспользуемся формулой для нахождения производной параметрически заданной функции: 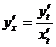 .
.
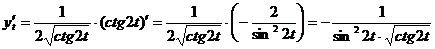
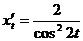 ;
;
Тогда 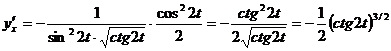 .
.
4) Найти уравнения касательной и нормали к графику функции 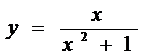
в точке x0=-2.
Решение:
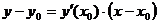 - уравнение касательной.
- уравнение касательной.
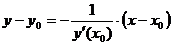 - уравнение нормали.
- уравнение нормали.
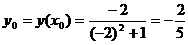 ;
;
По формуле для нахождения производной частного:
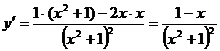 ;
; 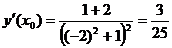 .
.
Тогда уравнение касательной: 
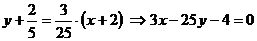 ;
;
Уравнение нормали: 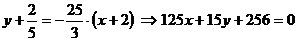 .
.
5) С помощью методов дифференциального исчисления построить график функции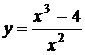 .
.
Решение:
1) Области определения функции не принадлежит только точка х=0:
D(y)=(-¥;0)È(0;+¥).
2) 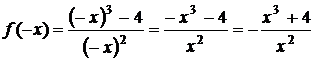
 функция общего вида (не чётная и не нечётная).
функция общего вида (не чётная и не нечётная).
Функция не периодична потому, что её область определения не имеет периодической структуры.
3)Найдём точки пересечения графика с осями координат.
С осью Ox: у=0, 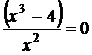

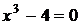 ,
, 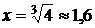
 точка
точка 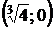 .
.
С осью Oy: при х=0 функция не существует  точек пересечения с осью Oy нет.
точек пересечения с осью Oy нет.
4)Найдем асимптоты функции.
Вертикальные:
Исследуем функцию в окрестности точки разрыва х=0.
Левосторонний предел 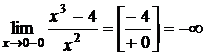 .
.
Правосторонний предел равен 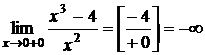

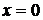 -двусторонняя вертикальная асимптота.
-двусторонняя вертикальная асимптота.
Наклонные и горизонтальные:
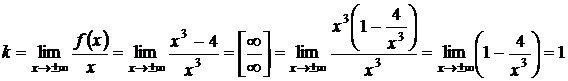
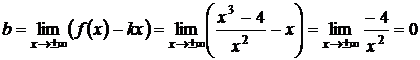

y=х – прямая, которая служит наклонной асимптотой графика как при x®-¥, так и при x®+¥.
5) Найдем критические точки: 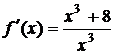

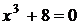
 х=-2.
х=-2.
Найдем интервалы монотонности (метод интервалов) и точки экстремума функции.
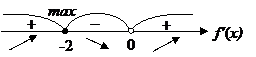
Интервалы монотонности: на интервале 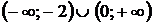 функция возрастает; на интервале
функция возрастает; на интервале 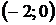 функция убывает.
функция убывает.
При х=-2- функция принимает максимальное значение 
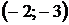 точка максимума.
точка максимума.
При х=0 – экстремума нет, так как в этой точке функция не определена.
6) Исследуем функцию на вогнутость, выпуклость и перегиб.
Найдём вторую производную 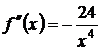 .
.
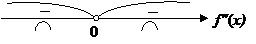
Интервалы выпуклости, вогнутости: на интервале 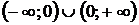 функция выпукла. Перегибов нет.
функция выпукла. Перегибов нет.
7) На рис.2 построена кривая, удовлетворяющая проведённому исследованию.
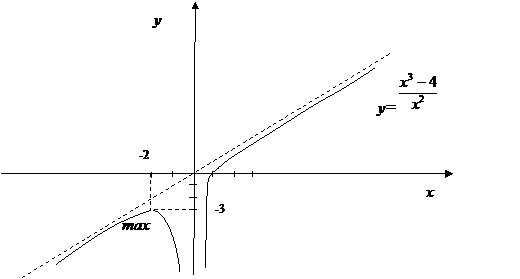
Рис. 2
6)Найти наибольшее и наименьшее значения функции 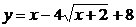
на отрезке 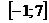 .
.
Решение:
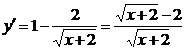 . Найдём критические точки:
. Найдём критические точки:
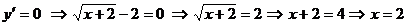
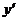 не существует, если
не существует, если 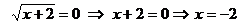
Точка 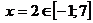 ,
, 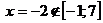 .
.
Найдём 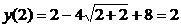 .
.
Найдём значения функции на концах отрезка:
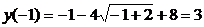 ;
; 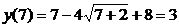 .
.
Наибольшее значение на данном отрезке достигается функцией в двух точках – на концах отрезка: 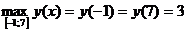 .
.
Наименьшее значение на данном отрезке достигается функцией во внутренней точке отрезка: 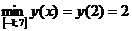 .
.
7)Даны функция 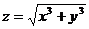 и точки A(1; 2), B(1,02; 1,97).
и точки A(1; 2), B(1,02; 1,97).
Вычислить
a) значение функции 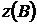 ;
;
b) 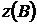 с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
c) Составить уравнения касательной плоскости и нормали к поверхности ,заданной данной функцией в точке C (x0, y0, z0).
Решение:
a) 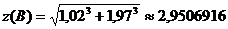 .
.
b) Воспользуемся формулой: 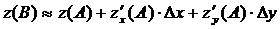 .
.
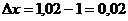 ;
; 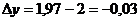 ;
; 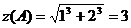 .
.
Найдем 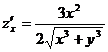 ,
, 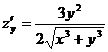 , тогда
, тогда 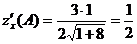 ,
, 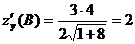 .
.
Следовательно, получим: 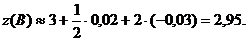
Оценим относительную погрешность вычисления: 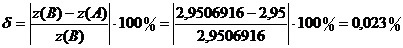 .
.
c) C (1; 2; 3)
Составим уравнение касательной плоскости : 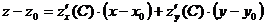
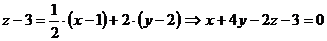
Составим уравнение нормали: 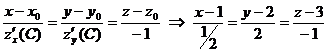 .
.
8) Даны функция 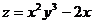 , точка A(2;-1) и вектор
, точка A(2;-1) и вектор 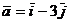 . Требуется найти
. Требуется найти 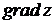 и производную в точке A по направлению вектора
и производную в точке A по направлению вектора 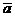 .
.
Решение:
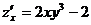 ;
; 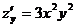 ;
; 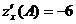 ;
; 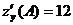
Следовательно 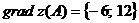 .
.
Найдём направляющие косинусы вектора 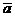 :
:
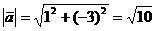 ;
; 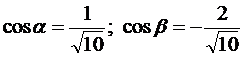 .
.
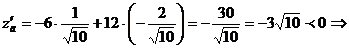 данная функция убывает в направлении вектора
данная функция убывает в направлении вектора 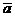
9) Найти экстремум функции 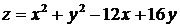 и ее наибольшее и наименьшее значения в области
и ее наибольшее и наименьшее значения в области 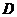 :
: 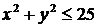 .
.
Решение:
Найдем стационарные точки функции из системы: 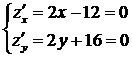 .
.
М(6; -8)- стационарная точка. 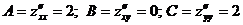 .
.
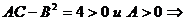 точка М0(6; -8) является точкой минимума функции.
точка М0(6; -8) является точкой минимума функции.
Стационарная точка М0 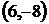 не лежит в заданном круге. Поэтому наибольшее и наименьшее значения функция принимает на границе области, т.е. на окружности
не лежит в заданном круге. Поэтому наибольшее и наименьшее значения функция принимает на границе области, т.е. на окружности 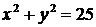 .
.
Составим функцию Лагранжа 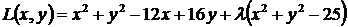 .
.
Ее стационарные точки найдем из системы 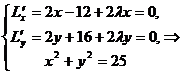
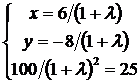 , откуда
, откуда 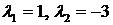 . Следовательно, стационарными точками границы являются М1(3, -4) и М2(-3, 4).
. Следовательно, стационарными точками границы являются М1(3, -4) и М2(-3, 4). 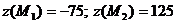 . Эти числа являются наименьшим и наибольшим значениями z в заданной области:
. Эти числа являются наименьшим и наибольшим значениями z в заданной области: 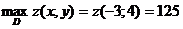 ;
; 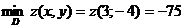 .
.
Список рекомендуемой литературы.
1. Агишева Д. К. Матрицы и их приложение к решению систем линейных уравнений: Учебное пособие/ Д. К. Агишева, С. А. Зотова, В. Б. Светличная. - Волгоград, РПК «Политехник», 2001. – 63с.
2. Александрова Л. А, Александрова В. А, Зотова С. А., Светличная В. Б., Матвеева Т. А., Короткова Н. Н. Математика. I часть: Учебное пособие (для студентов заочной формы обучения) / – Волгоград, РПК «Политехник», 2003. – 84с.
3. Письменный Д. Т. Конспект лекций по высшей математике. 1 часть. – М.: Рольф, 2000. – 288 с., с илл.
4. Данко П. Е.,Попов А. Г.,Коевникова Т. Я. Высшая математика в упранениях и задачах. Том 1 – М.: Высшая школа, 1980 – 320 с., с илл.
5. Зотова С. А., Светличная В. Б., Матвеева Т. А.. Практическое руководство по аналитической геометрии: Учебное пособие / – Волгоград, РПК «Политехник», 2003. – 41с.
6. Клетеник Д. В. Сборник задач по аналитической геометрии: Учебное пособие для втузов – СПб: «Специальная Литература», 1998.–200 с.: илл.
7. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1981.–720с.: илл.
8. Выгодский М. Я. Справочник по высшей математике. –М.: Гостехтеоргиздат, 1973.
Вопросы к экзамену по математике.
