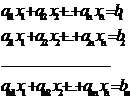Обратная матрица. Определение, существование, вычисление.

Для любой квадратной невырожденной матрицы А порядка n (detA 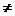0) существует обратная матрица А^-1 такая, что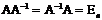

Обратная матрица может быть найдена по формуле :

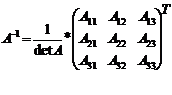
где 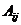- алгебраическое дополнение элемента 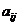матрицы А.

Свойства обратной матрицы:

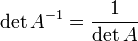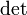, где обозначает определитель.

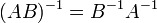для любых двух обратимых матриц A и B.

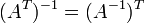где * ^T обозначает транспонированную матрицу.

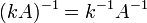для любого коэффициента .

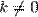Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерностьпространства

решений больше нуля, либо их нет вовсе.

Ранг матрицы

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля, и называется вырожденной, если D = 0.

Говорят, что ненулевая матрица А имеет ранг rang(A)=S, если А имеет по меньшей мере одну невырожденную подматрицу порядка S, а все подматрицы А более высоких порядков вырождены.

Нахождение ранга матрицы данным образом (т.е. по определению) является достаточно трудоемким процессом. Поэтому на практике ранг матрицы вычисляют иначе, используя следующую теорему.

Теорема. Ранг матрицы не изменяется:

1) при перестановке двух строк матрицы;

2) при умножении какой-либо строки на число С 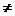0;

3) при сложении любого кратного одной строки с другой строкой;

4) при транспонировании А.

Теоремы, указанные выше для строк, справедливы и для столбцов.

Нахождение ранга матрицы А сводится к тому, чтобы с помощью данной теоремы матрицу А перевести в трапециевидную матрицу 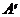равного ранга:

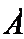
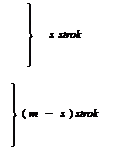
s столбцов ( n- s ) столбцов

в которой :

1) все элементы, стоящие ниже главной диагонали, равны нулю;

2) или все элементы последних( m - s) строк обращаются в нуль, или m= s

3) все элементы начала главной диагонали 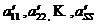отличны от нуля.

Тогда rang (A)= rang ( 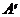) = s (число главных диагональных элементов, отличных от нуля). Преобразование матрицы А в трапециевидную матрицу 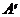равного ранга проводится методом, который называется алгоритмом Гаусса: 1) Так как не все элементы А равны нулю, то перестановкой строк и столбцов можно добиться того, чтобы первый главный диагональный элемент был отличен от нуля .

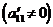2) Сложением первой строки, умноженной на соответствующий множитель, с другими строками всегда можно добиться, чтобы все элементы, стоящие ниже 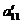, были равны нулю.

3) Если в строках со 2-й по последнюю имеется по крайней мере один ненулевой элемент, то он с помощью перестановок строк и столбцов может быть поставлен на второе место в главной диагонали. Тогда, складывая теперь уже вторую строку, умноженную на соответствующий множитель с нижними строками, получаем, что все элементы второго столбца. стоящие ниже второго главного диагонального элемента, равны нулю, и т.д., пока не получим трапециевидную матрицу.

Пример :

А= ~ ~ ~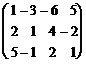

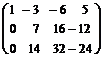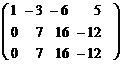( ко 2-й строке прибавили ( разделили 3-ю строку на 2) 1-ю, умноженную на (-2); к 3-й строке прибавили 1-ю, умноженную на (-5)

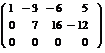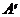~ = ; rang (A) = rang ( 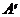) = 2

( из 3-й строки вычли 2-ю).

Теорема о ранге матрицы.

Ранг матрицы равен максимальному числу линейно независимых строк (столбцов).

Строки А_{1 ,} А_{2 , .........} А_К называются линейно независимыми, если их линейная комбинация равна нулю. 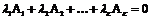только при нулевых значениях коэффициентов .

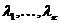5. Матричная форма записи системы линейных алгебраических уравнений. Виды СЛАУ:

Система уравнений вида.

(1)

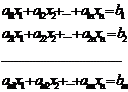
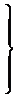
Называется системой m линейных уравнений с n неизвестными .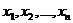

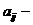коэффициенты при неизвестных, 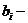свободные члены.

Если все свободные члены равны нулю, то система называется однородной.

Решением системы линейных уравнений (1) называется такая система n чисел 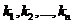, что каждое из уравнений системы (1) превращается в тождество после замены в нем неизвестных 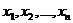соответствующими числами .

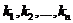Совокупность всех решений называется множеством решений.

Две системы линейных уравнений называются эквивалентными, если они имеют одинаковые множества решений.

Если система линейных уравнений не имеет ни одного решения, то она называется несовместной, например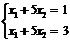

Cовместная система называется определенной, если она имеет единственное решение: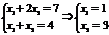

Совместная система называется неопределенной, если решений больше, чем одно: 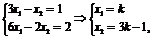где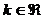

Теория системы линейных уравнений может быть наглядно описана с помощью матриц. Коэффициенты при неизвестных в системе (1) записывают в виде матрицы размера (m 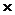n) :

А = 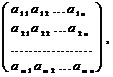которая называется матрицей системы (1).

Свободные члены образуют столбец размера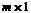

В = 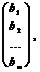который называется столбцом свободных членов.

Неизвестные записываются тоже в виде столбца размера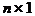

X = .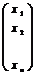

Тогда систему (1) можно записать в виде

(2) АХ = В

Такая запись называется матричной записью системы.

Убедимся, что это действительно так:

АХ = =

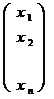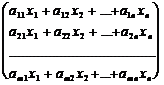
Мы получили левую часть системы (1).

Далее, из равенства матриц АХ и В следует, что соответствующие их элементы равны, и мы получаем следующую систему равенств: