Вычисление определителей 1-го, 2-го и 3-го порядков.
1) Если матрица состоит из одного элемента, то определитель матрицы равен значению этого элемента: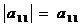 
2) Если матрица второго порядка, то ее определитель равен разности между произведением элементов, стоящих на главной диагонали, и произведением элементов, стоящих на побочной диагонали: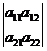 
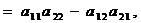
т.е. вычисляется по правилу “ произведение главных диагональных элементов минус произведение побочных диагональных элементов “.
3) Определитель 3-го порядка равен сумме 6 слагаемых, три из которых берутся со знаком “ + “, а оставшиеся три - со знаком “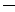 
“:
= 
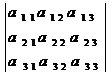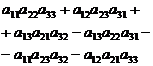Для того, чтобы облегчить запоминание этой громоздкой формулы, пользуются так называемым правилом треугольников Oпределители более высоких порядков в принципе тоже можно было бы вычислить по определению. однако это требует очень больших усилий.
Поэтому поступают следующим образом: определитель n -го порядка сводят к определителям ( n-1)-го порядка и т.д., до тех пор, пока не получат определители 3-го или 2-го порядка. В основе этого принципа “ постепенного понижения порядка “ лежит теорема разложения.
Теорема разложения.
Определитель n -го порядка равен сумме произведений всех элементов какой-либо строки ( или столбца ) на соответствующие алгебраические дополнения: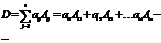 
-“ разложение по элементам i -ой строки “или
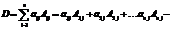
-“ разложение по элементам j -го столбца “
Алгебраическое дополнение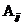 
элемента 
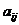есть. минор 
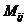, домноженный на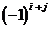 
Минором 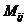элемента 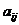называют определитель порядка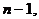 
получающийся из D вычеркиванием i-ой строки и j-го столбца .
Т.о., следуя теореме разложения, определитель n -го порядка D записывается в виде суммы n определителей порядка ( n-1 );
к каждому из этих определителей порядка n - 1 вновь может быть применена теорема разложения.
Вычисления определителей существенно упрощаются, если перед разложением определителя по элементам i -й строки ( j - го столбца) как можно больше из них будут превращены в нули. Это становится возможным благодаря применению свойств определителей.
Свойства определителей.
1.Определитель не изменит своего значения, если поменять в нем местами строки и столбцы, т.е. транспонировать определитель
det A = det AT
Поэтому все свойства, сформулированные ниже для строк, верны и для столбцов.
2.Перестановка двух строк меняет знак определителя на противоположный.
3.Общий для всех элементов строки множитель можно выносить за знак определителя.
4.При сложении двух определителей, отличающихся только одной строкой, соответствующие элементы этой строки складываются, остальные остаются без изменения.
5.Прибавление к элементам i-ой строки соответствующих элементов К-ой строки, умноженных на какое-либо число, не изменяет значение определителя.
6.Определитель равен нулю, если одна строка целиком состоит из нулей или если две строки равны или пропорциональны друг другу.