Уравнений кривых второго порядка
■ Преобразование координат. Задача преобразования координат на плоскости состоит в том, чтобы, зная координаты любой точки плоскости М(х, у), найти координаты 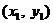 этой же точки в другой системе координат. Формулы, связывающие координаты точки М в "старой" и "новой" системах координат, называются формулами преобразования координат. При удачном выборе новой системы координат можно добиться, чтобы уравнение линии приняло наиболее простой канонический вид (что позволит исследовать свойства линии и облегчит ее построение).
этой же точки в другой системе координат. Формулы, связывающие координаты точки М в "старой" и "новой" системах координат, называются формулами преобразования координат. При удачном выборе новой системы координат можно добиться, чтобы уравнение линии приняло наиболее простой канонический вид (что позволит исследовать свойства линии и облегчит ее построение).
1-й случай. Пусть требуется перейти от системы координат хОу к новой системе координат 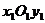 , начало которой находится в точке
, начало которой находится в точке 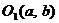 (где а и b – координаты точки
(где а и b – координаты точки 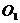 в старой системе координат), а новые оси
в старой системе координат), а новые оси 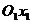 и
и 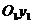 параллельны старым осям Ох и Оу (и одинаково с ними направлены). Тогда между координатами произвольной точки в этих двух системах координат имеется следующая зависимость:
параллельны старым осям Ох и Оу (и одинаково с ними направлены). Тогда между координатами произвольной точки в этих двух системах координат имеется следующая зависимость:
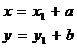 (1)
(1)
Эти формулы позволяют выразить первоначальные координаты точки x, y через ее новые координаты и координаты нового начала в старой системе координат.
Если же требуются формулы обратного перехода, выражающие новые координаты через старые, то из (1) легко видеть, что
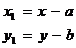 (2)
(2)
Пример 1. Даны координаты точки 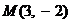 в системе хОу. Перенесем начало координат в точку
в системе хОу. Перенесем начало координат в точку 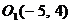 , сохраняя направления осей. Найти новые координаты точки М.
, сохраняя направления осей. Найти новые координаты точки М.
Решение. Имеем 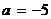 ,
, 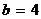 ; тогда по формулам (2)
; тогда по формулам (2) 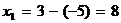 ,
, 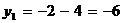 .
.
Ответ: 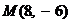 .
.
Пример 2. С помощью параллельного переноса осей координат (без изменения их направления) упростить уравнение линии 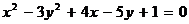 .
.
Решение. Выделим в левой части уравнения полные квадраты:
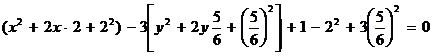
или 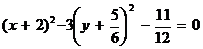 ,
,
откуда 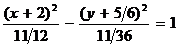 .
.
Воспользуемся формулами (2): 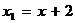
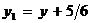 .
.
Отсюда видно, что если взять 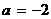 ,
, 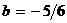 , т.е. перенести начало координат в точку
, т.е. перенести начало координат в точку 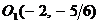 , то в новой системе координат
, то в новой системе координат 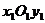 уравнение примет вид
уравнение примет вид 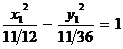 , откуда видно, что исходное уравнение определяет гиперболу, действительная полуось которой
, откуда видно, что исходное уравнение определяет гиперболу, действительная полуось которой 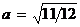 , мнимая полуось
, мнимая полуось 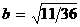 , а центр находится в точке
, а центр находится в точке 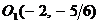 .
.
2-й случай. Пусть требуется перейти от системы координат хОу к новой системе координат 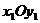 (с тем же самым началом О), которая получается при повороте осей координат на угол
(с тем же самым началом О), которая получается при повороте осей координат на угол 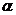 (рис. 6). Тогда имеют место соотношения
(рис. 6). Тогда имеют место соотношения
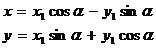
 . (3)
. (3)
Формулы обратного перехода имеют вид
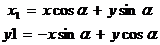 . (4)
. (4)
Пример 3. Дана точка 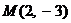 . Найти ее координаты в системе координат
. Найти ее координаты в системе координат 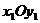 , повернутой на угол 30° против часовой стрелки относительно исходной системы (без изменения начала координат).
, повернутой на угол 30° против часовой стрелки относительно исходной системы (без изменения начала координат).
Решение. Имеем 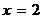 ,
, 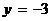 ,
, 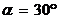 . Тогда по формулам (4)
. Тогда по формулам (4)
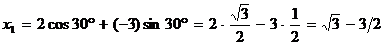 ,
,
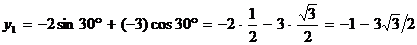 .
.
Ответ: 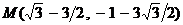 .
.
Замечание. Можно объединить соотношения (1) и (3), получая формулы преобразования координат при параллельном переносе и повороте системы координат:
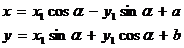 .
.
Тогда формулы обратного перехода будут иметь вид
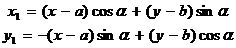 .
.
■ Упрощение уравнений кривых второго порядка. Общее уравнение второй степени имеет вид
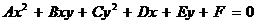 (5)
(5)
(где коэффициенты А, В, С не равны нулю одновременно).
Рассмотренные выше окружность, эллипс, гипербола и парабола имеют уравнения, которые являются частными случаями общего уравнения (5) (поэтому их называют кривыми второго порядка). Однако этому уравнению могут соответствовать и другие геометрические образы, иллюстрируемые следующими примерами.
Пример 4. Уравнение 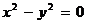 определяет пару пересекающихся прямых, т.к. его можно записать в виде
определяет пару пересекающихся прямых, т.к. его можно записать в виде 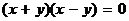 , откуда получаем
, откуда получаем 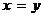 и
и 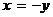 .
.
Пример 5. Уравнению 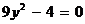 отвечает пара параллельных прямых
отвечает пара параллельных прямых 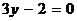 и
и 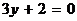 .
.
Пример 6. Уравнению 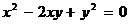 , которое можно переписать в виде
, которое можно переписать в виде 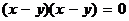 , отвечает одна прямая
, отвечает одна прямая 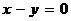 (или, как еще говорят, пара слившихся прямых).
(или, как еще говорят, пара слившихся прямых).
Пример 7. Уравнению 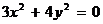 удовлетворяют только значения
удовлетворяют только значения 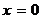 ,
, 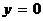 , т.е. оно определяет одну точку
, т.е. оно определяет одну точку 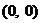 ("вырожденный эллипс").
("вырожденный эллипс").
Пример 8.Уравнению 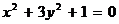 не удовлетворяют никакие значения х и у, так что оно не определяет никакого геометрического образа ("мнимый эллипс").
не удовлетворяют никакие значения х и у, так что оно не определяет никакого геометрического образа ("мнимый эллипс").
Можно доказать, что все возможные случаи, которые могут встретиться при исследовании общего уравнения второй степени (5), исчерпываются либо кривыми второго порядка; либо ситуациями в Примерах 4 – 8.
Составим из коэффициентов уравнения два определителя:
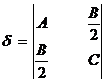 и
и 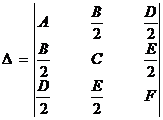 .
.
В зависимости от значений этих определителей уравнение (5) определяет следующий геометрический образ (см. таблицу):
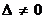 | 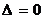 | |
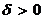 | Эллипс (или нет геометрического образа) | Точка |
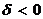 | Гипербола | Пара пересекающихся прямых |
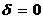 | Парабола | Пара параллельных прямых или одна прямая |
Задача упрощения уравнения (5) состоит в том, чтобы при переходе к новой системе координат добиться устранения члена с произведением координат. Практически такой переход можно осуществить следующим образом.
1-й случай. Если 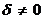 , то геометрический образ имеет центр симметрии
, то геометрический образ имеет центр симметрии 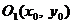 . Координаты центра находятся из системы уравнений
. Координаты центра находятся из системы уравнений
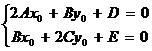 . (6)
. (6)
После переноса начала координат в новый центр уравнение (5) в системе координат 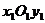 примет вид
примет вид
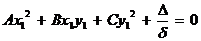 . (7)
. (7)
Далее повернем систему координат 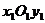 на угол
на угол 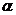 , определяемый формулой
, определяемый формулой 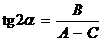 (если
(если 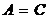 , то угол поворота 45°). При этом координаты
, то угол поворота 45°). При этом координаты 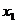 ,
, 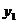 заменяются на новые координаты
заменяются на новые координаты 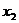 ,
, 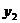 по формулам поворота:
по формулам поворота:
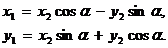 (8)
(8)
Теперь последнее уравнение примет канонический вид
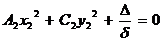 ,
,
из которого легко распознать вид геометрического образа и расположение на плоскости.
2-й случай. Если 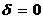 , то отвечающий уравнению (5) геометрический образ не имеет определенного центра симметрии. При этом система уравнений (6) либо совсем не имеет решений, либо имеет бесконечно много решений. Тогда рекомендуется действовать иначе, чем в случае, когда
, то отвечающий уравнению (5) геометрический образ не имеет определенного центра симметрии. При этом система уравнений (6) либо совсем не имеет решений, либо имеет бесконечно много решений. Тогда рекомендуется действовать иначе, чем в случае, когда 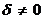 .
.
Если повернуть оси координат на угол 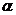 , определяемый как в предыдущем случае, старые координаты х, у выразятся через новые координаты
, определяемый как в предыдущем случае, старые координаты х, у выразятся через новые координаты 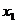 ,
, 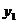 по формулам (3), произведение координат исчезнет, а уравнение (5) примет вид:
по формулам (3), произведение координат исчезнет, а уравнение (5) примет вид:
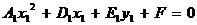 , или
, или
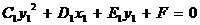 .
.
Остается выделить полный квадрат, вид геометрического образа и его расположение на плоскости.
Замечание. В подробных курсах аналитической геометрии приводится ряд других приемов процедуры приведения общего уравнения кривой второго порядка к каноническому виду.
Пример 9. Выяснить, какую линию определяет уравнение 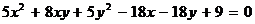 и привести его к каноническому виду.
и привести его к каноническому виду.
Решение. 1) Составим определители 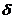 и
и 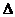 (см. стр. ___):
(см. стр. ___):
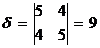 ,
, 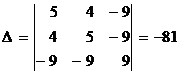 .
.
Так как 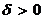 ,
, 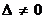 , то данная линия является эллипсом (см. таблицу на стр. ___).
, то данная линия является эллипсом (см. таблицу на стр. ___).
2) Составим систему уравнений для нахождения координат центра эллипса 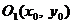 :
:
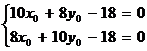 ,
,
откуда 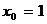 ,
, 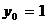 .
.
3) Перенесем начало координат в центр 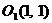 (без поворота осей). Тогда в системе координат
(без поворота осей). Тогда в системе координат 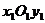 уравнение кривой примет вид (7):
уравнение кривой примет вид (7):
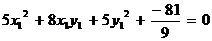 .
.
4) Теперь повернем систему координат 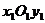 на угол
на угол 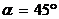 (против часовой стрелки), так как здесь
(против часовой стрелки), так как здесь 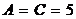 . При этом новые координаты
. При этом новые координаты 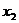 ,
, 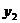 связаны с координатами
связаны с координатами 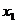 ,
, 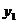 соотношениями (8):
соотношениями (8):
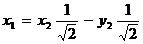 ,
,
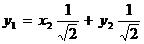 .
.
Если преобразовать по этим формулам последнее уравнение, то, согласно общей теории, член с произведением координат исчезнет и мы получим 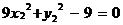 или
или 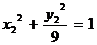 – каноническое уравнение эллипса с полуосями
– каноническое уравнение эллипса с полуосями 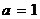 ,
, 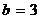 , фокусы которог
, фокусы которог
 |
о расположены на оси
 (см. рис. 7).
(см. рис. 7).Примеры уравнений кривых в полярных координатах
Уравнения некоторых кривых в полярных координатах выглядят значительно проще, чем в декартовой системе координат. Приведем примеры (для простоты на всех рисунках предполагается, что параметр а положителен).
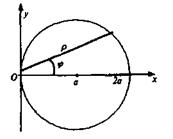 Окружность Окружность 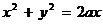 или или 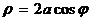 Рис. 8 Рис. 8 | 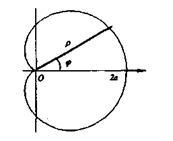 Кардиоида Кардиоида 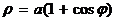 Рис. 9 Рис. 9 |
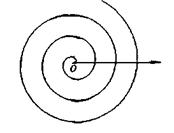 Спираль Архимеда Спираль Архимеда 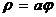 Рис. 10 Рис. 10 | 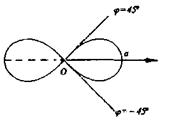 Лемниската Бернулли Лемниската Бернулли 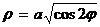 Рис. 11 Рис. 11 |
