Упрощение уравнения линии второго порядка
Определение 35. Линией второго порядка называется множество точек плоскости, которое в некоторой АСК можно задать уравнением второй степени от двух переменных.
Примерами таких линий являются окружность, эллипс, гипербола и парабола. Очевидно, в различных системах координат одна и та же линия будет задаваться различными уравнениями. При изучении этих линий прежде всего встают вопросы:
· Как выбрать такую систему координат, в которой линия имела бы наиболее простое уравнение.
· Какие существуют типы линий второго порядка.
Для решения этих вопросов нужно знать, как преобразуются координаты точек при переходе от одной системы координат к другой.
4.2.1. Преобразование аффинных координат на плоскости
Пусть на плоскости заданы две системы аффинных координат реперами R = 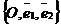 и R1 =
и R1 = 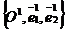 , где О1(х0, у0)R,
, где О1(х0, у0)R, 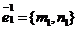 ,
, 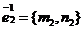 . Пусть М – произвольная точка плоскости, М(х, у)R и М(х1, у1
. Пусть М – произвольная точка плоскости, М(х, у)R и М(х1, у1 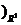 . Поставим задачу: найти связь между координатами х, у и х1, у1.
. Поставим задачу: найти связь между координатами х, у и х1, у1.
М(х, у)R Þ 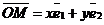 ; М(х1, у1 ; М(х1, у1 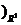 Þ Þ 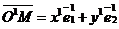 ; О1(х0, у0)R Þ ; О1(х0, у0)R Þ 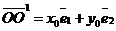 ; ; 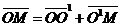 . Отсюда следует, что . Отсюда следует, что 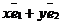 = = 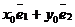 + + 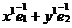 . Так как . Так как 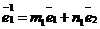 и и 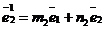 , то получаем , то получаем 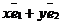 = ( = ( 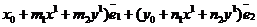 . . | 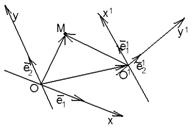 Рис. 76 Рис. 76 |
В левой и правой частях полученного равенства стоят разложения векторов по базису 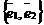 . Так как равные векторы имеют равные координаты, то
. Так как равные векторы имеют равные координаты, то
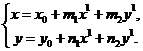 (63)
(63)
Так как 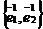 - базис, то
- базис, то 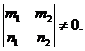
Очевидно и обратное. Если заданы формулы (63) с отличным от нуля определителем, то их можно рассматривать, как формулы, связывающие координаты одной и той же точки, если первая система аффинных координат задана произвольным репером R = 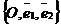 , а вторая система координат задана репером R1 =
, а вторая система координат задана репером R1 = 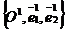 , где О1(х0, у0)R,
, где О1(х0, у0)R, 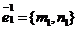 ,
, 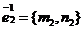 .
.
Замечание. Часто первую систему координат называют «старой» системой координат, а координаты точки в этой системе координат – «старыми» координатами. При этом вторую систему координат называют «новой».
Формулы (63) называются формулами преобразования аффинных координат. В этих формулах старые координаты точки выражаются через новые координаты этой же точки.
Если системы аффинных координат отличаются только началом координат, т.е. R1 = 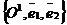 , то формулы преобразования координат будут иметь вид х1= х + х0 , у1= у + у0. Если обе системы координат имеют общее начало координат, то в формулах (63) не будет свободных членов.
, то формулы преобразования координат будут иметь вид х1= х + х0 , у1= у + у0. Если обе системы координат имеют общее начало координат, то в формулах (63) не будет свободных членов.
4.2.2. Преобразование прямоугольных координат
Пусть на плоскости даны две системы прямоугольных координат, заданные реперами R = 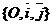 и R1=
и R1= 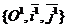 , О1(х0, у0)R и
, О1(х0, у0)R и 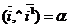 (рис. 61). Пусть М(х, у)R и М(х1, у1
(рис. 61). Пусть М(х, у)R и М(х1, у1 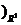 .
.
Так как прямоугольная система координат является частным случаем аффинной, то можно воспользоваться формулами (63), но для этого нужно найти старые координаты векторов 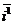 и и 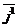 . Возможны два случая: 1) Реперы R = . Возможны два случая: 1) Реперы R = 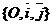 и R1= и R1= 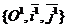 одинаково ориентированы. Так как одинаково ориентированы. Так как 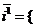 пр пр 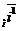 , пр , пр 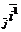 ) = (cosa, sina) ) = (cosa, sina) | 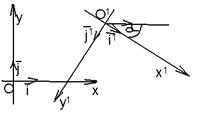 Рис. 77 Рис. 77 |
и 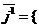 пр
пр 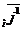 , пр
, пр 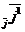 ) = (-sina, cosa), то формулы (9) будут иметь вид
) = (-sina, cosa), то формулы (9) будут иметь вид
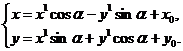 (64)
(64)
2) Реперы R = 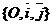 и R1=
и R1= 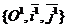 противоположно ориентированы.
противоположно ориентированы.
В этом случае формулы (9) примут вид 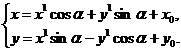 (65)
(65)
4.2.3. Преобразование уравнения линии второго порядка при повороте системы координат
Общий вид уравнения линии Г второго порядка в любой системе аффинных координат:
Г: а11х2 +2а12ху + а22у2 + 2а13х + 2а23у + а33 = 0 (66)
Если в уравнении (66) коэффициент а12 = 0, то уравнение (66) упрощается выделением полных квадратов (мы это сделаем ниже). Пусть а12 ¹ 0. Поставим вопрос, можно ли найти такую систему координат, чтобы в уравнении линии Г не было слагаемого с произведением координат. Пусть линия Г задана в прямоугольной системе координат. Решить поставленный вопрос попробуем с помощью поворота прямоугольной системы координат. В этом случае формулы преобразования координат:
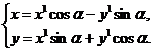 (67)
(67)
Подставив в уравнение (66), получим
а11(х1соsa - у1sina)2 + 2а12(х1соsa - у1sina)(х1 sina + у1 соsa) + а22(х1 sina + у1 соsa)2 + + 2а13(х1соsa - у1sina) + 2а23(х1 sina + у1 соsa) + а33 = 0.
Раскроем скобки, приведём подобные и запишем уравнение в виде
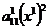 + 2
+ 2 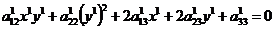 (68)
(68)
Новые коэффициенты выражаются через старые по формулам:
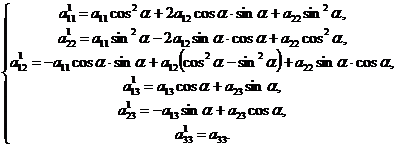 (69)
(69)
