Исследование взаимного расположения двух плоскостей
Дано: R = 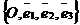 , П1 : А1х + В1у + С1z + D1 = 0, П2 : А2х + В2у + С2z + D2 = 0.
, П1 : А1х + В1у + С1z + D1 = 0, П2 : А2х + В2у + С2z + D2 = 0.
Исследовать взаимное расположение П1, П2 .
Решение. Задача сводится к исследованию системы  (46)
(46)
Возможны случаи.
1. А1, В1, С1 и А2, В2, С2 не пропорциональны. В этом случае система (46) имеет бесконечно много решений, но уравнения не пропорциональны. На геометрическом языке получаем, что плоскости имеют бесконечно много общих точек, но не совпадают. Следовательно, П1 и П2 пересекаются по прямой.
Замечание. Если прямая задана общими уравнениями (19), то каждое отдельно взятое уравнение задаёт прямую, т.е. прямая задаётся как линия пересечения двух плоскостей.
2.  . В этом случае уравнения системы (46) эквивалентны, т.е. каждое решение одного из них является решением второго. На геометрическом языке: каждая точка одной плоскости лежит на другой, т.е. плоскости совпадают.
. В этом случае уравнения системы (46) эквивалентны, т.е. каждое решение одного из них является решением второго. На геометрическом языке: каждая точка одной плоскости лежит на другой, т.е. плоскости совпадают.
3.  . В этом случае системы (46) не имеет решений. На геометрическом языке: плоскости не имеют общих точек.
. В этом случае системы (46) не имеет решений. На геометрическом языке: плоскости не имеют общих точек.
Следствие. Плоскости П1 : А1х + В1у + С1z + D1 = 0, П2 : А2х + В2у + С2z + D2 = 0 параллельны тогда и только тогда, когда  .
.
Задача 16. Исследовать взаимное расположение плоскостей, если одна из них задании общим уравнением, а вторая – параметрическими уравнениями.
Дано: R = 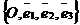 , П1 : Ах + Ву + Сz + D = 0, П2 :
, П1 : Ах + Ву + Сz + D = 0, П2 :  Исследовать взаимное расположение П1, П2 .
Исследовать взаимное расположение П1, П2 .
Решение. Задача сводится к исследованию системы  (*)
(*)
Подставив выражения х, у, z в первое уравнение и преобразовав его, получим
 (**)
(**)
Возможны случаи:
1)  ¹ 0 ( или
¹ 0 ( или  ¹ 0). В этом случае уравнение (**) имеет бесконечно много решений, зависящих от одного параметра. Следовательно, система (*) тоже имеет бесконечно много решений, зависящих от одного параметра. На геометрическом языке это значит, что плоскости пересекаются по прямой.
¹ 0). В этом случае уравнение (**) имеет бесконечно много решений, зависящих от одного параметра. Следовательно, система (*) тоже имеет бесконечно много решений, зависящих от одного параметра. На геометрическом языке это значит, что плоскости пересекаются по прямой.
2)  = 0,
= 0,  = 0,
= 0,  = 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + 0 = 0. Этому уравнению удовлетворяют все возможные значения u и v. На геометрическом языке это значит, что все точки первой плоскости лежат на второй и наоборот. Следовательно, плоскости совпадают.
= 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + 0 = 0. Этому уравнению удовлетворяют все возможные значения u и v. На геометрическом языке это значит, что все точки первой плоскости лежат на второй и наоборот. Следовательно, плоскости совпадают.
3)  = 0,
= 0,  = 0,
= 0,  ¹ 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + (
¹ 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + (  ) = 0. Это уравнение не имеет ни одного решения. На геометрическом языке это значит, что данные плоскости не имеют общих точек.
) = 0. Это уравнение не имеет ни одного решения. На геометрическом языке это значит, что данные плоскости не имеют общих точек.
Следствие. Если П1 : Ах + Ву + Сz + D = 0, П2 :  то П1 || П2 Û
то П1 || П2 Û  = 0,
= 0,  = 0.
= 0.
Задача 17. Исследовать взаимное расположение плоскости и прямой, если
а) плоскость задана общим уравнением, прямая – параметрическими уравнениями;
б) плоскость и прямая заданы общими уравнениями.
Плоскость и прямая в прямоугольной системе координат
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Дано: 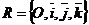 , М0(х0, у0, z0), , М0(х0, у0, z0),  , , 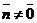 , П ' М0, П ^ , П ' М0, П ^ 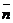 . Найти уравнение П. Решение. М Î П Û либо . Найти уравнение П. Решение. М Î П Û либо 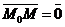 , либо , либо 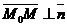 Û Û  . Так как . Так как 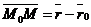 , то М Î П Û , то М Î П Û 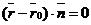 (47) Это векторное уравнение данной плоскости. (47) Это векторное уравнение данной плоскости. |  Рис. 48 Рис. 48 |
Переходя к координатам, получим А(х - х0) + В(у - у0) + С(z - z0) = 0/ (48)
Можно показать, что если плоскость задана в ПДСК общим уравнением (45), то вектор  перпендикулярен этой плоскости.
перпендикулярен этой плоскости.
