Прямая в аффинной системе координат на плоскости и в пространстве
Уравнения прямой, проходящей через данную точку параллельно данному вектору
На плоскости Дано:R = 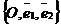 , М0(х0, у0), , М0(х0, у0), 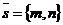 , , 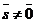 , l 'M0, l ½½ , l 'M0, l ½½  . Найти условие, определяющее l. Пусть М(х, у). . Найти условие, определяющее l. Пусть М(х, у). 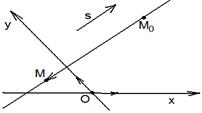 Рис. 33 М Î l Û Рис. 33 М Î l Û 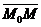 коллинеарен коллинеарен  Û либо 1) Û либо 1) 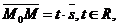 либо 2) координаты либо 2) координаты 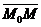 и и  пропорциональны. Рассмотрим оба случая. 1) М Î l Û пропорциональны. Рассмотрим оба случая. 1) М Î l Û 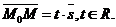 Если Если 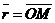 , , 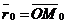 , то получим , то получим 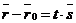 (14) Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору. Перепишем в координатах. Получим (14) Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору. Перепишем в координатах. Получим 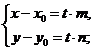 Отсюда Отсюда 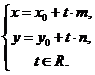 (15) В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору. 2) М Î l Û координаты (15) В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору. 2) М Î l Û координаты 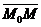 и и  пропорциональны Û пропорциональны Û 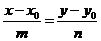 (16). Это каноническое уравнение прямой, проходящей через данную точку параллельно данному вектору. (16). Это каноническое уравнение прямой, проходящей через данную точку параллельно данному вектору. | В пространстве Дано:R = 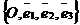 , М0(х0, у0, z0), , М0(х0, у0, z0), 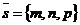 , , 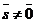 , l 'M0, l ½½ , l 'M0, l ½½  . Найти условие, определяющее l. Пусть М(х, у, z). . Найти условие, определяющее l. Пусть М(х, у, z). 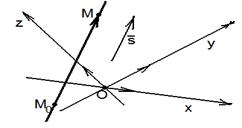 Рис. 331 М Î l Û Рис. 331 М Î l Û 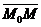 коллинеарен коллинеарен  Û либо 1) Û либо 1) 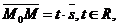 либо 2) координаты либо 2) координаты 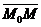 и и  пропорциональны. Рассмотрим оба случая. 1) М Î l Û пропорциональны. Рассмотрим оба случая. 1) М Î l Û 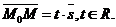 Если Если 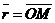 , , 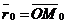 , то получим , то получим 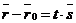 (141) Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору. Перепишем в координатах. Получим (141) Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору. Перепишем в координатах. Получим 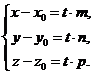 Отсюда Отсюда 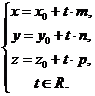 (151) В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору. 2) М Î l Û координаты (151) В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору. 2) М Î l Û координаты 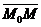 и и  пропорциональны Û пропорциональны Û 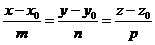 (161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору. (161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору. |
Уравнения прямой, проходящей через две точки
На плоскости Дано:R = 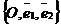 , М1(х1, у1), М2(х2, у2), М1 ¹ М2; l 'M1, l 'M2. Найти уравнения l. Так как М1 ¹ М2, то , М1(х1, у1), М2(х2, у2), М1 ¹ М2; l 'M1, l 'M2. Найти уравнения l. Так как М1 ¹ М2, то 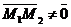 и l ½½ и l ½½ 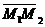 . Следовательно, можно использовать уравнения (15) и (16). Получим . Следовательно, можно использовать уравнения (15) и (16). Получим 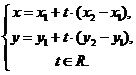 (17) Это параметрические уравнения прямой, проходящей через две точки. Из уравнения (16) получим (17) Это параметрические уравнения прямой, проходящей через две точки. Из уравнения (16) получим 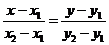 (18) Это каноническое уравнение прямой, проходящей через две точки. (18) Это каноническое уравнение прямой, проходящей через две точки. | В пространстве Дано:R = 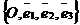 , М1(х1, у1,z1), М2(х2, у2, z2), М1 ¹ М2; l 'M1, l 'M2. Найти уравнения l. Так как М1 ¹ М2, то , М1(х1, у1,z1), М2(х2, у2, z2), М1 ¹ М2; l 'M1, l 'M2. Найти уравнения l. Так как М1 ¹ М2, то 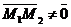 и l½½ и l½½ 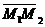 . Следовательно, можно использовать уравнения (151) и (161). Из уравнений (151) получим . Следовательно, можно использовать уравнения (151) и (161). Из уравнений (151) получим 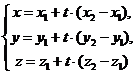 (171) t ÎR. Это параметрические уравнения прямой, проходящей через две точки. Из уравнения (161) следует (171) t ÎR. Это параметрические уравнения прямой, проходящей через две точки. Из уравнения (161) следует 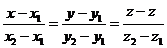 (181). Это канонические уравнения прямой, проходящей через две точки. (181). Это канонические уравнения прямой, проходящей через две точки. |
Общие уравнения прямой
Из уравнений (16) и (18) видно, что любую прямую на плоскости можно задать уравнением первой степени с двумя переменными. Возникает обратный вопрос: всякое ли уравнение первой степени с двумя переменными задаёт в аффинной системе координат на плоскости некоторую прямую? Аналогично, уравнения (161) и (181) эквивалентны системе двух независимых уравнений первой степени с тремя переменными. Поэтому возникает обратная задача: Любая ли система двух независимых уравнений первой степени с тремя переменными задаёт в аффинной системе координат в пространстве прямую?
I.Общее уравнение прямой на плоскости
Дано: R = 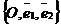 и уравнение Ах + Ву + С = 0, где из коэффициентов А и В хотя бы один отличен от нуля.
и уравнение Ах + Ву + С = 0, где из коэффициентов А и В хотя бы один отличен от нуля.
Показать, что данное уравнение определяет прямую.
Доказательство. Пусть В ¹ 0. При х0 = 0 из данного уравнения получаем у0 = 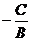 . Вектор
. Вектор 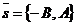 не нулевой, поэтому существует и только одна прямая l такая, что l ' М0, где М0(х0, у0) и l ½½
не нулевой, поэтому существует и только одна прямая l такая, что l ' М0, где М0(х0, у0) и l ½½  . Запишем уравнение l, используя (16). Получим
. Запишем уравнение l, используя (16). Получим 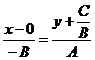 . После преобразования Ах + Ву + С = 0. Получили данное уравнение. Следовательно, оно задаёт прямую.
. После преобразования Ах + Ву + С = 0. Получили данное уравнение. Следовательно, оно задаёт прямую.
Уравнение Ах + Ву + С = 0 называется общее уравнение прямой на плоскости. При этом из доказательства следует, что вектор 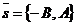 параллелен этой прямой.
параллелен этой прямой.
