Определение и свойства векторов
Определение 1. Геометрический отрезок называется ориентированным, если указан порядок его концов.
Определение 2. Вектором (геометрическим вектором) называется ориентированный отрезок. При этом начало и конец ориентированного отрезка называются соответственно началом и концом вектора. Длина ориентированного отрезка называется длиной вектора.
Вектор обозначается 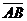 , где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают
, где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают  . Длина вектора обозначается
. Длина вектора обозначается  или
или  . Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают
. Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают 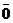 . Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.
. Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.
Определение 3. Два вектора называются равными, если они либо оба нулевые, либо имеют одинаковые длину и направление.
Равенство векторов обладает следующими очевидными свойствами: 1) рефлексивность (всякий вектор равен сам себе); 2) симметричность ( если 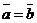 , то
, то  ); 3) транзитивность (если
); 3) транзитивность (если 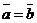 и
и  , то
, то  ).
).
Множество всех равных векторов можно задать 1) одним из векторов (ориентированным отрезком); 2) упорядоченной парой точек; 3) длиной и направлением (в случае ненулевого вектора).
Пусть даны вектор  и точка А. Если и точка А. Если 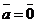 , то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор , то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор  (т.е. В = А). Если (т.е. В = А). Если  , то существует и только один луч, сонаправленный с вектором , то существует и только один луч, сонаправленный с вектором  . На этом луче существует и только одна точка В, расстояние от которой до точки А равно . На этом луче существует и только одна точка В, расстояние от которой до точки А равно  . Но тогда . Но тогда  |  Рис. 1 Рис. 1 |
(рис. 1). Будем говорить, что вектор  отложен от точки А. Итак, любой вектор можно отложить от любой точки и только единственным образом.
отложен от точки А. Итак, любой вектор можно отложить от любой точки и только единственным образом.
Сложение векторов
Пусть  и и  - любые два вектора. Чтобы к вектору - любые два вектора. Чтобы к вектору  прибавить вектор прибавить вектор  нужно отложить вектор нужно отложить вектор  от любой точки А ( от любой точки А ( 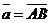 ), от конца В полученного вектора отложить вектор ), от конца В полученного вектора отложить вектор  ( ( 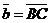 ). Тогда вектор ). Тогда вектор 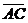 будет вектором суммы, т.е. будет вектором суммы, т.е. 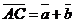 . Иными словами, . Иными словами, 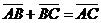 . Свойства сложения векторов. . Свойства сложения векторов. | 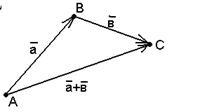 Рис. 2 Рис. 2 |
10. Для любых двух векторов их сумма определена и однозначна. (Следует из определения).
20. 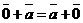 =
=  для любого вектора
для любого вектора  . (Докажите).
. (Докажите).
30. Для любого вектора  существует противоположный вектор (-
существует противоположный вектор (-  ) такой, что
) такой, что  + (-
+ (-  ) =
) = 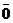 . (Докажите).
. (Докажите).
40. 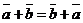 для любых векторов
для любых векторов  и
и  .
.
Доказательство. В случае, когда хотя бы один из векторов нулевой, утверждение следует из предыдущего свойства. Остаётся рассмотреть ненулевые векторы. При этом возможны следующие случаи.
а) Векторы  и и  не параллельны. Пусть не параллельны. Пусть  + +  = = 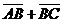 . Отложим от точки А вектор . Отложим от точки А вектор  , пусть , пусть 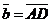 . Так как . Так как 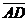 и и 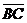 имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Следовательно, имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Следовательно, | 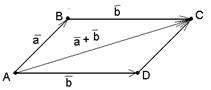 Рис. 3 Рис. 3 |
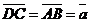 . По правилу сложения векторов
. По правилу сложения векторов 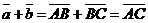 и
и 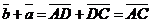 . Отсюда
. Отсюда 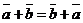 .
.
б) Векторы  и и  параллельны и одинаково направлены (сонаправлены). В этом случае при откладывании от точки А получим параллельны и одинаково направлены (сонаправлены). В этом случае при откладывании от точки А получим 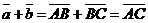 , , 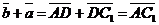 (рис.4). Векторы (рис.4). Векторы 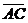 и и 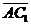 сонаправлены с вектором сонаправлены с вектором  , , |  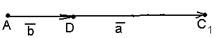 Рис. 4 Рис. 4 |
поэтому сонаправлены между собой. Очевидно, 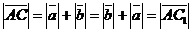 . Следовательно,
. Следовательно, 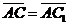 , т.е.
, т.е. 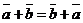 .
.
в) Случай, когда векторы  и
и  параллельны и противоположно направлены, рассмотрите самостоятельно.
параллельны и противоположно направлены, рассмотрите самостоятельно.
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
Очевидно, два вектора неколлинеарны тогда и только тогда, когда они ненулевые и не параллельные. Из случая а) проведённого доказательства следует ещё одно правило сложения неколлинеарных векторов:
Чтобы сложить два неколлинеарных вектора, достаточно отложить их от одной точки, построить на них, как на сторонах, параллелограмм, тогда диагональ этого параллелограмма, идущая из данной точки, будет задавать вектор суммы.
50. 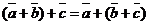 для любых векторов для любых векторов 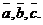 Доказательство. Для левой части получим Доказательство. Для левой части получим 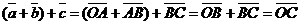 . Для правой части . Для правой части 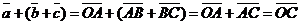 . Результаты равны. . Результаты равны. | 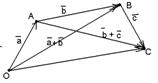 Рис. 5 Рис. 5 |
Определение 5.Разностью упорядоченной пары векторов называется сумма первого вектора и вектора, противоположного второму, т.е.
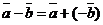 .
.
| Чтобы вычесть из одного вектора второй, достаточно отложить оба вектора от одной точки. Тогда вектор, соединяющий концы полученных отрезков и направленный в сторону уменьшаемого, будет вектором разности (рис. 5). Очевидно, это правило не зависит от того, будут ли векторы коллинеарными или неколлинеарными. Свойства разности: | 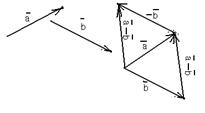 Рис. 6 Рис. 6 |
10. Для любой упорядоченной пары векторов их разность определена и однозначна.
20. Разность двух векторов антикоммутативна.
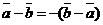 для любых векторов
для любых векторов  и
и  .
.
30. Не выполняется ассоциативный закон, а именно
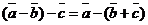 для любых векторов
для любых векторов  ,
,  и
и 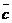 .
.
Задача 1. АВСDA1B1C1D1 - параллелепипед, 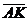 =
= 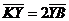 ,
, 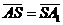 ,
, 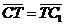 ,
,

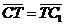 , , 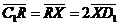 , , 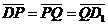 , , 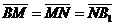 . Найдите 1) . Найдите 1) 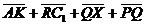 ; 2) ; 2) 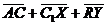 . Решение. 1)Так как . Решение. 1)Так как 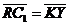 , , 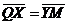 , , 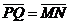 , то , то 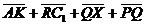 = = 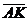 + + 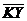 + + 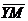 + + 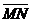 = = 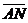 . 2) Так как . 2) Так как 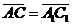 и и 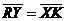 , то , то 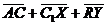 = = 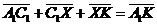 . . | 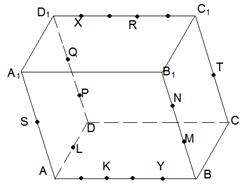 Рис. 7 Рис. 7 |
