Решение системы дифференциальных уравнений первого порядка методом Рунге-Кутты

Система обыкновенных дифференциальных уравнений высшего порядка путем введения новых неизвестных может быть сведена к системе уравнений первого порядка. Рассмотрим такую систему

y_i ' = F_i (x, y)(26)

где i = 1, ..., n;

y = (y1 , y2 , ..., yn );

y(x0 ) = y (0) =(y (0)1 , ..., y (0)n ).

Методе Рунге-Кутта четвертого порядка вычисляет значение y_i ^k по формуле:

y_i^(k+1) = y_i ^(k) + (k₁⁽ⁱ⁾+2×k₂⁽ⁱ⁾+2×k₃⁽ⁱ⁾+k₄⁽ⁱ⁾)/6 (27)

где:

k₁⁽ⁱ⁾ = F_i (x ^(k), y ^(k))×h

k₂⁽ⁱ⁾ = F_i (x^(k)+h/2, y^(k)+k₁⁽ⁱ⁾/2)×h

k₃⁽ⁱ⁾ = F_i (x^(k)+h/2, y^(k)+k₂⁽ⁱ⁾/2)×h

k₄⁽ⁱ⁾ = F_i (x^(k)+h, y^(k)+k₃⁽ⁱ⁾)×h,

h = (x_n -x₀)/m

n – количество уравнений системы, m – количество шагов интегрирования. Процедура использует набор функций F(i, x, y), которые соответствуют функциям F_i (x, y), описанным выше.

Описание алгоритма метода Рунге-Кутты решения систем дифференциальных уравнений первого порядка:

Задаем начальное x₀ и конечное x_n значения отрезка интегрирования, массив начальных значений y₀, т.е. значения системы y0(i)… y0(n) в точке x₀, а также количество шагов интегрирования m.

Вычисляем шаг интегрирования h.

Задаем цикл по х от x₀ до x_n с шагом h.

На основе известных x₀ и y0(1)… y0(n)вычисляем правые части системы для всех n уравнений.

Вычисляем коэффициенты k₁ и для всех n уравнений.

Вычисляются коэффициенты k₂, k_3, k₄ для всех n уравнений системы в соответствии с формулами метода.

Вычисляем y₁… y_т для первого шага интегрирования в соответствии с главной формулой метода.

Итерации повторяются для вычисления состояний системы на каждом шаге интегрирования.

Конец цикла по х.

Конец алгоритма.

Описание алгоритма метода Рунге-Кутты решения системы дифференциальных уравнений первого порядка 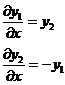с начальными условиями 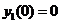, 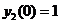при x изменяющемся от 0 до 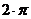на естественном языке:

n=количество_уравнений

y0=начальной_значение

m=количество_шагов_интегрирования

Определить Массив y(m)

Цикл по i от 1 до m с шагом 1

y(1)=0

y(2)=1

Конец Цикла

Вызвать runge_sys(0,2*PI(),@y,m,n)

Процедура runge_sys

Параметры xn,xe,y0,m,n

Определить Массив y0(m)

Определить Локальный Массив k1(m),k2(m),k3(m),k4(m),y1(m),y0_(m),f(m)

Локальные переменные i,x0,h

h=(xe-xn)/(n-1) * шаг интегрирования

Цикл по x0 от xn до xe с шагом h

Вызвать правые_части(x0,@y0,@f,m)

Цикл по i от 1 до m

k1(i)=h*f(i)

y0_(i) = y0(i)+k1(i)/2

Конец Цикла

Вызвать правые_части(x0+h/2,@y0_,@f,m)

Цикл по i от 1 до m

k2(i)=h*f(i)

y0_(i) = y0(i)+k2(i)/2

Конец Цикла

Вызвать правые_части(x0+h/2,@y0_,@f,m)

Цикл по i от 1 до m

k3(i)=h*f(i)

y0_(i) = y0(i)+k3(i)

Конец Цикла

Вызвать правые_части(x0+h,@y0_,@f,m)

Цикл по i от 1 до m

k4(i)=h*f(i)

dk=1/6*(k1(i)+2*k2(i)+2*k3(i)+k4(i))

y1(i)=y0(i)+dk

Конец Цикла

Вызвать вывод_решения(x0+h,@y1,m)

Цикл по i от 1 до m

y0(i) = y1(i)

Конец Цикла

Конец Цикла

Возврат

Конец Процедуры

Процедура правые_части

Параметры x,y,f,n

Определить Массив y(n),f(n)

f(1)=y(2)

f(2)=-y(1)

Возврат

Конец Процедуры

Процедура вывод_решения

Параметры x,y,m

Определить Массив y(m)

Печать x,STR(y(1),10,7),STR(f(x),10,7),STR(ABS(y(1)-f(x)),10,7)

Возврат

Конец Процедуры

Функция f

Параметры x

Возврат SIN(x)

Конец Функции

Реализация алгоритма численного интегрирования системы дифференциальных уравнений первого порядка методом Рунге-Кутта на VFP:

set decimals to 10

clear

n=100

y0=0.5

m=2

DIMENSION y(m)

y(1)=0

y(2)=1

s=""

runge_sys(0,2*PI(),@y,m,n)

STRTOFILE(s,"res.dat")

PROCEDURE runge_sys

PARAMETERS xn,xe,y0,m,n

DIMENSION y0(m)

LOCAL ARRAY k1(m),k2(m),k3(m),k4(m),y1(m),y0_(m),f(m)

LOCAL i,x0,h

h=(xe-xn)/(n-1)

FOR x0 = xn TO xe STEP h

правые_части(x0,@y0,@f,m)

FOR i=1 TO m

k1(i)=h*f(i)

y0_(i) = y0(i)+k1(i)/2

NEXT

правые_части(x0+h/2,@y0_,@f,m)

FOR i=1 TO m

k2(i)=h*f(i)

y0_(i) = y0(i)+k2(i)/2

NEXT

правые_части(x0+h/2,@y0_,@f,m)

FOR i=1 TO m

k3(i)=h*f(i)

y0_(i) = y0(i)+k3(i)

NEXT

правые_части(x0+h,@y0_,@f,m)

FOR i=1 TO m

k4(i)=h*f(i)

dk=1/6*(k1(i)+2*k2(i)+2*k3(i)+k4(i))

y1(i)=y0(i)+dk

NEXT

s= s + вывод_решения(x0+h,@y1,m) + CHR(10)

FOR i=1 TO m

y0(i) = y1(i)

NEXT

NEXT

RETURN

PROCEDURE правые_части

LPARAMETERS x,y,f,n

DIMENSION y(n),f(n)

*? "x=",x

f(1)=y(2)

f(2)=-y(1)

RETURN

ENDPROC

PROCEDURE вывод_решения

PARAMETERS x,y,m

LOCAL s

DIMENSION y(m)

s = STR(x,12,2) + CHR(9) ;

+ STR(y(1),10,7) + CHR(9) ;

+ STR(y(2),10,7) + CHR(10)

RETURN s

ENDPROC

Реализация алгоритма численного интегрирования системы дифференциальных уравнений первого порядка методом Рунге-Кутты на VBA:

Sub runge_sys()

Const PiNumber = 3.14159265358979

Dim y()

Dim k1(), k2(), k3(), k4(), y1(), y_tmp(), f()

dec = 8

n = 100

m = 2 * n

x1 = 0: xn = 2 * PiNumber

ReDim k1(m): ReDim k2(m): ReDim k3(m): ReDim k4(m)

ReDim y1(m): ReDim y_tmp(m): ReDim f(m)

ReDim y(m)

Debug.Print "X Y F(x) ABS(Y-F(x))"

For i = 1 To m Step 2

y(i) = 0

y(i + 1) = 1

Next i

h = (xn - x1) / (n - 1)

For x0 = x1 To xn Step h

Call правые_части(x0, y(), f, m)

For i = 1 To m

k1(i) = h * f(i)

y_tmp(i) = y(i) + k1(i) / 2

Next i

Call правые_части(x0 + h / 2, y_tmp, f, m)

For i = 1 To m

k2(i) = h * f(i)

y_tmp(i) = y(i) + k2(i) / 2

Next i

Call правые_части(x0 + h / 2, y_tmp, f, m)

For i = 1 To m

k3(i) = h * f(i)

y_tmp(i) = y(i) + k3(i)

Next i

Call правые_части(x0 + h, y_tmp, f, m)

For i = 1 To m

k4(i) = h * f(i)

dk = 1 / 6 * (k1(i) + 2 * k2(i) + 2 * k3(i) + k4(i))

y1(i) = y(i) + dk

Next i

Call вывод_решения(x0 + h, y1, m, dec)

For i = 1 To m

y(i) = y1(i)

Next i

Next x0

End Sub

Sub правые_части(x, y, f, n)

'Debug.Print "x=", x

For i = 1 To 200 Step 2

f(i) = y(i + 1)

f(i + 1) = -y(i)

Next i

End Sub

Sub вывод_решения(x, y, m, dec)

dStr = "0."

For i = 1 To dec

dStr = dStr + "0"

Next i

Debug.Print Format(x, dStr), Format(y(1), dStr), Format(f(x), dStr), Format(Abs(y(1) - f(x)), dStr)

'Return

End Sub

Function f(x)

f = Sin(x)

End Function

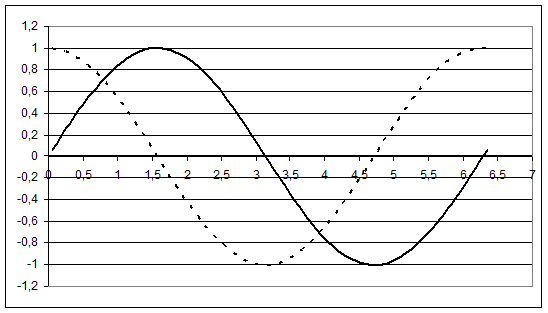
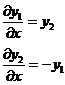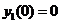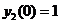Рис. 1 График решения системы дифференциальных уравнений при , на интервале x = 0 до 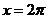. Сплошная линия – зависимость 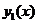, пунктирная - .

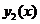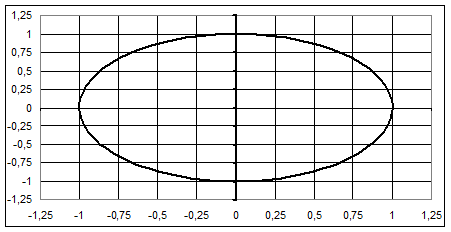
Рис.2 Фазовый портрет 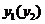решения системы дифференциальных уравнени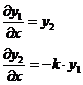й при 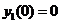, 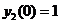на интервале x = 0 до 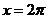. По горизонтальной оси 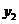по вертикальной оси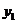

Контрольные вопросы

1. Какое уравнение называется дифференциальным?

2. Что называется обыкновенным дифференциальным уравнением?

3. Что называется уравнением в частных производных?

4. Что называется порядком дифференциального уравнения?

5. Что называется решением дифференциального уравнения?

6. Что называется интегрированием дифференциального уравнения?

7. Что называется задачей Коши?

8. Что называется краевой задачей?

9. Что называется общим решением дифференциального уравнения?

10. Что такое интегральные кривые?

11. Что такое однородное дифференциальное уравнение первого порядка?

12. Что такое линейное дифференциальное уравнение первого порядка?

13. Запишите вид динамической системы дифференциальных уравнений.

14. Что называется фазовым пространством?

15. Что называется фазовой траекторией?

16. Что называется линейной системой дифференциальных уравнений?

17. Запишите вид линейной системы дифференциальных уравнений с постоянными коэффициентами.

18. Запишите вид характеристического уравнения линейной однородной системы дифференциальных уравнений.

Задания

Решить методами Эйлера, Кранка-Николсона и Рунге-Кутты одно из следующих уравнений вида y' = F(x,y) на интервале [x₀,x_n] с начальным условием y(x₀)=y₀, принимая h = 0,01.

	y' = F(x,y)	[x0,xn]	y(x0)
№1.	y' = x2+y;	[0; 0,2];	y0 = 1.
№2.	y' = 2x2+y;	[0; 0,2];	y0 = 1.
№3.	y' = 2x+y;	[0; 0,2];	y0 = 1.
№4.	y' = x+2y;	[0; 0,2];	y0 = 1.
№5.	y' = x2–y;	[1; 1,2];	y0 = 0.
№6.	y' = x–2y;	[1; 1,2];	y0 = 0.
№7.	y' = 2(x+y);	[1; 1,2];	y0 = 0.
№8.	y' = 2x–3y;	[1; 1,2];	y0 = 0.
№9.	y' = 2x+3y;	[0; 0,2];	y0 = 1.
№10.	y' = x+3.5 y;	[0; 0,2];	y0 = 1.
№11.	y' = 4x+y;	[0; 0,2];	y0 = 1.
№12.	y' = 3x–y;	[0; 0,2];	y0 = 1.
№13.	y' = 4x–y;	[0; 0,2];	y0 = 1.
№14.	y' = 1+xy;	[1; 1,5];	y0 = 1.
№15.	y' = x+y;	[0; 0,5];	y0 = 1.
№16.	y' = 2x+y;	[0; 0,5];	y0 = 1.
№17.	y' = 3x+y;	[0; 0,5];	y0 = 1.
№18.	y' = 4x+y;	[0; 0,5];	y0 = 1.
№19.	y' = y–2x;	[0; 0,5];	y0 = 1.
№20.	y' = y–3x;	[0; 0,5];	y0 = 1.
№21.	y' = x+y2;	[0; 0,5];	y0 = 1.
№22.	y' = x–y2;	[1; 1,5];	y0 = 0.
№23.	y' = x–2y2;	[1; 1,5];	y0 = 0.
№24.	y' = 2x–y2;	[1; 1,5];	y0 = 0.

Решите методами Эйлера, Кранка-Николсона и Рунге-Кутты систему дифференциальных уравнений и постройте графики решений и фазовые портреты:

1. Для диссипативной колебательной системы (с силой сопротивления пропорциональной скорости)

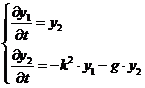
при различных значениях коэффициентов k и g.

2. Для колебательной системы с зависящим от времени положением равновесия

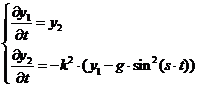
при различных значениях коэффициентов k, g и s. Начальные условия и диапазон решения определите самостоятельно.

3. Для диссипативной колебательной системы с внешней силой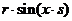

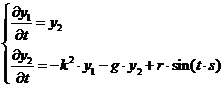
при различных значениях коэффициентов k, g, r и s. Начальные условия и диапазон решения определите самостоятельно.