Метод Рунге-Кутты четвертого порядка для решения уравнения первого порядка

При решении дифференциального уравнения или системы дифференциальных уравнений численными методами решение определяется всегда с определенной погрешностью. Наиболее грубым методом с большой погрешностью является метод Эйлера, точность определения решения этим методом пропорциональна шагу сетки. Метод Кранка-Николсона дает более точное решение, погрешность этого метода пропорциональна квадрату шага сетки. Таким образом, метод Эйлера является методом первого порядка точности, метод Кранка-Николсона относится к методам второго порядка точности. Существует общий подход позволяющий получать вычислительные схемы для решения дифференциальных уравнений более высоких порядков точности – третьего, четвертого и так далее. Такие схемы, основанные на разложении решения в ряд Тейлора, называются методами Рунге-Кутты. Так, схема Рунге-Кутты второго порядка имеет вид:

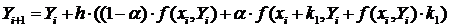
где

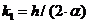
При 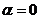получаем схему Эйлера, при 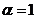получаем схему Рунге-Кутты 2-го порядка точности.

Схема метода Рунге-Кутты третьего порядка точности может быть записана в виде:

,

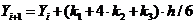где:

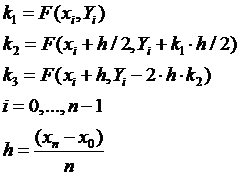
Наиболее употребительным методом Рунге-Кутты решения дифференциальных уравнений является метод Рунге-Кутты четвертого порядка (при котором погрешность определения решения пропорциональна четвертой степени шага), в котором вычисления производятся по формуле:

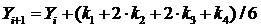, (13)

где:

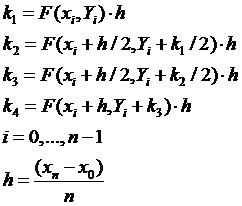(14)

Описание алгоритма метода Рунге-Кутты для решения дифференциального уравнения первого порядка:

Задаем начальное x₀ и конечное x_n значения отрезка интегрирования, начальное y₀, т.е. значение функции y в точке x₀, а также количество шагов интегрирования n.

Вычисляем величину шага интегрирования h.

Цикл по х от х₀ до х_n с шагом h .

Вычисляем k1 = F(x , y )×h.

Вычисляем x1 = x +h/2.

Вычисляем Y1 = Y +K1/2.

Вычисляем k2 = F(x1,y1)×h.

Вычисляем k2 = F(x1,y1)×h.

Вычисляем Y2 = Y+K2/2.

Вычисляем k3 = F(x1,y2)×h.

Вычисляем x4 = x+h.

Вычисляем y4 = Y+K3.

Вычисляем k4 = F(x4,y4)×h.

Вычисляем Y = Y +(k1 +2×k2 +2×k3 +k4 )/6.

Конец цикла.

Определить функцию F(x,y).

Задать вид функции F(x,y).

Конец функции.

Алгоритм метода Рунге-Кутты 4-го порядка для решения дифференциального уравнения первого порядка на естественном языке:

х₀ = значение_левой_границы

х_n = значение_правой_границы

Y = начальное_значение_функции

n=количество_шагов_интегрирования

h = (x_n-x₀)/n

Цикл по x от x₀ до x_n с шагом h

k1 = F(x , y )*h

x1 = x +h/2

Y1 = Y +K1 /2

k2 = F(x1,y1)*h

Y2 = Y+K2 /2

k3 = F(x1,y2)*h

x4 = x+h

y4 = Y+K3

k4 = F(x4,y4)*h

Y = Y +(k1 +2*k2 +2*k3 +k4 )/6

Конец Цикла

Определение Функции F

Параметры x,y

F=… *** задается вид функции

Конец Функции

Приведем примеры реализации метода Рунге-Кутты для ранее рассмотренного уравнения (см. метод Эйлера) и сравним точность вычислений методом Эйлера и Рунге-Кутты.

Пример реализация алгоритма численного интегрирования дифференциального уравнения первого порядка на VFP для уравнения (5):

CLEAR

x0 = 0

xn = 1

y0 = 1

n = 10

Dimension x(n+1), y(n+1)

runge(x0, xn, y0, @x, @y, n)

?"Решение: X(i) Тестовые Y_test(i) Вычисленные Y(i) Delta(Y_test(i)-Y(i))"

For i = 1 To n

delta=ABS(f_test(x(i))-y(i))

?STR(x(i),12,3),STR(y(i),20,16),STR(f_test(x(i)),20,16),STR(delta,20,16)

Next i

procedure runge

LPARAMETERS x0, xn, y0, x, y, n

DIMENSION x(n+1),y(n+1)

local i, h, dk

h = (xn - x0) / n

k1 = h * f(x0, y0)

k2 = h * f(x0 + h / 2, y0 + k1 / 2)

k3 = h * f(x0 + h / 2, y0 + k2 / 2)

k4 = h * f(x0 + h, y0 + k3)

dk = 1 / 6 * (k1 + 2 * k2 + 2 * k3 + k4)

y(1) = y0 + dk

x(1) = x0 + h

For i = 1 To n

k1 = h * f(x(i), y(i))

k2 = h * f(x(i) + h / 2, y(i) + k1 / 2)

k3 = h * f(x(i) + h / 2, y(i) + k2 / 2)

k4 = h * f(x(i) + h, y(i) + k3)

dk = 1 / 6 * (k1 + 2 * k2 + 2 * k3 + k4)

y(i + 1) = y(i) + dk

x(i + 1) = x(i) + h

Next i

ENDPROC

Function F(x, y)

F=y

RETURN F

EndFunc

Function f_test(fx)

f_test=EXP(fx)

RETURN f_test

EndFunc

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка методом Рунге-Кутты на VBA (для макроса MS’Excel) для уравнения (5):

Sub Test_Runge_Kytt()

Dim x(), y()

x0 = 0: xn = 1

y0 = 1

n = 100

ReDim y(n + 1): ReDim x(n + 1)

Call runge(0, 1, y0, x(), y(), n)

For i = 1 To n

ActiveSheet.Cells(i, 1).Value = x(i)

ActiveSheet.Cells(i, 2).Value = y(i)

y_test = f_test(x(i))

delta_y = Abs(y_test - y(i))

Debug.Print "x= " & Format(x(i), "0.000") & " : y= " & Format(y(i), "0.000 000 000 000") & " : y_test= " _

& Format(y_test, "0.000 000 000 000") & " : delta_y= " & Format(delta_y, "0.000 000 000 000")

Next i

End Sub

Sub runge(x0, xn, y0, x(), y(), n)

Dim i, h, dk

h = (xn - x0) / n

k1 = h * f(x0, y0)

k2 = h * f(x0 + h / 2, y0 + k1 / 2)

k3 = h * f(x0 + h / 2, y0 + k2 / 2)

k4 = h * f(x0 + h, y0 + k3)

dk = 1 / 6 * (k1 + 2 * k2 + 2 * k3 + k4)

y(1) = y0 + dk

x(1) = x0 + h

For i = 1 To n

k1 = h * f(x(i), y(i))

k2 = h * f(x(i) + h / 2, y(i) + k1 / 2)

k3 = h * f(x(i) + h / 2, y(i) + k2 / 2)

k4 = h * f(x(i) + h, y(i) + k3)

dk = 1 / 6 * (k1 + 2 * k2 + 2 * k3 + k4)

y(i + 1) = y(i) + dk

x(i + 1) = x(i) + h

Next i

End Sub

Function f(x, y)

f = y

End Function

Function f_test(x)

f_test = Exp(x)

End Function

Результаты работы программы на VBA:

x=0,10:y=1,105 170 833 333:y_test=1,105 170 918 076:delta_y=0,000 000 084 742

x=0,20:y=1,221 402 570 851:y_test=1,221 402 758 160:delta_y=0,000 000 187 309

x=0,30:y=1,349 858 497 063:y_test=1,349 858 807 576:delta_y=0,000 000 310 513

x=0,40:y=1,491 824 240 081:y_test=1,491 824 697 641:delta_y=0,000 000 457 561

x=0,50:y=1,648 720 638 597:y_test=1,648 721 270 700:delta_y=0,000 000 632 103

x=0,60:y=1,822 117 962 092:y_test=1,822 118 800 391:delta_y=0,000 000 838 299

x=0,70:y=2,013 751 626 597:y_test=2,013 752 707 470:delta_y=0,000 001 080 874

x=0,80:y=2,225 539 563 292:y_test=2,225 540 928 492:delta_y=0,000 001 365 200

x=0,90:y=2,459 601 413 780:y_test=2,459 603 111 157:delta_y=0,000 001 697 377

x=1,00:y=2,718 279 744 135:y_test=2,718 281 828 459:delta_y=0,000 002 084 324

В данной реализации все значения вычисляемой функции и ее аргумента хранятся в массивах.