Лабораторная работа №9. Численное решение дифференциальных уравнений

Методы численного решения дифференциальных уравнений первого порядка

Дифференциальным уравнением первого порядка называют уравнение вида:

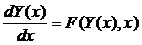. (1)

При численном решении дифференциального уравнения первого порядка вида (1) с начальным условием Y(x₀) = y₀ (задача Коши) сначала выбираем фиксированное приращение аргумента h = (x_n -x₀ )/n, где x₀ – начальная точка интервала интегрирования, x_n - конечная точка интервала интегрирования, n – число шагов. Далее, используя один из итерационных методов численного интегрирования дифференциальных уравнений первого порядка, находим значение Y(x_n).

Метод Эйлера

Метод Эйлера относится к наиболее простым базовым методам решения дифференциальных уравнений. Этот метод основан на представлении производной в конечно-разностной форме:

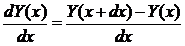(2)

Так, для дифференциального уравнения вида (1) при достаточно малых значениях приращения аргумента x, можно, представив производную в виде отношения приращения функции к приращению аргумента, получить следующее приближенное представление в виде конечно-разностного уравнения:

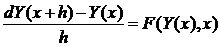(3)

Из этого представления легко выразить «новое» значение функции (значение функции в точке x+h) – расчетную формулу метода Эйлера:

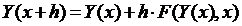(4)

Описание алгоритма численного интегрирования дифференциального уравнения первого порядка методом Эйлера:

Задаем начальное x₀ и конечное x_n значения отрезка интегрирования, начальное y₀, т.е. значение функции y в точке x₀, а также количество шагов интегрирования n.

Вычисляем величину шага интегрирования h = (x_n -x₀ )/n.

Задаем цикл по k от 2 до n+1.

В цикле, на основе значения x_k-1 вычисляем x_k, т.е. x₁ = x₀+ h, x₂ = x₁+ h и т.д.

В цикле на основе значения Y_k-1 по рекуррентной формуле вычисляем y_k, т.е. Y₁=Y₀+h*F(x₀,Y₀), Y₂=Y₁+h*F(x₁,Y₁) и т.д. Значение F(x_k,Y_k) должно вычисляться в функции, соответствующей правой части дифференциального уравнения. Конец цикла.

Конец алгоритма.

Алгоритм численного интегрирования дифференциального уравнения первого порядка методом Эйлера на естественном языке:

x0=начальное_значение_х

xn=конечное_значение_х

y0=начальное_значение_Y

n=количество_шагов_интегрирования

h=(xn-x0)/n

Определить Массив X(n+1)

Определить Массив Y(n+1)

X(1)=x0

Y(1)=y0

Цикл по i от 2 до n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*F(X(i-1),Y(i-1))

Конец Цикла

Печать " Решение: Значения х Значения Y(х) :"

Цикл по i от 1 до n+1

Печать X(i),Y(i)

Конец Цикла

Определить Функцию F

Параметры x,y

f=.... *** Задается вид функции

Вернуть f

Конец Определения Функции

Покажем пример реализации метода Эйлера на примере уравнения

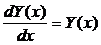, т.е. 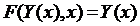(5)

При аналитическом интегрировании данного уравнения получаем начальное значение функции в точке x₀=0 и вид искомой функции:

, .

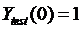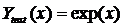Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка методом Эйлера на VFP для уравнения (5):

SET DECIMALS TO 8

CLEAR

* Начальное и конечное значения х

x0=0

xn=1

* Начальное значение y

y0=1

* Количество итераций

n=10

h=(xn-x0)/n

DIMENSION X(n+1),Y(n+1)

X(1)=x0

Y(1)=y0

*Y(i+1)=Y(i)+h*F(X(i),Y(i))

FOR i=2 TO n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*F(X(i-1),Y(i-1))

ENDFOR

? " Решение :”

? " Значения Х Известные значения Y Вычисленные значения Y :"

FOR i=1 TO n+1

?X(i),F_test(X(i)),Y(i)

ENDFOR

function F

lPARAMETERS x,y

f=y

RETURN f

ENDFUNC

function F_test

lPARAMETERS x

F_test=EXP(x)

RETURN F_test

ENDFUNC

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка методом Эйлера на VBA для уравнения (5):

Sub Euler_Test()

' Начальное и конечное значения х

x0 = 0

xn = 1

' Начальное значение y

y0 = 1

' Количество итераций

n = 10

h = (xn - x0) / n

ReDim x(n + 1)

ReDim y(n + 1)

x(1) = x0

y(1) = y0

'Y(i+1)=Y(i)+h*F(X(i),Y(i))

For i = 2 To n + 1

x(i) = x(i - 1) + h

y(i) = y(i - 1) + h * F(x(i - 1), y(i - 1))

Next i

Debug.Print "РЕШЕНИЕ :"

Debug.Print "Значения Х Известные значения Y Вычисленные значения Y"

For i = 1 To n + 1

Debug.Print x(i), F_test(x(i)), y(i)

Next i

End Sub

Function F(x, y)

F = y

End Function

Function F_test(x)

F_test = Exp(x)

End Function

Результат работы программы:

РЕШЕНИЕ :

Значения Х Известные значения Y Вычисленные значения Y

0 1 1

0,1 1,10517091807565 1,1

0,2 1,22140275816017 1,21

0,3 1,349858807576 1,331

0,4 1,49182469764127 1,4641

0,5 1,64872127070013 1,61051

0,6 1,82211880039051 1,771561

0,7 2,01375270747048 1,9487171

0,8 2,22554092849247 2,14358881

0,9 2,45960311115695 2,357947691

1 2,71828182845905 2,5937424601

Метод Кранка-Николсона

Метод Кранка-Николсона представляет собой модификацию метода Эйлера, в которой правая часть разностной формы дифференциального уравнения представляется в виде среднего значения правой части в точке x и правой части в точке x+h:

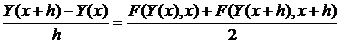(6)

Поскольку искомое значение функции в точке x+h присутствует и в левой и в правой части уравнения – эта формула содержит Y(x+h) неявно, поэтому, для получения расчетной формулы необходимо выразить Y(x+h) явно. Выразить явно Y(x+h) возможно не для любого вида F(Y(x),x). Метод Кранка-Николсона можно применять, tсли правая часть дифференциального уравнения зависит только от x, т.е. F(Y(x),x)=F(x).

Рассмотрим пример дифференциального уравнения с разрешимой правой частью, зависящей от x и Y(x):

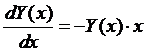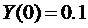, (7)

Запишем разностный вид этого дифференциального уравнения:

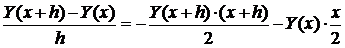
После простых преобразований:

1) ,

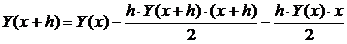2) ,

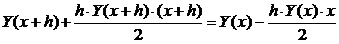3) .

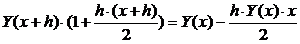Получим расчетную формулу:

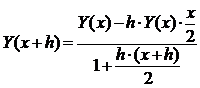. (8)

В случае, когда правая часть дифференциального уравнения зависит только от х, формула метода Кранка-Николсона имеет вид:

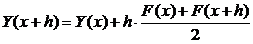(9)

Например, для дифференциального уравнения с правой частью, зависящей только от x:

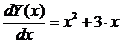(10)

формула Кранка-Николсона имеет вид:

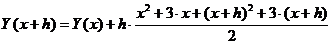. (11)

Описание алгоритма численного интегрирования дифференциального уравнения первого порядка с правой частью уравнения, зависящей только от х, методом Кранка-Николсона:

Задаем начальное x₀ и конечное x_n значения отрезка интегрирования, начальное y₀, т.е. значение функции y в точке x₀, а также количество шагов интегрирования n.

Вычисляем величину шага интегрирования h.

Задаем цикл по k от 2 до n+1.

В цикле на основе значения x_k-1 вычисляем x_k, т.е. x₁ = x₀+ h, x₂ = x₁+ h и т.д.

В цикле на основе значения Y_k-1 по рекуррентной формуле вычисляем y_k, т.е. Y₁=Y₀+h*(F(x₀,Y₀)+F(x₁,Y₁))/2, Y₂=Y₁+h*(F(x₁,Y₁)+F(x₂,Y₂))/2 и т.д. Значение F(x_k,Y_k) должно вычисляться в функции, соответствующей правой части дифференциального уравнения. Конец цикла.

Конец алгоритма.

Алгоритм численного интегрирования дифференциального уравнения первого порядка с правой частью уравнения, зависящей только от х, методом Кранка-Николсона на естественном языке:

x0=начальное_значение_х

xn=конечное_значение_х

y0=начальное_значение_Y

n=количество_шагов_интегрирования

h=(xn-x0)/n

Определить Массив X(n+1)

Определить Массив Y(n+1)

X(1)=x0

Y(1)=y0

Цикл по i от 2 до n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*(F(X(i-1),Y(i-1))+ F(X(i),Y(i)))/2

Конец Цикла

Печать " Решение: Значения х Значения Y(х) :"

Цикл по i от 1 до n+1

Печать X(i),Y(i)

Конец Цикла

Определить Функцию F

Параметры x,y

f=.... *** Задается вид функции

Вернуть f

Конец Определения Функции

Покажем пример реализации метода Кранка-Николсона на примере уравнения (10). При аналитическом интегрировании уравнения (10) получаем начальное значение функции в точке x₀=0 и вид искомой функции:

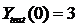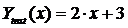, . (12)

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка с правой частью, зависящей только от х, методом Кранка-Николсона на VFP для уравнения (10):

SET DECIMALS TO 8

CLEAR

* Начальное и конечное значения х

x0=0

xn=1

* Начальное значение y

y0=3

* Количество итераций

n=10

h=(xn-x0)/n

DIMENSION X(n+1),Y(n+1)

X(1)=x0

Y(1)=y0

*Y(i+1)=Y(i)+h*F(X(i),Y(i))

FOR i=2 TO n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*F(X(i-1),Y(i-1))

ENDFOR

? " Решение :"

? " Значения Х Известные значения Y Вычисленные значения Y :"

FOR i=1 TO n+1

?X(i),F_test(X(i)),Y(i)

ENDFOR

function F

lPARAMETERS x,y

f=x*x+3*x

RETURN f

ENDFUNC

function F_test

lPARAMETERS x

F_test=2*x+3

RETURN F_test

ENDFUNC

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка с правой частью, зависящей только от х, методом Кранка-Николсона на VBA для уравнения (10):

Sub Krank_Nikolson_Test()

' Начальное и конечное значения х

x0 = 0

xn = 1

' Начальное значение y

y0 = 3

' Количество итераций

n = 10

h = (xn - x0) / n

ReDim x(n + 1)

ReDim y(n + 1)

x(1) = x0

y(1) = y0

'Y(x+h) = Y(x) + h*(x^2 + 3*x + (x+h)^2 + 3*(x+h))/2

For i = 2 To n + 1

x(i) = x(i - 1) + h

y(i) = y(i - 1) + h * (F(x(i - 1), y(i - 1)) + F(x(i), y(i))) / 2

Next i

Debug.Print "РЕШЕНИЕ :"

Debug.Print "Значения Х Известные значения Y Вычисленные значения Y"

For i = 1 To n + 1

Debug.Print x(i), F_test(x(i)), y(i)

Next i

End Sub

Function F(x, y)

F = x ^ 2 + 3 * x

End Function

Function F_test(x)

F_test = 2 * x + 3

End Function

Результат работы программы на VBA:

РЕШЕНИЕ :

Значения Х Известные значения Y Вычисленные значения Y

0 3 3

0,1 3,2 3,0155

0,2 3,4 3,063

0,3 3,6 3,1445

0,4 3,8 3,262

0,5 4 3,4175

0,6 4,2 3,613

0,7 4,4 3,8505

0,8 4,6 4,132

0,9 4,8 4,4595

1 5 4,835