Определение корня одномерного уравнения методом простой итерации

Основная расчетная формула метода простой итерации для определения корня уравнения

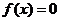(14)
имеет вид:

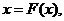(15)

где .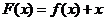

При использовании метода простой итерации корни уравнения 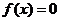располагаются в тех же точках, в которых пересекаются линейная функция 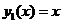, проходящая через начало координат и функция 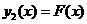. Иными словами корни функции 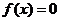соответствуют корням системы уравнений:

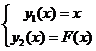(16)

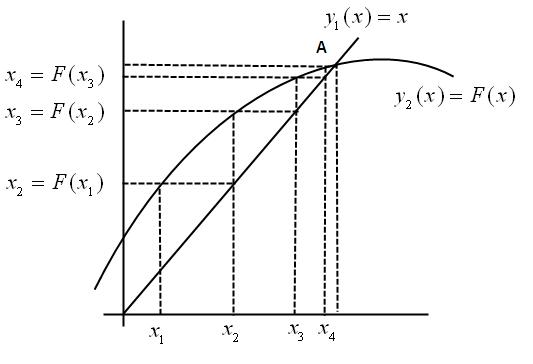
Рис.3 Иллюстрация сходящегося процесса метода простой итерации

На рисунке 3 проиллюстрирован процесс последовательного решения уравнения (1) методом простой итерации. Пересечение кривой 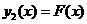и прямой 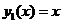(точка A) соответствует решению системы уравнений (16) и корню уравнения (14).

В окрестности корня задается начальное значение аргумента 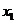, затем по формуле (15) определяется значение 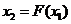– точка пересечения с кривой 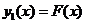, затем, полученное значение 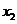также подставляется в формулу (15) и определяется следующее приближение к корню – 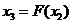. Процесс продолжается до тех пор, пока корень уравнения не будет найден с требуемой точностью T, то есть пока погрешность текущей итерации 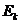не станет меньше точности. Погрешность 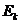определения корня на шаге k может быть оценена, например, как разность текущего и предыдущего значения аргумента: 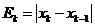. Таким образом, условие завершения итерационного процесса метода простой итерации можно записать следующим образом:

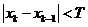(17)
Алгоритм метода простой итерации выглядит следующим образом:

x1=начальное_значение

err = требуемая_точность

Начало цикла

x2=F(x1)

Если |x2-x1| < err тогда

Вывод на печать x2

Выход из программы

Иначе

x1=x2

Конец если

Конец цикла

Метод простой итерации находит корень не во всех случаях. На рисунке 4 приведен пример расходящегося процесса.

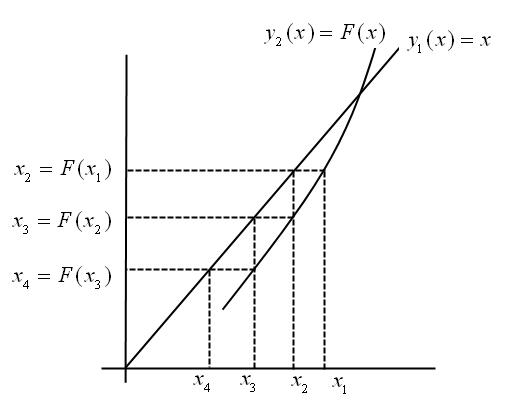
Рис. 4 Пример расходящегося процесса метода простой итерации

Рассмотрим нестрогий вывод условия сходимости метода простой итерации.

В случае сходимости итерационного процесса ряд значений аргумента функции представляет собой сходящуюся последовательность, подобно приведенной на рисунке 5.

Рис. 5 Сходящийся ряд значений x_k

Если ряд 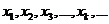сходится, то для него справедливо соотношение:

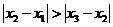(18)
или для шага с номером k

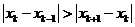(19)
Если правую часть неравенства (19), с учетом (15), представить в виде 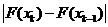, тогда условие сходимости на шаге k принимает вид:

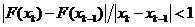(20)

Условие сходимости метода простой итерации (20) представляет собой разностное представление производной функции 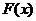, таким образом, из формулы (20) можно получить дифференциальную форму условия сходимости метода простой итерации:

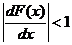(21)
для значений 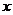, принадлежащих окрестности искомого корня.

Формулу (21) можно использовать для предварительной оценки сходимости метода простой итерации. Так, для примера, приведенного на рис.3, производная функции 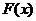в окрестности корня меньше единицы – процесс сходится, а для примера, приведенного на рис.4 производная функции 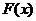в окрестности корня больше единицы и процесс расходится.

В некоторых случаях можно улучшить сходимость метода простой итерации. Рассмотрим модифицированный метод простой итерации. Корни уравнения 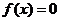не изменятся, если к правой и левой части добавить 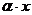, где 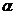– параметр (в более общем случае к правой и левой части уравнения (14) можно добавить произвольную обратимую функцию 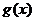). Тогда уравнение (14) примет вид:

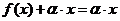
выразив 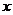, получим новую усовершенствованную формулу для метода простой итерации:

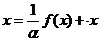
или

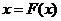, где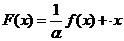

Условие сходимости (20) для модифицированного метода простой итерации будет иметь вид следующего неравенства с параметром :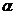

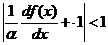
или

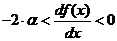(22)
Изменяя параметр 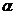в выражении (22) можно значительно улучшить сходимость метода простой итерации.

В качестве примера рассмотрим процесс определения корней уравнения .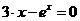

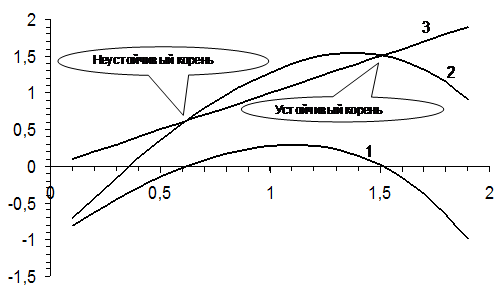
Рис. 6 Анализ функции 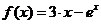для метода простой итерации

На рисунке 6 приведены графики функции 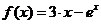– линия 1, 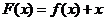– линия 2, 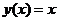– линия 3. Поскольку тангенс угла наклона линии 2 больше чем 1 в окрестности первого корня – этот корень неустойчив. Второй корень устойчив – тангенс угла наклона линии 2 в окрестности второго корня меньше единицы.

Описание алгоритма нахождения корня нелинейного одномерного уравнения методом простой итерации:

Задаем точность вычисления корня по оси абсцисс и по оси ординат: e_x и e_y.

Задаем максимальное количество итераций нахождения корня – maxi.

Задаем начальное значение x₀.

Начало цикла по i от 1 до maxi.

В цикле вычисляем следующее приближение корня: x₁=f(x₀)+x₀.

В цикле вычисляем изменение значений x и f(x) на данной итерации:

dx=|x₁-x₀|, df=|f(x₁)-f(x₀)|.

Проверяем условие сходимости алгоритма. Задаем ветвление: если dx<e_x и df<e_y, то корень найден, вывод на экран значения x_i, f(x_i)иномера итерации i. Выход из программы. Конец ветвления.

Копируем значение x₁ в x₀ для следующей итерации: x₀=x₁.

Конец цикла.

Вывод сообщения: ”Корень не найден за i итераций”

Конец программы.

Описание алгоритма нахождения корня уравнения 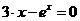методом простой итерации на естественном языке:

ex=точность_по_оси_X

ey=точность_по_оси_Y

maxi=максимальное_количество_итераций

x0=начальное_значение_х

Цикл по i от 1 до maxi

x1=f(x0)

dx=Модуль(x1-x0)

df=Модуль(f(x1)-f(x0))

Если dx<ex И df<ey Тогда

Печать " Корень найден за "+i+" итераций "

Печать " x= "+x1+" f(x)= "+f(x1)

Печать " Конец итераций "

Выход Из Программы

Конец Если

x0=x1

Конец Цикла

Печать "Решение не найдено за "+ maxi +"итераций "

Определение Функции f0

Параметры x

Возврат 3*x-EXP(x)

Конец Определения Функции

Определение Функции f

Параметры x

Возврат f0(x)+x

Конец Определения Функции

Пример реализации алгоритма нахождения корня одномерного нелинейного уравнения 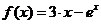методом простой итерации на VFP:

CLEAR

ex=0.0001

ey=0.0001

maxi=100

x0=1

FOR i=1 TO maxi

x1=f(x0)

dx=ABS(x1-x0)

df=abs(f(x1)-f(x0))

IF dx<ex AND df<ey then

?" Корень найден за "+ALLTRIM(STR(i))+" итераций "

?" x= "+STR(x1)+" f(x)= "+STR(f(x1))

?

?" Конец итераций "

RETURN

ENDIF

x0=x1

endfor

? "Решение не найдено за", maxi, "итераций"

FUNCTION f0

PARAMETERS x

RETURN 3*x-EXP(x)

ENDFUNC

FUNCTION f

PARAMETERS x

RETURN f0(x)+x

ENDFUNC

Пример реализации алгоритма нахождения корня одномерного нелинейного уравнения 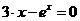методом простой итерации на VBA:

Sub Simple_Iteration()

ex = 0.0001

ey = 0.0001

maxi = 100

x0 = 1.1

For i = 1 To maxi

x1 = f(x0) + x0

df = Abs(f(x1) - f(x0))

Debug.Print "i=" & i & " x= " & x1 & " f(x)= " & f(x1)

If Abs(x1 - x0) < ex And df < ey Then

Debug.Print " Корень найден за " & i & " итераций"

Debug.Print " x= " & x1 & " f(x)= " & f(x1)

Debug.Print " Конец итераций"

Exit Sub

End If

x0 = x1

Next i

Debug.Print "Решение не найдено за", maxi, "итераций"

End Sub

Function f0(x)

f = 2*x - Exp(x)

End Function

Function f(x)

f = f0(x)+x

End Function

Результаты работы программы на VBA для функции 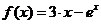, начального значения x₀ = 1.1:

i=1 x= 1,39583397605357 f(x)= 0,149160879773209

i=2 x= 1,54499485582678 f(x)= -5,29629438655936E-02

i=3 x= 1,49203191196118 f(x)= 2,99752635717079E-02

i=4 x= 1,52200717553289 f(x)= -0,01539014343569

i=5 x= 1,5066170320972 f(x)= 8,40821312260687E-03

i=6 x= 1,51502524521981 f(x)= -4,46024377229914E-03

i=7 x= 1,51056500144751 f(x)= 2,40587791438962E-03

i=8 x= 1,5129708793619 f(x)= -1,28652386385397E-03

i=9 x= 1,51168435549804 f(x)= 6,91223382955464E-04

i=10 x= 1,512375578881 f(x)= -3,70446886386766E-04

i=11 x= 1,51200513199461 f(x)= 1,98802854120217E-04

i=12 x= 1,51220393484873 f(x)= -1,06611507514565E-04

i=13 x= 1,51209732334122 f(x)= 5,71945781615568E-05

i=14 x= 1,51215451791938 f(x)= -3,06771414297913E-05

Корень найден за 14 итераций

x= 1,51215451791938 f(x)= -3,06771414297913E-05

Контрольные вопросы

1. Что такое корень уравнения?

2. Что такое непрерывность и гладкость функции?

3. Дайте определение разрывной функции, приведите примеры разрывных и непрерывных функций.

4. Дайте определение монотонности функции, приведите примеры монотонности и немонотонности.

5. Приведите условие наличия корня монотонной функции на заданном отрезке.

6. Определите понятия точность и погрешность нахождения корней уравнения.

7. Как определяются точность и погрешность нахождения корней уравнения в методе деления отрезка пополам?

8. Приведите определение итерационной процедуры.

9. В чем заключается итерационная процедура метода деления отрезка пополам?

10. Приведите условие завершения итераций в методе деления отрезка пополам.

11. Приведите условие применимости метода секущих.

12. Как определяется точность и погрешность нахождения корней уравнения в методе секущих.

13. Дайте определение понятию «разностная производная».

14. Выведите основные формулы метода секущих.

15. Приведите алгоритм итерационной процедуры метода секущих.

16. В чем состоит условие завершения итераций в методе секущих?

17. При каких условиях применим метод простой итерации?

18. Как определяется точность и погрешность нахождения корней в методе простой итерации?

19. Приведите алгоритм итерационной процедуры метода простой итерации.

20. Выведите условие сходимости метода простой итерации.

21. Выведите модифицированную формулу метода простой итерации.

22. Опишите алгоритм модифицированного метода простой итерации.

Задания

Найти корни одного из следующих уравнений, используя методы: простой итерации, деления отрезка пополам, касательных и секущих.

1. ln x + (x + 1)³ = 0;

2. x×2^x = 1;

3. x – cos x = 0;

4. 3x + cos x + 1 = 0;

5. x + lg x = 0,5;

6. 2 – x = ln x;

7. (2 – x)×e^x = 0;

8. 2,2×x – 2^x = 0;

9. x² + 4 sin x = 0;

10. 2x – lg x = 7;

11. 5x – 8 ln x = 8;

12. 3×x – e^x = 0;

13. x (x + 1)² = 1;

14. x = (x + 1)³;

15. x² = sin x;

16. x³ = sin x;

17. x² = ln (x+1);

18. 2x + lg x = – 0,5;

19. 2x + cos x = 0,5;

20. sin 0,5x +1 = x²; x>0;

21. 0,5x + lg (x–1) = 0,5;

22. sin (0,5 + x) = 2x – 0,5;

23. lg (2 + x) +2x = 3;

24. lg (1 + 2x) = 2 – x;

25. 2 sin (x – 0,6) = 1,5 – x.