Определение корня уравнения методом деления отрезка пополам (дихотомии)
Корнем уравнения называется точка координат, в которой функция обращается в ноль (меняет свой знак). Для одномерной функции f=f(x) корнем будет являться точка x0 при условии f(x0)=0.
Метод деления отрезка пополам или метод дихотомии – один из наиболее распространенных простейших итерационных методов нахождения корней нелинейных уравнений. Во всех итерационных методах корни функции находятся приближенно при помощи многократных повторений вычислительной процедуры, пока не будет достигнута требуемая точность. Если после каждого повторения (итерации) погрешность в вычислении корня уменьшается – то итерационная процедура сходится (происходит приближение к корню), иначе – процесс расходится.
Для использования метода деления отрезка пополам необходимо предварительно проанализировать поведение функции, например, протабулировать фунуцию, выделить окрестности корней и выбрать тот корень, который следует найти первым – т.е. задать отрезок [a, b], в котором расположен корень. Значения функции на концах отрезка [a, b] будут иметь разные знаки. Делим начальный отрезок пополам – на отрезки [a, х0] и [х0, b], где х0=(a+b)/2. Для отрезка с корнем значения функции f(x) в граничных точках будут иметь разные знаки. Обозначаем через a и b границы этого отрезка. В качестве критерия того, что функция имеет разные знаки, можно использовать знак произведения на концах отрезка двух функций – f(a)*f(b). Если произведение f(a)*f(b) будет меньше нуля, то функция в точках a и b имеет разные знаки. Второй отрезок, на котором знак f(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем точку х0. Проверяем значение функции f(х0), если оно по модулю меньше заданной точности – e, т.е. |f(х0)|<e , то считаем, что корень найден. Если корень с допустимой погрешностью еще не найден, то переходим ко второй итерации – снова делим этот отрезок пополам, находим новую точку х1=(a+b)/2 и повторяем итерационную процедуру.
В качестве критериев сходимости можно использовать анализ текущей ширины отрезка [a, b] и модуля значения функции |f(х0)|. Если текущая ширина отрезка [a, b] становится меньше допустимой погрешности e: [a,b]<e и модуль значения функции |f(х0)| меньше заданной точности e: |f(х0)|<e, то процесс прекращается – корень найден.
Для того чтобы в случае расходимости метода вычисления не длились бесконечно долго максимальное количество итераций ограничивают. Как правило, для определения корня достаточно нескольких десятков итераций.
Описание алгоритма нахождения корня уравнения методом деления отрезка пополам:
Задаем начальные параметры: точность нахождения корня – e, максимальное количество итераций – max_i.
Задаем границы отрезка a и b, на котором должен находиться корень (для увренности в том, что корень действительно существует на данном отрезке можно протабулировать функцию на отрезке [a,b]).
Проверяем, если на заданном отрезке функция меняет знак, то продолжаем вычисления, в обратном случае печатаем сообщение «отрезок выбран неудачно» и завершаем работу программы.
Задаем цикл от 1 до максимального количества итераций max_i.
Находим середину отрезка [a,b] – точку х0, вычисляем значение функции в этой точке.
Если данная точка является корнем функции с заданной точностью, то печатаем найденное значение корня и завершаем работу программ, в обратном случае проверяем знаки функции в точке х0 и в точке а.
Если знаки функции различны – корень функции находится внутри отрезка [a,х0] – переносим правый конец отрезка – точку b в точку середины отрезка – х0: b=х0 и переходим на начало цикла.
Если знаки функции на границах отрезка [a,х0] одинаковые – корень функции находится в правой половине исходного отрезка – [х0,b]. В этом случае переносим левую границу исходного отрезка – точку a в точку х0: a=х0 и переходим на начало цикла.
Алгоритм нахождения корня уравнения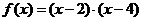 
методом деления отрезка пополам на естественном языке:
e=точность_вычисления_корня
maxi=максимальное_количество_итераций
a=левая_граница_отрезка
b=правая_граница_отрезка
Цикл по i от 1 до maxi
fa=f(a)
fb=f(b)
Если fa*fb<0 Тогда
x=(a+b)/2
fx=f(x)
Печать i, x, fx
Если Модуль(fx)<e
Печать " Корень найден, x= "+x
Печать " за "+i+ " итераций "
Выход из программы
Иначе
Если fa*fx<0 Тогда
b=x
Конец Если
Если fx*fb<0 Тогда
a=x
Конец Если
Конец Если
Иначе
Печать i,fa,fb
Печать" Отрезок [a,b] выбран неудачно "
Конец Если
Конец Цикла
Печать "Решение не найдено за", maxi, "итераций"
Определить Функцию f
Параметры x
Возврат (x-4)*(x-2)
Конец Определения Функции
Здесь и далее запись Модуль(fx) означает вызов стандартной функции вычисления абсолютного значения аргумента fx.
Пример реализации алгоритма решения на языке VFP:
clear
e=0.001
maxi=1000
input "Введите границу отрезка а: " to a
input "Введите границу отрезка b: " to b
FOR i=1 TO maxi
fa=f(a)
fb=f(b)
IF fa*fb<0 then
x=(a+b)/2
fx=f(x)
?" Итерация= "+ALLTRIM(STR(i))
??" : x= " +alltrim(str(x,12,2))
??" : (f(x))= "+ alltrim(str(f(x),12,2))
IF ABS(fx)<e
?" Корень найден, x= "+ALLTRIM(str(x))
??" за "+ALLTRIM(STR(i))+ " итераций "
RETURN
ELSE
IF fa*fx<0
b=x
endif
IF fx*fb<0
a=x
endif
ENDIF
ELSE
? " Итерация= "+ALLTRIM(STR(i))
? " Отрезок ["
?? alltrim(str(a,12,2))
?? ", "
?? alltrim(str(b,12,2))
?? "] выбран неудачно "
return
ENDIF
ENDFOR
? "Решение не найдено за", maxi, "итераций"
FUNCTION f
PARAMETERS x
RETURN (x-4)*(x-2)
ENDFUNC
Пример реализации алгоритма решения задачи на VBA:
Sub Dichotomia()
e = 0.001
maxi = 1000
a = Val(InputBox("Введите границу отрезка а: "))
b = Val(InputBox("Введите границу отрезка b: "))
For i = 1 To maxi
fa = f(a)
fb = f(b)
If fa * fb < 0 Then
x = (a + b) / 2
fx = f(x)
Debug.Print " Итерация= " + CStr(i)
Debug.Print " x= " + Format(x, "00.00")
Debug.Print " (f(x))= " + Format(fx, "00.0000")
If Abs(fx) < e Then
Debug.Print "Конец работы программы "
Debug.Print " Корень найден, x= " + CStr(x)
Debug.Print " За " + CStr(i) + " итераций "
solution = True
Exit Sub
Else
If fa * fx < 0 Then
b = x
End If
If fx * fb < 0 Then
a = x
End If
End If
Else
Debug.Print " Итерация= " + CStr(i)
Debug.Print " : f(a)= " + Format(fa, "00.0000")
Debug.Print " : f(b)= " + Format(fb, "00.0000")
Debug.Print " Отрезок [a,b] выбран неудачно "
Exit Sub
End If
Next i
If Not solution Then Debug.Print "Решение не найдено за", maxi, "итераций"
End Sub
Function f(x)
f = (x - 4) * (x - 2)
End Function
Результаты работы программы на VBA для отрезка а=0, b=3:
---Табуляция функции---
x= 00,00 : f(x)= 08,0000
x= 00,50 : f(x)= 05,2500
x= 01,00 : f(x)= 03,0000
x= 01,50 : f(x)= 01,2500
x= 02,00 : f(x)= 00,0000
x= 02,50 : f(x)= -00,7500
x= 03,00 : f(x)= -01,0000
-----------------------
Итерация= 1
x= 01,50
(f(x))= 01,2500
Итерация= 2
x= 02,25
(f(x))= -00,4375
Итерация= 3
x= 01,88
(f(x))= 00,2656
Итерация= 4
x= 02,06
(f(x))= -00,1211
Итерация= 5
x= 01,97
(f(x))= 00,0635
Итерация= 6
x= 02,02
(f(x))= -00,0310
Итерация= 7
x= 01,99
(f(x))= 00,0157
Итерация= 8
x= 02,00
(f(x))= -00,0078
Итерация= 9
x= 02,00
(f(x))= 00,0039
Итерация= 10
x= 02,00
(f(x))= -00,0020
Итерация= 11
x= 02,00
(f(x))= 00,0010
Конец работы программы
Корень найден, x= 1,99951171875
За 11 итераций