Сложение и вычитание алгебраических дробей с разными знаменателями

Пример 2.Сложить дроби: .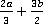

Решение:

Алгоритм решения абсолютно аналогичен предыдущему примеру. Легко подобрать общий знаменатель данных дробей: 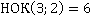и дополнительные множители для каждой из них.

.

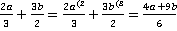Ответ: .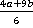

Итак, сформулируем алгоритм сложения и вычитания алгебраических дробей с разными знаменателями:

1. Найти наименьший общий знаменатель дробей.

2. Найти дополнительные множители для каждой из дробей (поделив общий знаменатель на знаменатель данной дроби).

3. Умножив на полученные множители, привести дроби к общему знаменателю.

4. Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.

Рассмотрим теперь пример с дробями, в знаменателе которых присутствуют буквенные выражения.

Пример 3.Сложить дроби: .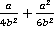

Решение:

Поскольку буквенные выражения в обоих знаменателях одинаковы, то следует найти общий знаменатель для чисел 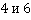. Итоговый общий знаменатель будет иметь вид: 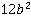. Таким образом, решение данного примера имеет вид:

.

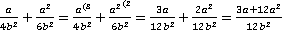Ответ: .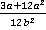

Пример 4.Вычесть дроби: .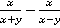

Решение:

Если «схитрить» при подборе общего знаменателя не удаётся (нельзя разложить на множители или воспользоваться формулами сокращённого умножения), то в качестве общего знаменателя приходится брать произведение знаменателей обеих дробей.

.

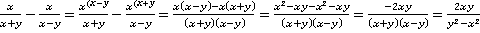Ответ: .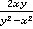

Вообще, при решении подобных примеров, наиболее сложным заданием является нахождение общего знаменателя.

Пример вычитания алгебраических дробей с разложением знаменателя на множители

Рассмотрим более сложный пример.

Пример 5.Упростить: .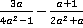

Решение:

При нахождении общего знаменателя необходимо прежде всего попытаться разложить знаменатели исходных дробей на множители (чтобы упростить общий знаменатель).

В данном конкретном случае:

;

.

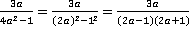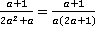Тогда легко определить общий знаменатель: .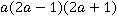

Определяем дополнительные множители и решаем данный пример:

.

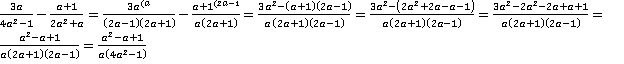Ответ: .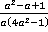

Примеры на закрепление правил сложения и вычитания алгебраических дробей с разными знаменателями

Теперь закрепим правила сложения и вычитания дробей с разными знаменателями.

Пример 6.Упростить: .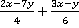

Решение:

.

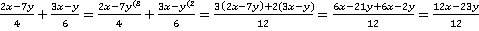Ответ: .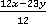

Пример 7.Упростить: .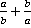

Решение:

.

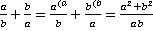Ответ: .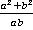

Пример сложения трёх алгебраических дробей с разными знаменателями

Рассмотрим теперь пример, в котором складываются не две, а три дроби (ведь правила сложения и вычитания для большего количества дробей остаются такими же).

Пример 8.Упростить: .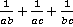

Решение:

.

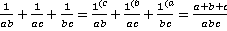Ответ: .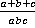

6. Пример вычитания алгебраических дробей с предварительным сокращением

Теперь рассмотрим пример, в котором необходимо сначала сократить дроби, а затем уже их складывать (вычитать).

Пример 9.Упростить: .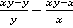

Решение:

Рассмотрим первую дробь:

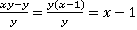. При этом следует указать, что .

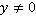Проведём аналогичные преобразования со второй дробью:

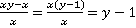. При этом следует указать, что .

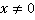Таким образом, получаем следующее преобразование:

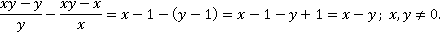
Ответ: .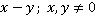

На данном уроке мы рассмотрели правила сложения и вычитания дробей с разными знаменателями, а также решили типовые несложные задачи с использованием этих правил. В дальнейшем мы рассмотрим более сложные примеры задач на эти правила.

Домашнее задание

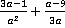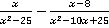1. Упростить выражение: а) , б) , в) .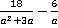

2. Вычислить значение выражения 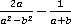при .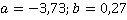

3. Упростить выражение .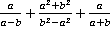

Урок 12:Сло­же­ние и вы­чи­та­ние ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми (более слож­ные слу­чаи).

Урок яв­ля­ет­ся про­дол­же­ни­ем преды­ду­ще­го за­ня­тия, и на нем более глу­бо­ко и по­дроб­но рас­смат­ри­ва­ет­ся тех­ни­ка сло­же­ния и вы­чи­та­ния ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми. В на­ча­ле урока при­во­дит­ся несколь­ко при­ме­ров на по­вто­ре­ние сло­же­ния и вы­чи­та­ния дро­бей в про­стых слу­ча­ях, а затем боль­шое вни­ма­ние уде­ля­ет­ся за­да­чам по­вы­шен­ной слож­но­сти. В них рас­смат­ри­ва­ет­ся при­ме­не­ние уме­ния рас­кла­ды­вать мно­го­чле­ны на мно­жи­те­ли раз­лич­ны­ми спо­со­ба­ми для на­хож­де­ния наи­мень­ше­го об­ще­го зна­ме­на­те­ля дро­бей.

1. По­вто­ре­ние сло­же­ния/вы­чи­та­ния обык­но­вен­ных дро­бей с раз­ны­ми зна­ме­на­те­ля­ми

На уроке мы про­дол­жим тему преды­ду­ще­го урока и будем рас­смат­ри­вать за­да­чу сло­же­ния и вы­чи­та­ния ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми, т.е. упро­ще­ние вы­ра­же­ний вида: 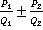, где 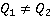. В ос­нов­ном, за­да­ча сво­дит­ся к на­хож­де­нию наи­мень­ше­го об­ще­го зна­ме­на­те­ля дро­бей, а это де­ла­ет­ся, как мы уже знаем, по ана­ло­гии с обык­но­вен­ны­ми дро­бя­ми. Рас­смот­рим при­ме­ры.

При­мер 1.Вы­пол­нить дей­ствие .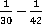

Ре­ше­ние.Для на­хож­де­ния наи­мень­ше­го об­ще­го зна­ме­на­те­ля дро­бей вос­поль­зу­ем­ся ос­нов­ной тео­ре­мой ариф­ме­ти­ки и раз­ло­жим зна­ме­на­те­ли на про­стые мно­жи­те­л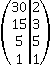и.

и 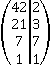. Сле­до­ва­тель­но, 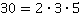и .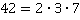

Вспом­ним, что наи­мень­ший общий зна­ме­на­тель дол­жен со­дер­жать мно­жи­те­ли всех зна­ме­на­те­лей, при­чем так, чтобы мно­жи­те­лей было ми­ни­маль­но воз­мож­ное ко­ли­че­ство. В нашем слу­чае необ­хо­ди­мы мно­жи­те­ли 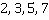. Сле­до­ва­тель­но, общий зна­ме­на­тель 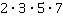, а до­пол­ни­тель­ные мно­жи­те­ли: к пер­вой дроби 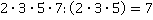, ко вто­рой дроби .

.

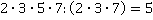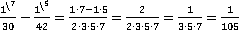Как видно из ре­ше­ния, удоб­но даже не пе­ре­мно­жать про­стые мно­жи­те­ли в зна­ме­на­те­ле до по­лу­че­ния чис­ли­те­ля общей дроби, чтобы потом было легче со­кра­щать дробь.

Ответ. .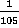

2. При­ме­ры на сло­же­ние/вы­чи­та­ние двух ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми с ис­поль­зо­ва­ни­ем раз­ло­же­ния зна­ме­на­те­лей на мно­жи­те­ли

Те­перь рас­смот­рим ана­ло­гич­ные опе­ра­ции с ал­геб­ра­и­че­ски­ми дро­бя­ми. Не слож­но до­га­дать­ся, что самой тру­до­ем­кой ча­стью сло­же­ния или вы­чи­та­ния дро­бей с раз­ны­ми зна­ме­на­те­ля­ми яв­ля­ет­ся на­хож­де­ние наи­мень­ше­го об­ще­го зна­ме­на­те­ля. Если в слу­чае обык­но­вен­ных дро­бей можно было поль­зо­вать­ся раз­ло­же­ни­ем чисел на мно­жи­те­ли, то в ал­геб­ра­и­че­ских дро­бях на мно­жи­те­ли необ­хо­ди­мо будет рас­кла­ды­вать мно­го­чле­ны. Для этого су­ще­ству­ет несколь­ко из­вест­ных нам ме­то­дов: вы­не­се­ние об­ще­го мно­жи­те­ля, при­ме­не­ние фор­мул со­кра­щен­но­го умно­же­ния и ме­то­да груп­пи­ров­ки сла­га­е­мых. Рас­смот­рим более по­дроб­но их при­ме­не­ние для ре­ше­ния слож­ных задач на сло­же­ние и вы­чи­та­ние ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми.

При­мер 2.Вы­пол­нить дей­ствия .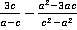

Ре­ше­ние.Для на­хож­де­ния наи­мень­ше­го об­ще­го зна­ме­на­те­ля и до­пол­ни­тель­ных мно­жи­те­лей раз­ло­жим зна­ме­на­те­ли на мно­жи­те­ли. Пер­вый зна­ме­на­тель уже пред­став­ля­ет собой про­стое вы­ра­же­ние, а вто­рой рас­кла­ды­ва­ет­ся по фор­му­ле раз­но­сти квад­ра­тов:

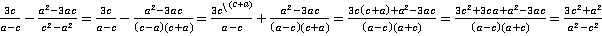. Как видно по ходу ре­ше­ния, в ка­че­стве наи­мень­ше­го об­ще­го зна­ме­на­те­ля вы­бран зна­ме­на­тель вто­рой дроби, ко­то­рый де­лит­ся и на пер­вый зна­ме­на­тель и сам на себя. До­пол­ни­тель­ный мно­жи­тель в таком слу­чае при­го­дил­ся толь­ко для пер­вой дроби. Во вто­ром пе­ре­хо­де можно об­ра­тить вни­ма­ние на вне­се­ние ми­ну­са перед дро­бью в один из мно­жи­те­лей зна­ме­на­те­ля для того, чтобы сде­лать зна­ме­на­те­ли дро­бей мак­си­маль­но по­хо­жи­ми друга на друга; такой прием нам уже зна­ком из темы «сло­же­ние ал­геб­ра­и­че­ских дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми (более слож­ные слу­чаи)» (урок №5).

Ответ. .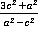

При­мер 3. Вы­пол­нить дей­ствия .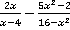

Ре­ше­ние.По­сту­пим ана­ло­гич­но с преды­ду­щим при­ме­ром и раз­ло­жим по ходу ре­ше­ния зна­ме­на­тель вто­рой дроби на мно­жи­те­ли по фор­му­ле раз­но­сти квад­ра­тов, перед этим вне­сем минус перед дро­бью в зна­ме­на­тель для того, чтобы он по­лу­чил более удоб­ный вид:

.

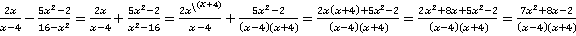Ответ. .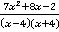

3. При­ме­ры на сло­же­ние/вы­чи­та­ние трех ал­геб­ра­и­че­ских дро­бей с раз­ны­ми зна­ме­на­те­ля­ми с ис­поль­зо­ва­ни­ем раз­ло­же­ния зна­ме­на­те­лей на мно­жи­те­ли

Рас­смот­рим те­перь более слож­ные при­ме­ры на сло­же­ние/вы­чи­та­ние трех дро­бей.

При­мер 4.Вы­пол­нить дей­ствия .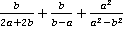

Ре­ше­ние.Как и ранее, раз­ло­жим на мно­жи­те­ли каж­дый зна­ме­на­тель, най­дем наи­мень­ший общий зна­ме­на­тель и до­пол­ни­тель­ные мно­жи­те­ли.

.

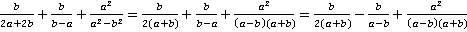Как и ранее, для при­ве­де­ния вы­ра­же­ния к удоб­но­му виду, вы­не­сем минус из зна­ме­на­те­ля вто­рой дроби. По­сколь­ку в вы­ра­же­нии при­сут­ству­ет три дроби, чтобы не за­пу­тать­ся, вы­пи­шем наи­мень­ший общий зна­ме­на­тель от­дель­но, со­ста­вив его из мно­жи­те­лей, вхо­дя­щих во все зна­ме­на­те­ли: 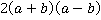. Ис­хо­дя из него, ука­жем и до­пол­ни­тель­ные мно­жи­те­ли для каж­дой из дро­бей, как те мно­жи­те­ли, ко­то­рых не хва­та­ет зна­ме­на­те­лю, чтобы стать общим.

.

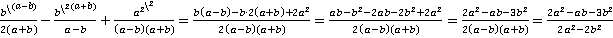По­след­ний пе­ре­ход (рас­кры­ва­ние ско­бок) не прин­ци­пи­а­лен, и можно было ука­зать в ответ вы­ра­же­ние, за­пи­сан­ное пред­по­след­ним.

Ответ. .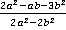

При­мер 5.Вы­пол­нить дей­ствия .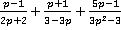

Ре­ше­ние.По­сту­па­ем уже из­вест­ным для нас об­ра­зом: рас­кры­ва­ем зна­ме­на­те­ли на мно­жи­те­ли, при необ­хо­ди­мо­сти ме­ня­ем знаки в зна­ме­на­те­лях дро­бей, на­хо­дим наи­мень­ший общий зна­ме­на­тель и до­пол­ни­тель­ные мно­жи­те­ли.

.

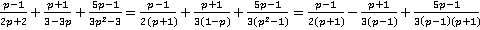Наи­мень­ший общий зна­ме­на­тель: .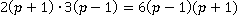

.

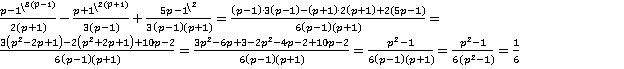Можно за­ме­тить, что вы­ра­же­ние в чис­ли­те­ле 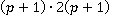пред­ста­ви­мо в виде 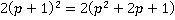по фор­му­ле квад­ра­та суммы, ана­ло­гич­но вы­ра­же­ние .

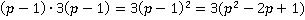В конце про­ве­де­но со­кра­ще­ние на 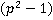, зна­чит необ­хо­ди­мо обя­за­тель­но за­пи­сать об­ласть недо­пу­сти­мых зна­че­ний пе­ре­мен­ной, свя­зан­ную с этим со­кра­ще­ни­ем: 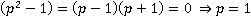и 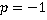яв­ля­ют­ся недо­пу­сти­мы­ми зна­че­ни­я­ми пе­ре­мен­ных. Во всех осталь­ных слу­ча­ях вы­ра­же­ние равно .

Ответ. .

На сле­ду­ю­щем уроке мы по­дроб­но оста­но­вим­ся на тех­ни­ке раз­ло­же­ния на мно­жи­те­ли зна­ме­на­те­лей дро­бей для их по­сле­ду­ю­ще­го сло­же­ния и вы­чи­та­ния. Эта тех­ни­ка чрез­вы­чай­но важна, т.к. мы видим, что она ак­тив­но ис­поль­зу­ет­ся во всех рас­смот­рен­ных ранее опе­ра­ци­ях с дро­бя­ми.

До­маш­нее за­да­ние

1. Вы­пол­нить дей­ствия .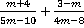

2. Вы­пол­нить дей­ствия .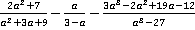

3. До­ка­зать тож­де­ство: .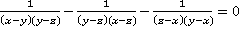

Урок 13:Разложение знаменателя на множители при сложении и вычитании алгебраических дробей

На данном уроке будут рассмотрены различные способы разложения знаменателя на множители при сложении и вычитании алгебраических дробей. Фактически, мы вспомним те методы, которые уже были изучены ранее. Это и вынесение общего множителя за скобки, и группировка слагаемых, и применение формул сокращённого умножения, а также выделение полного квадрата. Все эти методы применяются при сложении и вычитании алгебраических дробей с разными знаменателями. В рамках урока мы вспомним все вышеперечисленные правила, а также разберём примеры на применение этих правил.

1. Общие правила сложения и вычитания дробей с разными знаменателями, примеры

Напомним, что алгебраической дробью называется выражени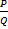е , где 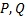– многочлены. А многочлены можно и нужно уметь раскладывать на множители. Предположим, нам необходимо сложить или вычесть две алгебраические дроби: .

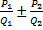Каков алгоритм наших действий?

1. Сократить или упростить каждую из дробей.

2. Найти наименьший общий знаменатель двух дробей.

Эти действия требуют разложения на множители многочленов .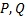

Рассмотрим несколько примеров на сокращение (упрощение) дробей.

Пример 1.Упростить: .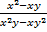

Решение:

Первое, что необходимо попытаться сделать при сокращении, – вынести общий множитель за скобки.

В нашем случае и в числителе, и в знаменателе есть множители, которые можно вынести за скобки.

.

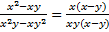Затем сократим общие множители числителя и знаменателя. Получим:

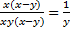. При этом учтём, что знаменатель дроби не может равняться 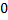. То есть: .

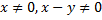Ответ: .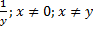

Пример 2.Упростить: .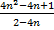

Решение:

По схеме решения предыдущего примера попытаемся вынести за скобки общий множитель. В числителе это сделать нельзя, а в знаменателе можно вынести за скобку .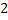

Если не получается вынести общий множитель, нужно попробовать воспользоваться формулами сокращённого умножения. Действительно, в числителе стоит полный квадрат разности. Получаем:

.

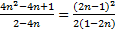Мы видим похожие скобки в числителе и знаменателе.

Однако они отличаются знаком.

Для этого воспользуемся равенством: 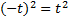. Отсюда получаем: 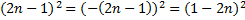. Получаем:

.

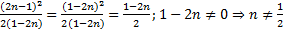Ответ: .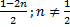

Рассмотрим теперь пример, в котором необходимо упростить разность двух дробей.

Пример 3.Упростить: .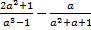

Решение:

Поскольку в знаменателе первой дроби стоит разность кубов, воспользуемся формулой сокращённой умножения. Получаем:

.

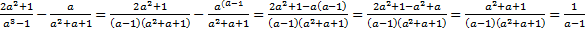Ответ: 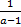.