Алгоритм ортогонализации грама - шмидта

Процесс Грама ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе a₁,a₂,...,a_k строится ортогональная система b₁,b₂,...,b_k такая, что каждый вектор b_i линейно выражается через a₁,a₂,...,a_i, то есть матрица перехода от {a_i} к {b_i} ― верхнетреугольная матрица.

Этот процесс применим также и к счётной системе векторов.

(Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами, что есть частный случай разложения Ивасавы. )

Классический процесс Грама — Шмидта

Алгоритм

Пусть имеются линейно независимые векторы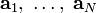

Определим оператор проекции следующим образом: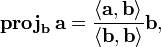

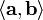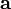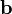где — скалярное произведение векторов и . Этот оператор проецирует вектор 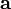ортогонально на вектор .

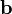Классический процесс Грама — Шмидта выполняется следующим образом:

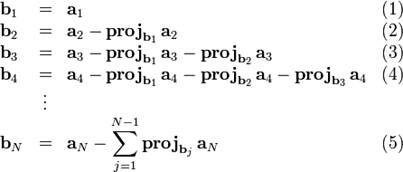
На основе каждого вектора 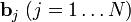может быть получен нормированный вектор: 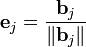(у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).

Результаты процесса Грама — Шмидта:

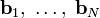— система ортогональных векторов либо

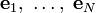— система ортонормированных векторов.

Вычисление 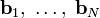носит название ортогонализации Грама — Шмидта, а 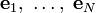— ортонормализации Грама — Шмидта.

Геометрическая интерпретация — вариант 1

Рассмотрим формулу (2) — второй шаг алгоритма. Её геометрическое представление изображено на рис. 1:

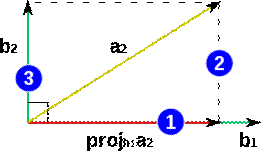
1 — получение проекции вектор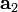а на ;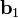

2 — вычисление 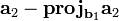, то есть перпендикуляра, которым выполняется проецирование конц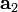а на 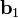. Этот перпендикуляр — вычисляемый в формуле (2) вектор ;

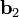3 — перемещение полученного на шаге 2 вектора 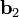в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (2).

На рисунке видно, что вектор 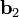ортогонален вектору 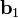, так как является перпендикуляром, по которому 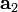проецируется на .

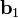Рассмотрим формулу (3) — третий шаг алгоритма — в следующем варианте:

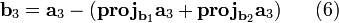
Её геометрическое представление изображено на рис. 2:

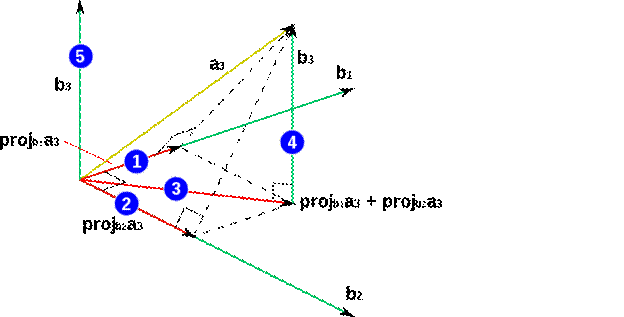
1 — получение проекции вектор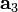а на ;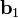

2 — получение проекции вектор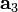а на ;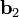

3 — вычисление суммы 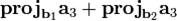, то есть проекции вектора 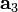на плоскость, образуемую векторам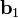и и 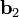. Эта плоскость закрашена на рисунке серым цветом;

4 — вычисление 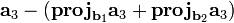, то есть перпендикуляра, которым выполняется проецирование конца 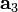на плоскость, образуемую векторам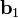и и 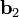. Этот перпендикуляр — вычисляемый в формуле (6) вектор ;

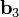5 — перемещение полученного 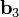в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (6).

На рисунке видно, что вектор 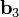ортогонален векторам 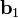и 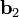, так как 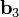является перпендикуляром, по которому 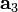проецируется на плоскость, образуемую векторам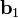и и .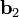

Таким образом, в процессе Грама — Шмидта для вычисления 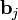выполняется проецирование 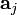ортогонально на гиперплоскость, формируемую векторами 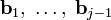. Вектор 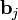затем вычисляется как разность между 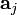и его проекцией. То есть 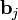— это перпендикуляр от конца 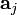к гиперплоскости, формируемой векторами 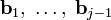. Поэтому 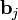ортогонален векторам, образующим эту гиперплоскость.

Геометрическая интерпретация — вариант 2

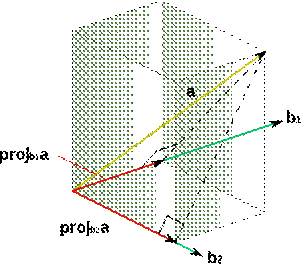
Рассмотрим проекции некоторого вектора 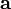на вектора 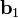и 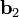как компоненты вектора 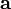в направлениях 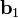и 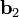(рис. 3)

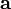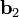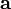Если удалить из компоненту в направлении , то станет ортогонален (рис. 4):

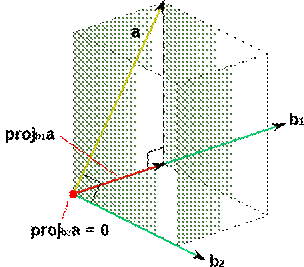
Если из удалить компоненты в направлениях и 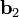, то станет ортогонален 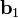и , и 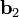(рис. 5):

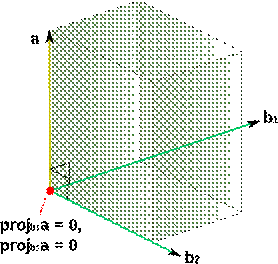
В формуле (2) из вектора 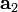удаляется компонента в направлении вектора 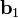. Получаемый вектор 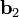не содержит компоненту в направлении 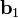и поэтому ортогонален вектору .

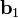В формуле (3) из вектора 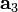удаляются компоненты в направлениях 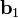и 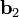(формуле 3 соответствует переход от рис. 3 к рис. 5; рис. 4 не соответствует формуле 3). Получаемый вектор 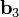ортогонален векторам 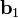и .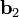

В формуле (4) из вектора 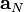удаляются компоненты в направлениях 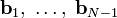. Получаемый вектор 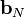ортогонален векторам .

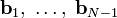Таким образом, по формулам (1) — (4) на основе векторов 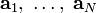получается набор ортогональных векторов .

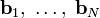Численная неустойчивость

При вычислении на ЭВМ по формулам (1) — (5) вектора 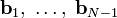часто не точно ортогональны из-за ошибок округления. Из-за потери ортогональности в процессе вычислений классический процесс Грама — Шмидта называют численно неустойчивым.