Уравнение (8) называется дифференциальным уравнением движения несвободной материальной точки в векторной форме.

2.2 Координатная форма

Проецируя векторное равенство (7) на координатные оси, получаем скалярные уравнения

= F_x

= F_у

= F_z

где

=

=

=

поэтому

(9)

Уравнения (9) называютсядифференциальными уравнениями свободной материальнойточки в координатной форме (декартовых координатах).

Очевидно, дифференциальные уравнения движения несвободной точкив декартовых координатах имеют вид

(10)

Уравнения (9) называютсядифференциальными уравнениями не свободной материальнойточки в координатной форме (декартовых координатах).

Существуют диф. уравнения первого, второго и др. порядков, зависят эти уравнения от старшей производной.

2.3 Естественная форма

Для записи диф. уравнений в естественной форме необходимо вспомнить кинематику.

Если траектория АВ точки М известна, то изображаем:

- траекторию движения точки,

- начало отсчета

- точку на траектории.

Затем изображаем естественную систему координат, для этого проводим касательную Направление касательной определяем ортом , затем изображаем главную нормаль и бинормаль, характеризуемые соответственно ортами

Плоскость образованную касательной и главной нормалью называют соприкасающейся плоскостью.

Теперь будем проецировать основное уравнение (1) на естественные оси.

Для свободной материальной точки

(11)

или

(12)

так как

Из последнего уравнения (11) видно, что траектория, описываемая точкой под действием силы 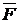, такова, что соприкасающаяся плоскость всегда содержит в себе эту силу.

Уравнения (11) называются дифференциальными уравнениями движениясвободной материальной точки вестественной форме.

По аналогии легко записать дифференциальные уравнения движениянесвободной точки в естественной форме

(13)

Замечание:

Реакция зависит от:

1) типа связей, наложенных на точку;

2) активной силы 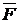, вызывающей движение точки: реакция может появиться только при наличии активной силы;

Движения самой точки.

Поэтому реакция 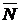заранее неизвестна.

Пример.

Рассмотрим движение груза M, подвешенного к нижнему концу гибкой нерастяжимой нити длиною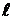

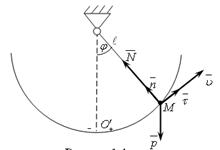
Уравнения (13) в данном случае имеют вид

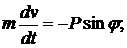
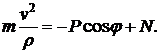
Откуда получаем

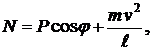
то есть реакция зависит от силы тяжести P, а также от положения точки на траектории, характеризуемого углом 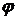, и её скорости 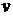в рассматриваемый момент времени.

Основные задачи динамики материальной точки.

В статике и кинематике мы решали две основные задачи. В динамике тоже мы будем решать две задачи.

Сначала будем рассматривать задачи для свободной материальной точке, а затем запишем замечания для несвободной материальной точки.

Первая основная (прямая) задача для свободной материальной точки.

Первая основная (прямая) задача.