Несовместные системы. Системы с общим решением. Частные решения

Продолжаем разбираться с системами линейных уравнений. До сих пор я рассматривал системы, которые имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом, методом Гаусса. Однако на практике широко распространены еще два случая:

– Система несовместна (не имеет решений);
– Система имеет бесконечно много решений.

Для этих систем применяют наиболее универсальный из всех способов решения – метод Гаусса. На самом деле, к ответу приведет и «школьный» способ, но в высшей математике принято использовать гауссовский метод последовательного исключения неизвестных. Те, кто не знаком с алгоритмом метода Гаусса, пожалуйста, сначала изучите урок метод Гаусса для чайников.

Сами элементарные преобразования матрицы – точно такие же, разница будет в концовке решения. Сначала рассмотрим пару примеров, когда система не имеет решений (несовместна).

Пример 1

Решить систему линейных уравнений

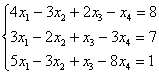
Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить.

Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

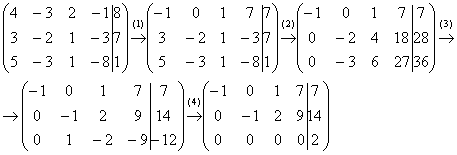
(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.

(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.

(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.

(4) К третьей строке прибавляем вторую строку.

Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: 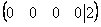. Ясно, что так быть не может. Действительно, перепишем полученную матрицу обратно в систему линейных уравнений:

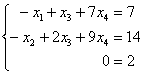
Если в результате элементарных преобразований получена строка вида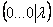 , где 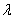– число, отличное от нуля, то система несовместна (не имеет решений).

Как записать концовку задания? Необходимо записать фразу «в результате элементарных преобразований получена строка вида 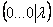, где 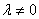» и дать ответ: система не имеет решений (несовместна).

Обратите внимание, что нет никакого обратного хода алгоритма Гаусса, решений нет и находить попросту нечего.

Пример 2

Решить систему линейных уравнений

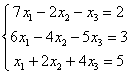
Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Снова напоминаю, что ваш ход решения может отличаться от моего хода решения, у алгоритма Гаусса нет сильной «жёсткости».

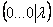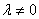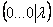Еще одна техническая особенность решения: элементарные преобразования можно прекращать сразу же, как только появилась строка вида , где . Рассмотрим условный пример: предположим, что после первого же преобразования получилась матрица . Матрица еще не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет никакой необходимости, так как появилась строка вида , где 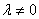. Следует сразу дать ответ, что система несовместна.

Когда система линейных уравнений не имеет решений – это почти подарок, ввиду того, что получается короткое решение, иногда буквально в 2-3 действия.

Но всё в этом мире уравновешено, и задача, в которой система имеет бесконечно много решений – как раз длиннее.

Пример 3

Решить систему линейных уравнений

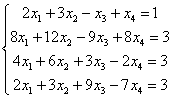
Тут 4 уравнений и 4 неизвестных, таким образом, система может иметь либо единственное решение, либо не иметь решений, либо иметь бесконечно много решений. Как бы там ни было, но метод Гаусса в любом случае приведет нас к ответу. В этом его и универсальность.

Начало опять стандартное. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

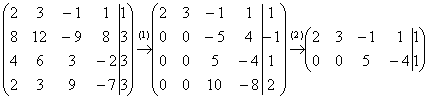
Вот и всё, а вы боялись.

(1) Обратите внимание, что все числа в первом столбце делятся на 2, поэтому на левой верхней ступеньке нас устраивает и двойка. Ко второй строке прибавляем первую строку, умноженную на –4. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –1.

Внимание! У многих может возникнуть соблазн из четвертой строки вычесть первую строку. Так делать можно, но не нужно, опыт показывает, что вероятность ошибки в вычислениях увеличивается в несколько раз. Только складываем: К четвертой строке прибавляем первую строку, умноженную на –1 – именно так!

(2) Последние три строки пропорциональны, две из них можно удалить.

Здесь опять нужно проявить повышенное внимание, а действительно ли строки пропорциональны? Для перестраховки (особенно, чайнику) не лишним будет вторую строку умножить на –1, а четвертую строку разделить на 2, получив в результате три одинаковые строки. И только после этого удалить две из них.

В результате элементарных преобразований расширенная матрица системы приведена к ступенчатому виду:

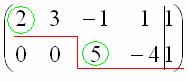
При оформлении задачи в тетради желательно для наглядности делать такие же пометки карандашом.

Перепишем соответствующую систему уравнений:

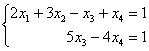
«Обычным» единственным решением системы здесь и не пахнет. Нехорошей строки 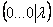тоже нет. Значит, это третий оставшийся случай – система имеет бесконечно много решений.

Бесконечное множество решений системы коротко записывают в виде так называемогообщего решения системы.

Общее решение системы найдем с помощью обратного хода метода Гаусса.

Сначала нужно определить, какие переменные у нас являются базисными, а какие переменные свободными. Не обязательно заморачиваться терминами линейной алгебры, достаточно запомнить, что вот существуют такие базисные переменные и свободные переменные.

Базисные переменные всегда «сидят» строго на ступеньках матрицы.
В данном примере базисными переменными являются 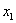и

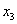
Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: 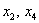– свободные переменные.

Теперь нужно все базисные переменные выразить только через свободные переменные.

Обратный ход алгоритма Гаусса традиционно работает снизу вверх.
Из второго уравнения системы выражаем базисную переменную :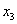

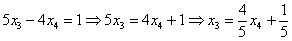
Теперь смотрим на первое уравнение: 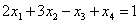. Сначала в него подставляем найденное выражение :

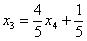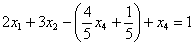
Осталось выразить базисную переменную 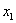через свободные переменные :

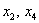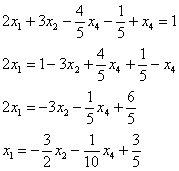
В итоге получилось то, что нужно – все базисные переменные ( 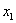и 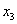) выражены только через свободные переменные :

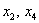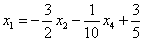
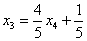
Собственно, общее решение готово:

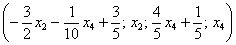
Как правильно записать общее решение?
Свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные 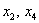следует записать на второй и четвертой позиции:
.

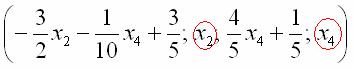Полученные же выражения для базисных переменных 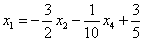и 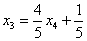, очевидно, нужно записать на первой и третьей позиции:

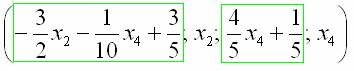
Из общего решения системы можно найти бесконечно много частных решений. Это очень просто.

Свободным переменным 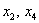можно придавать любые значения. Самыми популярными значениями являются нулевые значения, поскольку частное решение получается проще всего. Подставим 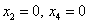в общее решение:

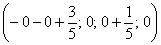
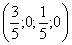– частное решение.

Другой сладкой парочкой являются единицы, подставим 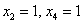в общее решение:

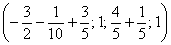
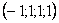– еще одно частное решение.

Легко заметить, что система уравнений имеет бесконечно много решений (так как свободным переменным мы можем придать любые значения)

Каждое частное решение должно удовлетворять каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение 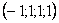и подставьте его в левую часть каждого уравнения исходной системы:

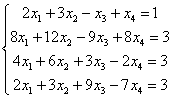
Всё должно сойтись. И с любым полученным вами частным решением – тоже всё должно сойтись.

Но, строго говоря, проверка частного решения иногда обманывает, т.е. какое-нибудь частное решение может удовлетворять каждому уравнению системы, а само общее решение на самом деле найдено неверно.

Поэтому более основательна и надёжна проверка общего решения. Как проверить полученное общее решение ?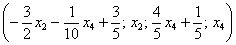

Это несложно, но довольно муторно. Нужно взять выражения базисных переменных, в данном случае 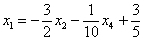и 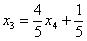, и подставить их в левую часть каждого уравнения системы.

В левую часть первого уравнения системы:

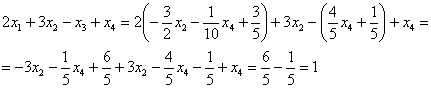
Получена правая часть исходного уравнения.

В левую часть второго уравнения системы:

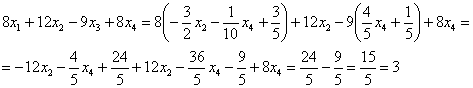
Получена правая часть исходного уравнения.

И далее – в левые части третьего и четвертого уравнение системы. Это дольше, но зато гарантирует стопроцентную правильность общего решения. Кроме того, в некоторых заданиях требуют проверку общего решения.

Пример 4

Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.

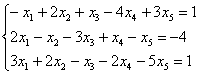
Это пример для самостоятельного решения. Здесь, кстати, снова количество уравнений меньше, чем количество неизвестных, а значит, сразу понятно, что система будет либо несовместной, либо с бесконечным множеством решений. Что важно в самом процессе решения? Внимание, и еще раз внимание. Полное решение и ответ в конце урока.

И еще пара примеров для закрепления материала

Пример 5

Решить систему линейных уравнений. Если система имеет бесконечно много решений, найти два частных решения и сделать проверку общего решения

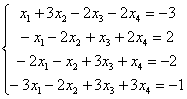
Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

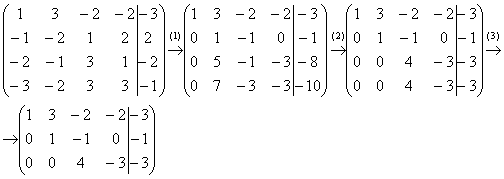
(1) Ко второй строке прибавляем первую строку. К третьей строке прибавляем первую строку, умноженную на 2. К четвертой строке прибавляем первую строку, умноженную на 3.
(2) К третьей строке прибавляем вторую строку, умноженную на –5. К четвертой строке прибавляем вторую строку, умноженную на –7.
(3) Третья и четвертая строки одинаковы, одну из них удаляем.

Вот такая красота:

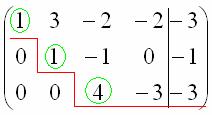
Базисные переменные сидят на ступеньках, поэтому 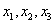– базисные переменные.
Свободная переменная, которой не досталось ступеньки здесь всего одна: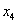

Обратный ход:
Выразим базисные переменные через свободную переменную:
Из третьего уравнения:

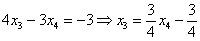
Рассмотрим второе уравнение 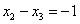и подставим в него найденное выражение :

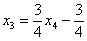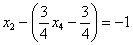
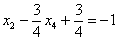
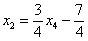
Рассмотрим первое уравнение 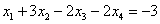и подставим в него найденные выражения 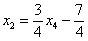и :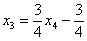

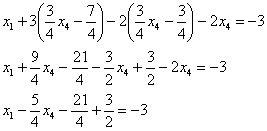
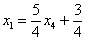
Да, всё-таки удобен калькулятор, который считает обыкновенные дроби.

Таким образом, общее решение:

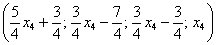
Еще раз, как оно получилось? Свободная переменная 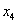одиноко сидит на своём законном четвертом месте. Полученные выражения для базисных переменных 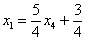, , 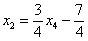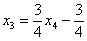тоже заняли свои порядковые места.

Сразу выполним проверку общего решения. Работа для негров, но она у меня уже выполнена, поэтому ловите =)

Подставляем трех богатырей 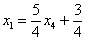, , 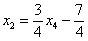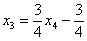в левую часть каждого уравнения системы:

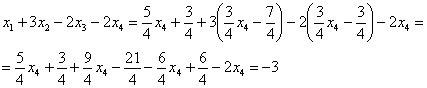
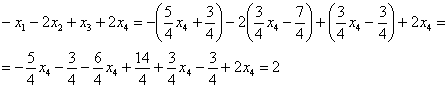
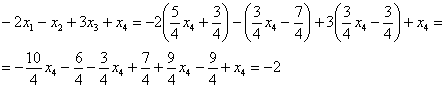
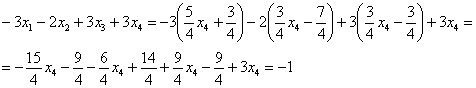
Получены соответствующие правые части уравнений, таким образом, общее решение найдено верно.

Теперь из найденного общего решения 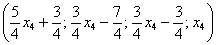получим два частных решения. Шеф-поваром здесь выступает единственная свободная переменная 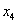. Ломать голову не нужно.

Пусть 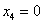, тогда 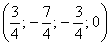– частное решение.
Пусть 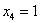, тогда 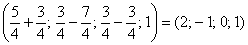– еще одно частное решение.

Ответ: Общее решение: 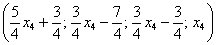, частные решения: , .

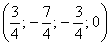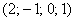Зря я тут вспомнил про негров, потому-что в голову полезли всякие садистские мотивы, и вспомнилась карикатура, где куклуксклановцы в своих белых балахонах бегут по футбольному полю за чернокожим футболистом. Сижу, тихо улыбаюсь. Знаете, как отвлекает….

Много математики вредно, поэтому похожий заключительный пример для самостоятельного решения.

Пример 6

Найти общее решение системы линейных уравнений.

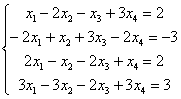
Проверка общего решения у меня уже сделана, ответу можно доверять. Ваш ход решения может отличаться от моего хода решения, главное, чтобы совпали общие решения.

Наверное, многие заметили неприятный момент в решениях: очень часто при обратном ходе метода Гаусса нам пришлось возиться с обыкновенными дробями. На практике это действительно так, случаи, когда дробей нет – встречаются значительно реже. Будьте готовы морально, и, самое главное, технически.

Остановлюсь на некоторых особенностях решения, которые не встретились в прорешанных примерах.

В общее решение системы иногда может входить константа (или константы), например: 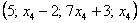. Здесь одна из базисных переменных равна постоянному числу: 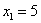. В этом нет ничего экзотического, так бывает. Очевидно, что в данном случае любое частное решение будет содержать пятерку на первой позиции.

Редко, но встречаются системы, в которых количество уравнений больше количества переменных. Метод Гаусса работает в самых суровых условиях, следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и, как ни странно, может иметь единственное решение.

И, конечно, повторюсь в своем совете – чтобы комфортно себя чувствовать при решении системы методом Гаусса, следует набить руку и прорешать хотя бы десяток систем.

Желаю успехов!

Решения и ответы:

Пример 2:Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

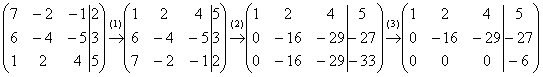
Выполненные элементарные преобразования:
(1) Первую и третью строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –6. К третьей строке прибавили первую строку, умноженную на –7.
(3) К третьей строке прибавили вторую строку, умноженную на –1.
В результате элементарных преобразований получена строка вида 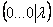, где , значит, система несовместна.
Ответ:решений нет.

Пример 4:Решение:Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

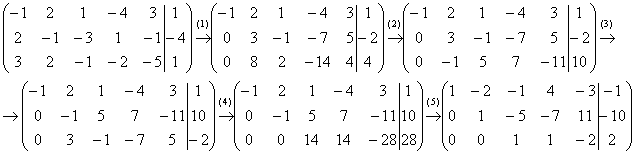
Выполненные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на 2. К третьей строке прибавили первую строку, умноженную на 3.

Для второй ступеньке нет единицы, и преобразование (2) направлено на её получение.

(2) К третьей строке прибавили вторую строку, умноженную на –3.
(3) Вторую с третью строки поменяли местами (переставили полученную –1 на вторую ступеньку)
(4) К третьей строке прибавили вторую строку, умноженную на 3.
(5)У первых двух строк сменили знак (умножили на –1), третью строку разделили на 14.

Обратный ход.
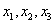– базисные переменные (те, которые на ступеньках), 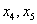– свободные переменные (те, кому не досталось ступеньки).

Выразим базисные переменные через свободные переменные:
Из третьего уравнения: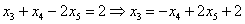

Рассмотрим второе уравнение: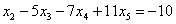
Подставим в него найденное выражение :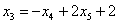

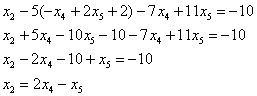
Рассмотрим первое уравнение: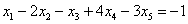
Подставим в него найденные выражения: , :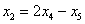

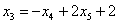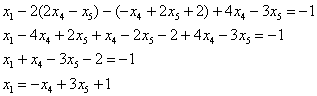
Общее решение: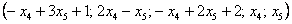

Найдем два частных решения
Если 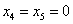, то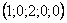
Если 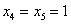, то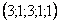

Ответ:Общее решение: 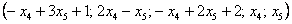, частные решения: , .

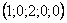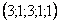Проверка: подставим найденное решение (выражения базисных переменных 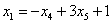, 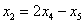и 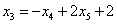) в левую часть каждого уравнения системы:

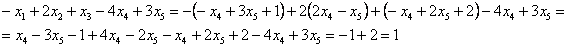
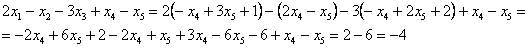
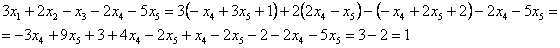
Получены соответствующие правые части, таким образом, общее решение найдено верно.

Пример 6:Решение:Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

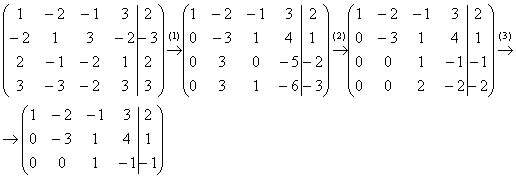
(1) Ко второй строке прибавляем первую строку, умноженную на 2. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –3.
(2) К третьей строке прибавляем вторую строку. К четвертой строке прибавляем вторую строку.
(3) Третья и четвертая строки пропорциональны, одну из них удаляем.

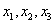– базисные переменные, 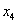– свободная переменная. Выразим базисные переменные через свободную переменную:

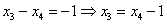
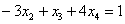
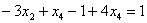
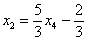
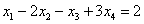
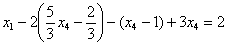
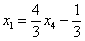
Ответ:Общее решение: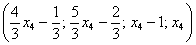

Комплексные числа

Не занимайтесь комплексными числами после комплексного обеда

На данном уроке мы познакомимся с понятием комплексного числа, рассмотрим алгебраическую, тригонометрическую и показательную форму комплексного числа. А также научимся выполнять действия с комплексными числами: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Не беспокойтесь, я вас напугал, я вас и рассмешу. Для освоения комплексных чисел не требуется каких-то специальных знаний из курса высшей математики, и материал доступен даже школьнику. Достаточно уметь выполнять основные алгебраические действия с «обычными» числа, и немного рубить в тригонометрии, впрочем, если что забылось, я напомню.

Урок состоит из следующих параграфов:
1) Понятие комплексного числа.
2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел.
3) Тригонометрическая и показательная форма комплексного числа.
4) Возведение комплексных чисел в степень.
5) Извлечение корней из комплексных чисел.

На любой вкус и цвет – кому, что интересно. А комплексные числа действительно становятся наиболее интересной темой, после того, как студенты знакомятся с другими разделами высшей алгебры =). Если Вы являетесь чайником, или только-только приступили к изучению комплексных чисел, то параграфы лучше прочитать по порядку, без «перескоков».

Сначала вспомним «обычные» школьные числа. В математике они называются множеством действительных чисел и обозначаются буквой 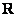(в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа сидят на знакомой числовой прямой:

Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой обязательно соответствует некоторое действительное число.

Понятие комплексного числа

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Если хотите, комплексное число – это двумерное число. И курить бессмысленно. … Так, кто тут улыбается? Видимо, действительно не помогло.

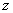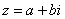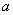Комплексным числом называется число вида , где и 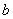– действительные числа, 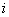– так называемая мнимая единица. Число 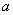называется действительной частью ( 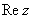)комплексного числа 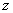, число 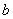называется мнимой частью ( 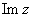) комплексного числа .

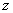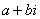– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: 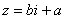или переставить мнимую единицу: 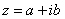– от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: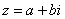

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:

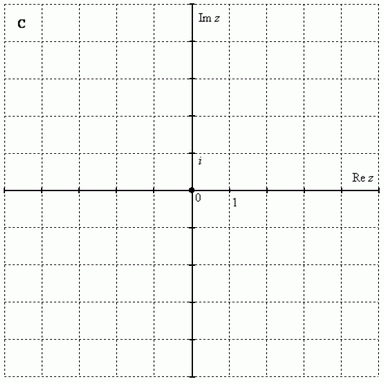
Как упоминалось выше, буквой 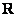принято обозначать множество действительных чисел.Множествожекомплексных чиселпринято обозначать «жирной» или утолщенной буквой 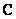. Поэтому на чертеже следует поставить букву 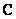, обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей:
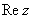– действительная ось
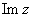– мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать размерность, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу 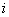по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .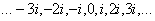

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:
, ,
, ,
, , ,

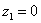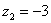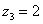
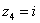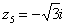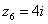
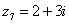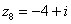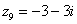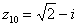
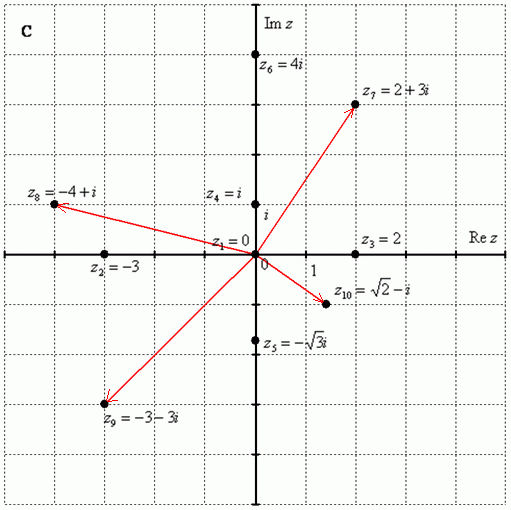
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Рассмотрим следующие комплексные числа: 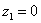, , 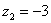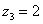. Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось 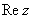обозначает в точности множество действительных чисел 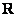, то есть на оси 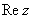сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел 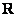является подмножеством множества комплексных чисел .

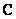Числа 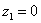, , 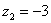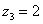– это комплексные числа с нулевой мнимой частью.

Числа 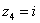, , 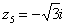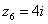– это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

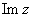В числах 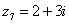, , 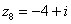, 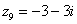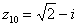и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому-что они сливаются с осями.

Алгебраическая форма комплексного числа.
Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились, 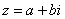– это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,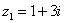

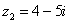
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

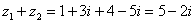
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса: 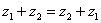– от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел 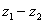и 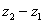, если ,

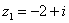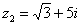
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

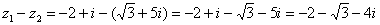
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: 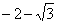. Для наглядности ответ можно переписать так: .

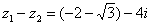Рассчитаем вторую разность:

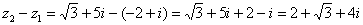
Здесь действительная часть тоже составная: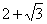

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: 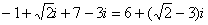. Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

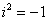
Пример 3

Найти произведение комплексных чисел ,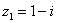

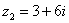
Очевидно, что произведение следует записать так:

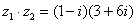
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что 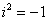и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

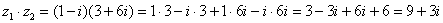
Надеюсь, всем было понятно, что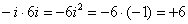

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .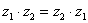

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа 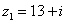, 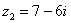. Найти частное .

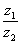Составим частное:

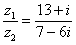
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу 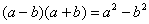и смотрим на наш знаменатель: 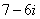. В знаменателе уже есть 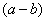, поэтому сопряженным выражением в данном случае является