Основная цель математической логики – обеспечить систему формальных обозначений для рассуждений, встречающихся не только в математике, но и в повседневной жизни.

Решим следующую задачу, используя законы сложения и умножения высказываний.

Задача 4. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники были на синем «Бьюике»; Джонс сказал, что это был чёрный «Крайслер», а Смит утверждал, что это был «Форд Мустанг» и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо её цвет. Какого цвета был автомобиль и какой марки?

Решение.

1) Перечислим все имеющиеся высказывания:

Aº{машина синего цвета} – 1-е показание Брауна,

Bº{машина марки «Бьюик»} – 2-е показание Брауна,

Cº{машина чёрного цвета} – 1-е показание Джонса,

Dº{машина марки «Крайслер»} – 2-е показание Джонса,

Eºмашина марки «Форд Мустанг»} – 1-е показание Смита,

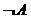– 2-е показание Смита.

2) По условию задачи каждый из подозреваемых сказал правду или только про марку машины, или про её цвет.

Т.к. Браун дал показания А, В, то А или В – правда, что в записи математической логики будет выглядеть: «истина».

Джонс дал показания C, D, т.е. С или D – правда, что есть «истина».

Смит дал показания E, 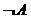, т.е. Е или 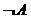– правда, что есть «истина».

3) Следствие имеет показания Брауна и Джонса и Смита, т.е.

и и ,

что в записи математической логики есть

«истина»,

т.к. истинно каждое из высказываний , , .

4) Имеем: «истина».

Перепишем последнее выражение, учитывая, что  является логической суммой, а  есть логическое произведение:

«истина».

Раскроем скобки:

«истина».

5) Проанализируем каждое из слагаемых полученного выражения:

«ложь», т.к. в этом выражении одновременно утверждается, что машина и синего и не синего цвета;

«ложь», т.к. в этом выражении одновременно утверждается, что машина и синего и чёрного цвета;

«ложь», т.к. в этом выражении одновременно утверждается, что машина и синего и не синего цвета;

«ложь», т.к. в этом выражении одновременно утверждается, что машина «Крайслер» и машина «Форд Мустанг» ;

машина марки «Бьюик» и машина чёрного цвета и машина не синего цвета}

– в этом выражении внутренних противоречий нет, но мы пока что не знаем, истинно оно или ложно;

«ложь», т.к. в этом выражении одновременно утверждается, что машина «Бьюик» и машина «Форд Мустанг» ;

«ложь», т.к. в этом выражении одновременно утверждается, что машина «Бьюик» и машина «Крайслер» ;

«ложь», т.к. в этом выражении одновременно утверждается, что машина «Бьюик» и машина «Крайслер» .

6) Получили:

«ложь»  «ложь»  «ложь»  «ложь»   «ложь»  «ложь»  «ложь» =  «ложь» = = = «истина», т.е. преступники скрылись на чёрном «Бьюике».

Задачи для самостоятельного решения

Задача 1.

Докажите формулу: AB =AB.

Задача 2.

На вопрос, кто из трёх студентов изучал логику, был получен правильный ответ: если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй. Кто из студентов изучал логику?

Задача 3.

«Вернувшись домой, комиссар Мегрэ позвонил в полицейский отдел на набережную Орфевр.

- Говорит Мегрэ. Есть новости?

- Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжёт. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи. Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжёт. Затем звонила …

- Всё. Спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжёт. Теперь он знал всё».

Какой вывод сделал комиссар Мегрэ?

Указания.

1. Рассмотрите следующие высказывания:

A  {Франсуа был пьян},

B  {Этьен убийца},

C  {Франсуа лжёт},

D  {убийство произошло после полуночи}.

2. Запишите, используя логические операции, высказывания инспекторов Торранса, Жуссье и Люка. Составьте произведение этих трёх высказываний и упростите его.

Задача 4.

Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. На следствии каждый из них сделал два заявления.

Браун. Я не делал этого.

Смит сделал это.

Джонс. Смит не виновен.

Браун сделал это.

Смит. Я не делал этого.

Джонс не делал этого.

Суд установил, что один из них дважды солгал, другой – дважды сказал правду, третий – один раз солгал, один раз сказал правду.

Кто совершил преступление?

Числа

Наиболее общие закономерности и законы экономических явлений выясняются путем качественного анализа, но конкретное выражение их возможно лишь с помощью меры и числа.

Число - важнейшее математическое понятие, меняющееся на протяжении веков. Первые представления о числе возникли из счета людей, животных, плодов, различных изделий и пр. Результатом являются натуральные числа: 1, 2, 3, 4…

При счете отдельных предметов единица есть наименьшее число, и делить ее на доли не нужно, а иногда и нельзя, однако уже при грубых измерениях величин приходится делить 1 на доли.

Исторически первым расширением понятия числа является присоединение к натуральному числу дробных чисел. Дробью называется часть (доля) единицы или несколько равных ее частей.

Дроби обозначаются, как : , где m и n - целые числа;

- это сокращение дроби; а - это расширение дроби.

Дроби со знаменателем 10 - это десятичные дроби: .

Среди десятичных дробей особое место занимают периодические дроби: 0,2525…=0,(25)= - чистая периодическая дробь, 1,2555…=1,2(5)= - смешанная периодическая дробь.

Дальнейшее расширение понятия числа вызвано уже развитием самой математики (алгебры).

Декарт в 17 веке вводит понятие отрицательного числа. Числа целые (положительные и отрицательные), дробные (положительные и отрицательные) и нуль получили название рациональных чисел. Всякое рациональное число может быть записано в виде дроби конечной и периодической. Для изучения непрерывно изменяющихся переменных величин оказалось необходимым новое расширение понятия числа - введение действительных (вещественных) чисел - присоединением к рациональным числам иррациональных: иррациональные числа - это бесконечные десятичные непериодические дроби.

Иррациональные числа появились при измерении несоизмеримых отрезков (сторона и диагональ квадрата). В алгебре иррациональные числа появились при извлечении корней . Примером трансцендентного, или иррационального числа являются числа π, е.

Все действительные числа можно изобразить на числовой оси. Числовая ось(числовая прямая) это:

а) горизонтальная прямая линия с выбранным на ней направлением;

б) на оси задано начало отсчета – нулевая точка 0;

в) на оси задана единица масштаба.

Х

-2 -1 1 2 3