Особенности анализа цепей с НЭ

Нелинейные цепи.

Основные понятия.

Нелинейные электрические цепи – цепи, содержащие хотя бы один нелинейный элемент, т.е. элемент, параметры которого (R, L или C) зависят от значений или от направления тока и напряжения этого элемента цепи.

В зависимости от способности рассеивать электрическую энергию в виде тепла (необходимо преобразовывать в другие виды энергии) или накапливать магнитную или электрическую энергию (или накапливать в виде энергии магнитного или электрического полей) различают:

РНЭ – резистивный нелинейный элемент;

ИНЭ – индуктивный нелинейный элемент;

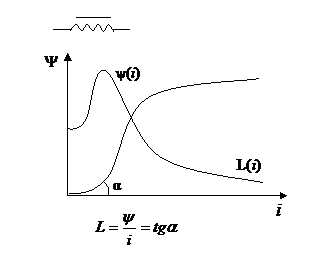
ЕНЭ – емкостный нелинейный элемент.

РНЭ, ИНЭ, ЕНЭ – нелинейные накопители энергии.

Характеристиками этих элементов, получаемыми экспериментальными и задаваемыми графиками, таблицами или приближенными аналитическими выражениями являются:

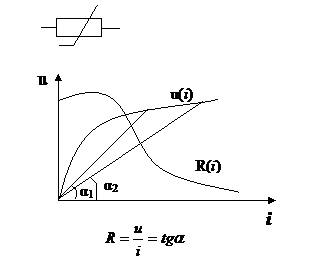
-вольтамперная характеристика (ВАХ) РНЭ – u (i)

-вебер-амперная характеристика ИНЭ – Y (i) – магнитная характеристика нелинейных индуктивных элементов

-кулон-вольтная характеристика ЕНЭ – q (u) электрическая характеристика емкостных нелинейных элементов.

Причиной нелинейности характеристик элементов является нелинейность параметров этих элементов – R, L, C.

Параметры этих нелинейных элементов (НЭ) – сопротивление, индуктивность, емкость – зависят от величин и направлений тока и напряжения этих элементов. Причиной этого является зависимость:

- удельной проводимости g (удельного сопротивления r) от режима цепи

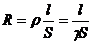
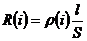или

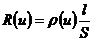
- магнитной проницаемости среды m, в которой замыкаются силовые линии магнитного поля от тока, возбудившего это поле (от напряженности поля)

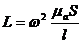
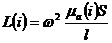
- диэлектрической проницаемости вещества, заполняющего пространство между обкладками конденсатора, от напряжения между обкладками (от напряжения электрического поля)

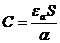
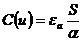
Для оценки характера изменения НЭ вводят понятие статического и дифференциального сопротивлений.

Статическое сопротивление Rст характеризует поведение НРЭ при неизменном режиме. В рассматриваемой точке ВАХ численно равно тангенсу угла наклона между осью ординат (осью токов) и прямой, соединяющей начало координат и рассматриваемую точку ВАХ, умноженного на масштаб

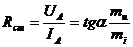
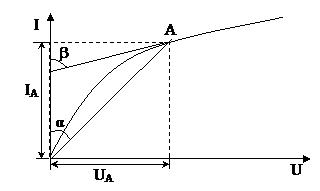
Дифференцированное сопротивление Rдиф определяет крутизну ВАХ в рассматриваемой точке и характеризует поведение НРЭ при малых отклонениях от режима в рассматриваемой точке ВАХ. Rдиф численно равно тангенсу угла наклона между осью ординат и касательной к ВАХ в рассматриваемой точке, умноженного на масштаб.

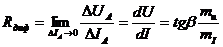
а) При последовательном соединении нескольких НРЭ Rдиф результирующей характеристики при каком-то токе равно сумме Rдиф этих НРЭ при этом же токе (т.к. производная суммы равна сумме производных)

б) Если ВАХ НРЭ имеет падающий участок, то Rдиф на этом участке отрицательно.

Примеры нелинейных элементов и их характеристик

Неуправляемые

РНЭ – лампа накаливания (1) – с ростом температуры сопротивление растет, характеристика симметричная.

- (2) тиритовые сопротивления (из керамического материала – тирита) – тиритовые разрушаются от высокого напряжения;

- терферисторы – для компенсации изменения сопротивления приборов от температуры;

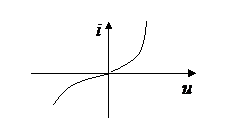
- (3) бареттер – стальная проволока в водороде (80мм рт ст) – для стабилизации тока;

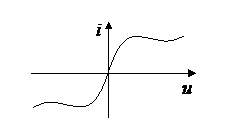
- (4) диод (несимметричная характеристика), стабилитрон

Управляемые

- транзистор – характеризуется семейством характеристик;

- ИНЭ – дроссель – катушка индуктивности с обмоткой, намотанной на замкнутый сердечник из ферромагнитного материала;

- ЕНЭ – конденсатор, между обкладками которого сегнетодиэлектрик (впервые эти свойства обнаружены у сегнетовой соли).

Графический метод

Графический метод основан на графических построениях с использованием ВАХ НЭ, представленных в виде графика или таблицы, а также связанные с этими построениями расчетами с использованием законов Кирхгофа.

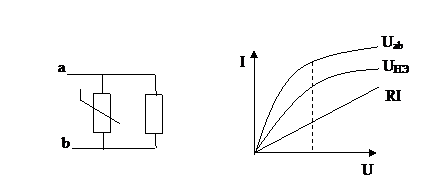
1. ВАХ двухполюсника

Важное место при этом занимает построение ВАХ пассивных и активных двухполюсников, содержащих линейные и нелинейные элементы.

ВАХ двухполюсника строят в соответствии с уравнениями, составленными по законам Кирхгофа, путем графического сложения ВАХ элементов, входящих в двухполюсник. Это графический аналог метода эквивалентных преобразований.

2. Схемы со смешанным соединением.

Зная ВАХ активных и пассивных двухполюсников любую цепь можно свести к одноконтурной схеме или схеме с двумя узлами.

Для этого записав уравнение на основании I закона Кирхгофа для схемы с двумя узлами и II закона Кирхгофа для одноконтурной цепи решить его графическим путем нахождения точки пересечения эквивалентных ВАХ, соответствующих левой и правой частям уравнения.

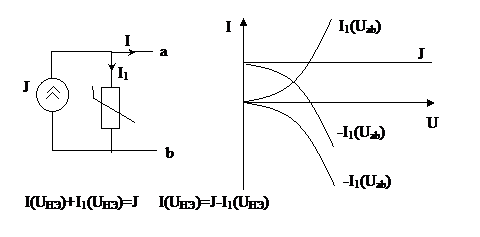
3. Сложноразветвленные

Метод эквивалентного генератора эффективен при разветвленной цепи любой сложности, содержащей один НРЭ. В этом случае линейную часть замещают эквивалентным генератором, а затем определяют режим в НЭ путем графического решения уравнения составленного по II закону Кирхгофу.

Алгоритм

1) Рассматривать схему как линейный активный четырехполюсник с подключениями к его зажимам НЭ.

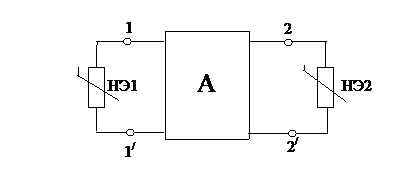
2) Отключить НЭ и рассчитать напряжения хх на зажимах четырехполюсника одним из известных методов (МУН).

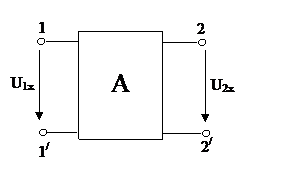
3) В теории цепей доказывается, что если две ветви одновременно ввести две э.д.с., равные и противоположно направленные напряжениям холостого хода на этих ветвях (E1 = U1x; E2 = U2x), то токи в этих ветвях найдутся из схемы, т.е. заданный активный четырехполюсник заменяется пассивным и двумя э.д.с., равных и противоположно направленными напряжениями хх на зажимах этого четырехполюсника.

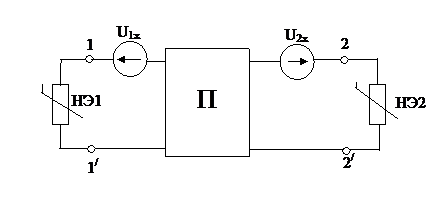
4) Заменив пассивный четырехполюсник Т-образной схемой замещения, получаем нелинейную цепь с двумя узлами, решение которой можно осуществить:

а) графическим методом;

б) методом аналитической аппроксимации:

- составление уравнений, подстановка аппроксимирующей функции, решение трансцендентного или алгебраического уравнения;

- составление уравнений, решение численным (итерационным) методом.

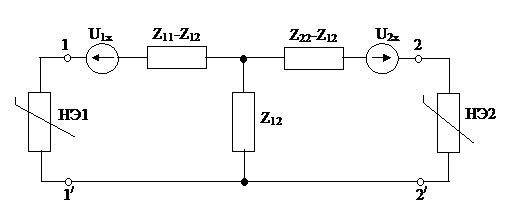
Аналитический метод

1. Метод аналитической аппроксимации.

ВАХ НРЭ заменяют аналитической функцией, приближенно описывающей ВАХ (полином, тригонометрическое выражение и т.д.). Затем применяют один из известных методов расчета из теории линейных цепей. В результате получают алгебраические или трансцендентные уравнения, которые решают аналитически относительно искомой величины.

2. Методы линеаризации (в малом).

При малых отклонениях режима от исходного (от т.а.), небольшой участок ВАХ приближенно можно заменить отрезком прямой, касательной к характеристике в т.а. При этом ВАХ заменяется на ломаную, которую можно представить как э.д.с. и линейное сопротивление, равное дифференциальному.

3. Кусочно-линейная аппроксимация.

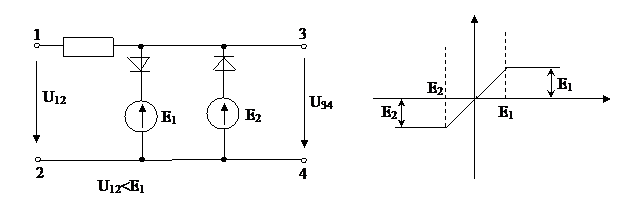
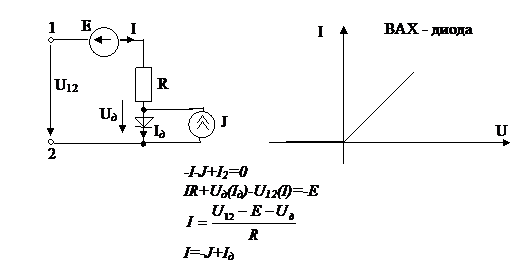
- Источник тока шунтирован диодом;

- напряжение на диоде U_д;

- диод открыт постоянно.

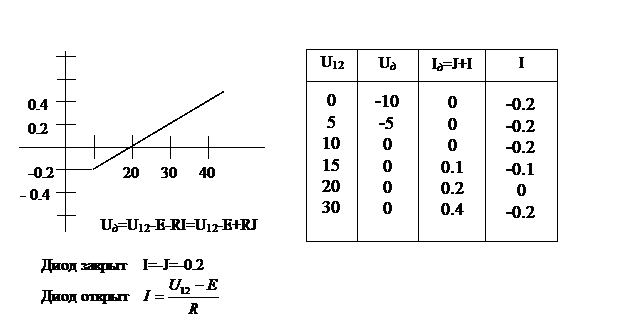
4. Численные методы (итерации).

Расчет ведется в табличной форме.

Задаемся Uab Þ U1(I1)= Uab-E1Þ I1(по ВАХ) Þ

U2(I2)= Uab-E2Þ I2(по ВАХ) Þ åI

U3(I3)= Uab-E3Þ I3(по ВАХ) Þ

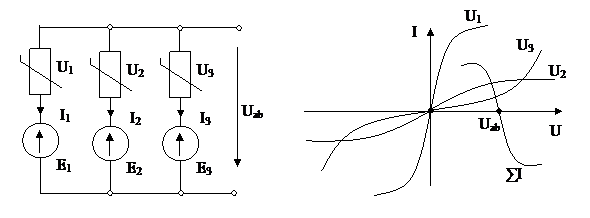
Задаваясь другими значениями Uab продолжают эту операцию до тех пор, пока åI не изменит знак. Затем в большом масштабе строят участок åI=ƒ(Uab) вблизи нуля. Искомое значение Uab соответствует åI=0

Задача:

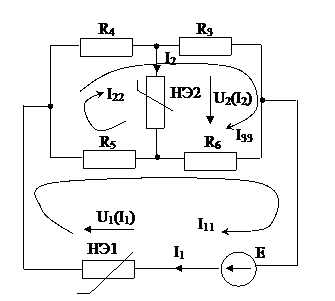
Свести к уравнениям с неизвестными токами через НЭ. Для этого:

1) 2-ое уравнение с участием нелинейных элементов (I11, I22);

2) 1-ое уравнение линейное (I33);

3) Выразить с помощью линейного уравнения через I33 I1= I11 и I2= I22 и подставить в уравнения.

Решение

1. Метод контурных токов. Контурные токи выбрать так, чтобы хотя бы часть из них являлась искомыми токами через нелинейные элементы.

2. По второму закону Кирхгофа.

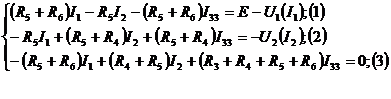
3. Одно из уравнений (3) линейное и полученное из него выражение для I33 подставляется в равнения (1) и (2)

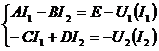
4. Итерация.

- Задаемся I1 и I2;

- определяем U₁ и U₂ по ВАХ НЭ₁ и НЭ₂;

- получаем первое приближение I₁¹ и I₂¹ из уравнений;

- определяем U₁¹ и U₂¹ по ВАХ НЭ₁ и НЭ₂;

- получаем второе приближение I₁² и I₂².

Окончание ;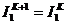

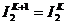
Основные понятия.

Особенность НЦ переменного тока – зависимость параметров нелинейного элемента от частоты приложенного напряжения и протекающего тока (в дополнение к зависимости от их величины и направления)

Пример:

· кривая перемагничивания дросселя;

· поверхностный эффект в резистивных цепях.

Однако, в цепях переменного тока, в отличие от цепей постоянного тока, нелинейный элемент может быть описан тремя видами характеристик:

· вольт – амперные характеристики для мгновенных значений,

· вебер – амперные характеристики по первым гармоникам,

· кулон – вольтные характеристики для действующих значений.

Если воздействующее на нелинейный элемент напряжение (ток) содержит постоянную составляющую, то вольт – амперные, вебер- амперные или кулон – вольтные характеристики изображают семействами кривых, на которых постоянная составляющая воздействующей величины является параметром.

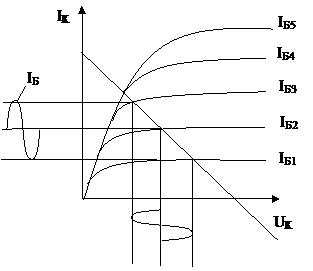
Характеристики для мгновенных значений связывают мгновенные значения основных определяющих величин – U и i, Ψ и i, q и U.

ВАХ по первым гармоникам – связь между амплитудными (действующими) значениями первых гармоник тока и напряжение на нелинейном элементе.

ВАХ для действующих значений – зависимость между действующими значениями тока и напряжения на нелинейном элементе.

ВАХ по первым гармоникам и действующим значениям получают графическим или аналитическим путем из характеристик для мгновенных значений или снимают опытным путем, экспериментально.

Графический метод

Графоаналитический метод основан на использовании характеристик нелинейных элементов для мгновенных значений и уравнений Кирхгофа.

1. Записывают уравнения Кирхгофа для мгновенных значений.

2. Пользуясь вольтамперной характеристикой (вебер-амперной, кулон-вольтной) НЭ строят графические зависимости u(t) и i(t),т.е. графические зависимости изменения искомых величин во времени.

Рассмотрим практически НЭ – дроссель (катушка с ферромагнитным сердечником), питаемой от сети синусоидального напряжения.

Получим для облегчения анализа, что:

-сопротивление обмотки равно нулю;

-поток рассеяния равен нулю.

Согласно II закону Кирхгофа

С=0, т.к. напряжение синусоидальное

Выводы:

1. Магнитный поток в сердечнике полностью определяется напряжением на обмотке и не зависит от параметров магнитной цепи.

2. При синусоидальном напряжении питания поток в сердечники также синусоидален.

3. Поток отстает от приложенного напряжения на .

4. Амплитуда потока в сердечнике дросселя зависит только от величины приложенного напряжения (при ¦_сети=const и W _{дросселя} =const)

Выясним теперь характер изменения тока. Воспользуемся вебер-амперной характеристикой.

В результате графических построений получаем кривую тока i.

Выводы:

1. Ток несинусоидален. Причем вследствие симметричности кривой тока относительно оси абсцисс при различении будут отсутствовать четные гармоники (присутствуют 3-я, 5-я, 7-я). Кривая тока i имеет заостренную форму.

2. Ток достигает max одновременно с потоком. Причем, чем больше насыщен сердечник, тем больше max тока.

3. Ток отстает от напряжения на , где d - угол потерь магнитных, обусловлен явлением гистерезиса и пропорциональный потерям энергии в единице объема сердечника за 1 цикл перемагничивания.

Пример.

Выпрямление, усиление, ограничение.

Односторонний ограничитель напряжения.

Ограничитель тока.

Достоинства метода: простота, наглядность, легкость учета особенностей ВАХ.

Недостаток: графическое построение не позволяет проводить анализ в общем виде, а дает решение только для частных значений параметров.

Если , то кривая потока отлична от синусоиды и имеет упрощенную форму. Кривая же напряжения (э.д.с. ) при этом имеет весьма заостренную форму. Построение кривой потока по вебер-амперной характеристике и заданной кривой тока стоится графически. Кривую u(t) получают дифференцированием кривой ψ(t).

Полученные периодические несинусоидальные кривые изменения искомых величин могут быть разложены в ряд Фурье (аналитически или графически), что позволит определить их действующее значение.

Пренебрежение высшими гармониками и расчет действующего значения первой гармоники приводит к погрешности в несколько процентов.

Пример. Ток в цепи

I_3m=0,4I_1m

Т.е. наличие 3-й гармоники, составляет 40% от 1-ой, увеличивает действующее значение на 7,5%.

Аналитический метод

Метод аппроксимации основан на решении уравнений состояния цепей при приближенной замене (аппроксимации) характеристик нелинейных элементов в пределах рабочего участка аналитическими выражениями.

Метод линеаризации. Аппроксимация осуществляется прямой линией.

Метод кусочно-линейной аппроксимации. Аппроксимация отрезками прямой линии.

Численные методы. Метод итерации, Ньютона.

Аппроксимация сплайнами.

Графический метод

ВАХ для действующих значений НЭ задана в виде графика.

Расчет графическим методом ведется аналогично графическому расчету нелинейных цепей постоянного тока (расчету нелинейных цепей с инерционными элементами).

Если цепь содержит активные и реактивные элементы, то токи и напряжения складываются в квадратуре (см. явление феррорезонанса).

Аналитический метод

В этом случае ВАХ аппроксимируется аналитической функцией кусочно-линейной или линейной аппроксимацией, сплайнами.

Расчет ведется аналогично цепям постоянного тока с учетом квадратуры соотношений токов и напряжений.

В тех случаях, когда вопрос о форме несинусоидальных кривых токов и напряжений не представляет особого интереса (с точки зрения эксплуатации, возможности повреждения, опасных перенапряжений и т.д.) можно воспользоваться приближенным аналитическим методом, основанным на замене действительных несинусоидальных кривых тока и напряжения эквивалентными синусоидами. Основанный на такой замене метод анализа – метод эквивалентных синусоид.

Смысл введение этого метода заключается в возможности записи уравнений в комплексной форме, а также в построении векторных диаграмм, хотя комплексные сопротивления остаются зависимыми от тока, а, следовательно, алгебраические уравнения, записанные в комплексной форме, остаются нелинейными.

Выбор эквивалентных синусоид тока и напряжения, т.е. их амплитуд и начальных фаз, может быть осуществлен тем или иным способом. Интересуясь энергетической стороной процесса, этот выбор целесообразно осуществить так, чтобы активная мощность в цепи оставалась без изменения.

В электрических проводниках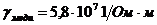

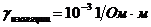
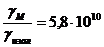
В магнитных цепях .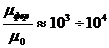

Поэтому возникает поток рассеяния! Это линии с распределенными параметрами.

Пример 1.

Ток в цепи содержит:

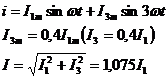
т.е. наличие 3-й гармоники, составляющей 40% от 1-й, увеличивает действующее значение несинусоидального тока по сравнению с действующим значением 1-й гармоники на 7,5%.

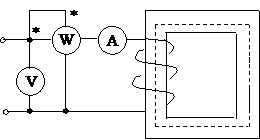
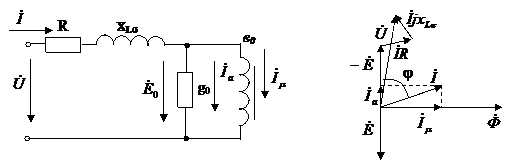
Пример 2.

u – синусоидальное

i – несинусоидальный.

Эквивалентной синусоидой должна быть первая гармоника тока, т.к.

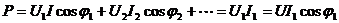
Пример 3.

u – синусоидальное

i – несинусоидальный.

Чтобы активная мощность цепи осталась неизменной p=I²r необходимо, чтобы действующее значении тока осталось неизменным, т.е. заменить несинусоидальный ток синусоидой, эквивалентной ему по действующему значению.

Нелинейные цепи.

Основные понятия.

Нелинейные электрические цепи – цепи, содержащие хотя бы один нелинейный элемент, т.е. элемент, параметры которого (R, L или C) зависят от значений или от направления тока и напряжения этого элемента цепи.

В зависимости от способности рассеивать электрическую энергию в виде тепла (необходимо преобразовывать в другие виды энергии) или накапливать магнитную или электрическую энергию (или накапливать в виде энергии магнитного или электрического полей) различают:

РНЭ – резистивный нелинейный элемент;

ИНЭ – индуктивный нелинейный элемент;

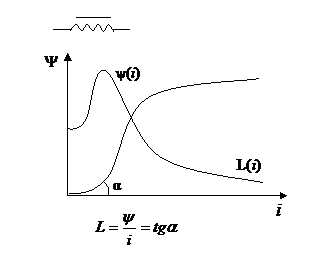
ЕНЭ – емкостный нелинейный элемент.

РНЭ, ИНЭ, ЕНЭ – нелинейные накопители энергии.

Характеристиками этих элементов, получаемыми экспериментальными и задаваемыми графиками, таблицами или приближенными аналитическими выражениями являются:

-вольтамперная характеристика (ВАХ) РНЭ – u (i)

-вебер-амперная характеристика ИНЭ – Y (i) – магнитная характеристика нелинейных индуктивных элементов

-кулон-вольтная характеристика ЕНЭ – q (u) электрическая характеристика емкостных нелинейных элементов.

Причиной нелинейности характеристик элементов является нелинейность параметров этих элементов – R, L, C.

Параметры этих нелинейных элементов (НЭ) – сопротивление, индуктивность, емкость – зависят от величин и направлений тока и напряжения этих элементов. Причиной этого является зависимость:

- удельной проводимости g (удельного сопротивления r) от режима цепи

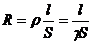
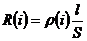или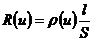

- магнитной проницаемости среды m, в которой замыкаются силовые линии магнитного поля от тока, возбудившего это поле (от напряженности поля)

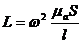
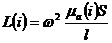
- диэлектрической проницаемости вещества, заполняющего пространство между обкладками конденсатора, от напряжения между обкладками (от напряжения электрического поля)

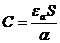
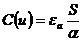
Для оценки характера изменения НЭ вводят понятие статического и дифференциального сопротивлений.

Статическое сопротивление Rст характеризует поведение НРЭ при неизменном режиме. В рассматриваемой точке ВАХ численно равно тангенсу угла наклона между осью ординат (осью токов) и прямой, соединяющей начало координат и рассматриваемую точку ВАХ, умноженного на масштаб

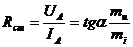
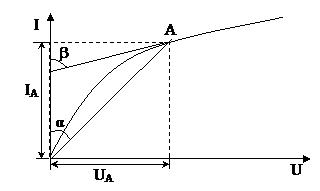
Дифференцированное сопротивление Rдиф определяет крутизну ВАХ в рассматриваемой точке и характеризует поведение НРЭ при малых отклонениях от режима в рассматриваемой точке ВАХ. Rдиф численно равно тангенсу угла наклона между осью ординат и касательной к ВАХ в рассматриваемой точке, умноженного на масштаб.

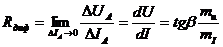
а) При последовательном соединении нескольких НРЭ Rдиф результирующей характеристики при каком-то токе равно сумме Rдиф этих НРЭ при этом же токе (т.к. производная суммы равна сумме производных)

б) Если ВАХ НРЭ имеет падающий участок, то Rдиф на этом участке отрицательно.

Примеры нелинейных элементов и их характеристик

Неуправляемые

РНЭ – лампа накаливания (1) – с ростом температуры сопротивление растет, характеристика симметричная.

- (2) тиритовые сопротивления (из керамического материала – тирита) – тиритовые разрушаются от высокого напряжения;

- терферисторы – для компенсации изменения сопротивления приборов от температуры;

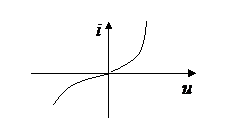
- (3) бареттер – стальная проволока в водороде (80мм рт ст) – для стабилизации тока;

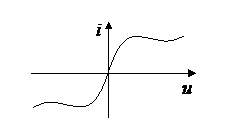
- (4) диод (несимметричная характеристика), стабилитрон

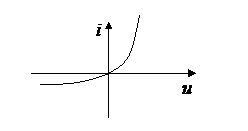
Управляемые

- транзистор – характеризуется семейством характеристик;

- ИНЭ – дроссель – катушка индуктивности с обмоткой, намотанной на замкнутый сердечник из ферромагнитного материала;

- ЕНЭ – конденсатор, между обкладками которого сегнетодиэлектрик (впервые эти свойства обнаружены у сегнетовой соли).

Особенности анализа цепей с НЭ

1. Электрическое состояние цепей с НЭ описывается системой нелинейных алгебраических уравнений (для цепей постоянного тока) и нелинейных дифференциальных уравнений (для цепей изменяющегося тока), не имеющих общего, точно-аналитического решения.

2. К цепям с НЭ не применим принцип наложения (при наложении процессов режим в цепи изменяется, а, следовательно, меняются параметры цепи).

3. Для анализа НЦ используются частные методы решения нелинейных уравнений, которые делятся на графические и аналитические.

Графические методы основываются на графических построениях с использованием ВАХ НЭ, представленного в виде графика или таблицы, и простейших расчетах.

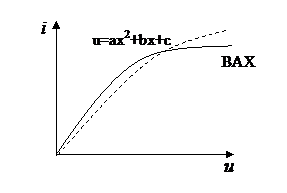
Аналитические методы основаны:

- на приближенной замене (аппроксимации) ВАХ НЭ в пределах рабочего участка аналитическим выражением с последующим аналитическим расчетом искомых величин; в частности, замена прямой линией – линеаризация;

- численные методы решения нелинейных уравнений (например, итерация);

- кусочно-линейной аппроксимации – замене ВАХ НЭ на ряд прямолинейных участков с «прикасовыванием» решений на границе участка.

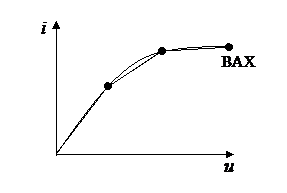
Достоинства графических методов – простота, наглядность, легкость учета особенностей ВАХ (например, гистерезисных явлений).

Недостаток – дает частное решение задачи при определенных параметрах цепи.

Достоинства аналитических методов – возможность получения решения в общем виде, что позволяет исследовать полученное решение при изменении любого из параметров цепи.

Недостаток – аналитическая аппроксимация ВАХ связана с некоторой погрешностью, что дает в результате решение с известной степенью приближения.

Описанный подход к анализу нелинейных цепей в равной степени справедлив как для цепей постоянного, так и для цепей переменного тока.