Торможение потока в прямом скачке уплотнения

Рассмотрим процесс движения ударной волны, когда скачок уплотнения уже сформировался. Допустим, это произошло, как показано на рис.9.4, в момент времени t на расстоянии от поршня х. Скорость движения поршня w, скорость распространения ударной волны u.

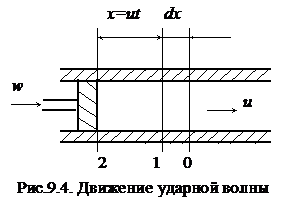
Для заторможенного потока

.

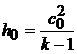Так как скорость звука в критическом сечении сопла Лаваля

,

.

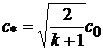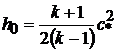Уравнение Бернулли для газового потока имеет вид

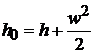или .

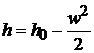При пересечении потока газа фронта ударной волны в скачке уплотнения происходят необратимые потери энергии, которая рассеивается в виде тепловой энергии. Однако при этом энтальпия газового потока остается неизменной, поэтому также не меняются и температура торможения Т₀, скорости звука в заторможенном и критическом состоянии с₀, с_* и температура газа в критическом состоянии Т_*.

Запишем уравнение Бернулли для областей до и после скачка уплотнения:

. (9.31)

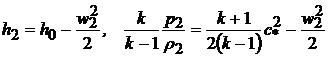. (9.32)

Отсюда

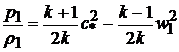, (9.33)

. (9.34)

Подставим (9.33) и (9.34) в (9.28). Получим

.

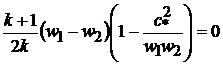Отсюда следует, что 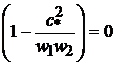или

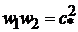. (9.35)

Это выражение, полученное Прандтлем, можно представить в безразмерном виде

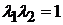. (9.36)

Отсюда видно, что при сверхзвуковой скорости до скачка (l₁ > 1) поток после скачка уплотнения становится дозвуковым (l₂ < 1).

Можно показать, что изменение полного давления в потоке газа, учитывающее волновое сопротивление, определяется выражением

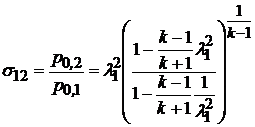. (9.37)

Сужающиеся сопла

Для реализации течения в соплах необходим некоторый перепад давления, т. е. выполнение условия 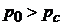. В зависимости от относительной величины перепада, т.е. от отношения 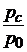на выходе из сопла скорость газа может быть меньше или больше скорости звука. Для получения сверхзвукового потока необходимо, чтобы выполнялось условие

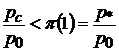. (10.1)

Для воздуха 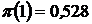, для перегретого пара 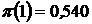. При меньшем перепаде давления, т.е. при 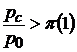возможен только дозвуковой поток. Для таких режимов применяются сужающиеся сопла, у которых площадь сечения 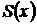уменьшается по длине сопла, т.е. .

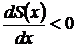В дальнейшем будем рассматривать только прямые задачи, в которых необходимо рассчитать течение газа в сопле или выбрать его характерные размеры для обеспечения требуемого расхода газа, считая общий вид контура сопла заданным.

При отсутствии потерь на трение скорость газа на выходе из сужающегося сопла однозначно определяется параметрами торможения газа перед соплом р₀, Т₀ и давлением газа за соплом р_с. Поэтому расчет сводится к определению площади выходного сечения сопла S_с для обеспечения требуемого расхода газа G_с.

Из уравнения неразрывности, которое справедливо для любого сечения сопла,

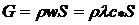(10.2)

следует, что площадь сечения сопла S равна

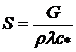. (10.3)

Давление торможения потока р₀ и давление за соплом р_с связаны с приведенной скоростью потока на выходе из сопла соотношением

,

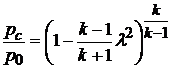откуда

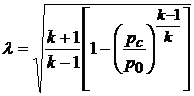. (10.4)

Для изоэнтропного адиабатического течения плотность газа за соплом будет равна

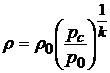. (10.5)

Скорость звука в критическом сечении-

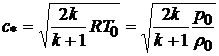. (10.6)

Расчет сопла производится в следующей последовательности. Сначала находится отношение 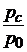, затем проверяется условие (10.1). Если давление за соплом ниже критического, то принимается 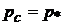. Далее по (10.4) находится приведенная скорость газа на выходе из сопла l_с, по (10.5) рассчитывается плотность газа на выходе из сопла, по (10.6) находится критическая скорость газа и по (10.3) вычисляется площадь выходного сечения сопла.

Газодинамические функции позволяют упростить расчет сопел. Сначала вычисляется значение газодинамической функции давления

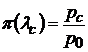(10.7)

и проверяется выполнение условия

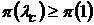. (10.8)

Если это условие не выполняется, то принимается

.

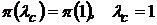Далее по таблицам газодинамических функций по величине 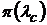находится значение приведенной скорости l_с и значение функци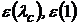й и 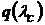. Затем по (10.6) рассчитывается скорость звука в критическом сечении с_*. Так как площадь критического сечения сопла равна

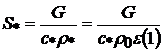, (10.9)

при этом

,

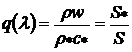то площадь выходного сечения сопла находится по формуле

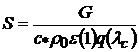. (10.10)

При снижении давления за соплом р_с и сохранении давления р₀ приведенное давление 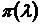снижается, скорость на выходе из сопла l_с увеличивается и возрастает расход газа G. Эта тенденция продолжается до тех пор, пока скорость газа на выходе из сопла не достигнет скорости звука. После этого на выходе из сопла устанавливается давление р_*, соответствующее критическому режиму, и дальнейшее снижение давления за соплом перестает оказывать влияние на режим истечения из сопла. Происходит так называемое запирание сопла.

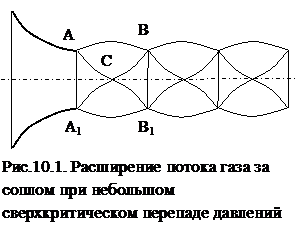При сверхкритических перепадах давлений дальнейшее расширение потока происходит в струе за соплом. Наблюдается следующая картина, показанная на рис.10.1.

Кромка выходного сечения является источником возмущения для звукового потока. За выходным сечением струи струя с давлением р_* встречает давление среды р_а, которое меньше критического. По контуру АА₁ давление меняется от р_* до р_а. Волны разрежения проходят по линиям АВ и АВ₁, А₁В₁ и А₁В. Так как эти волны пересекаются, то линии разрежения искривляются.

В конусе АСА₁ поток настолько интенсивно расширяется, что давление в точке С становится меньше давления среды р_а. Линии АВ и А₁В₁, разделяющие поверхности газовой струи и неподвижной среды, сначала расширяются, а затем начинают сужаться. В конусе ВСВ₁ происходит сжатие газового потока до давления р_*. Затем процесс повторяется, давление в струе меняется по некоторому периодическому закону, близкому к синусоидальному.

Вследствие вязкости газа, которая не учитывается в модели идеальной жидкости, к струе подсасывается газ из окружающей среды, струя расширяется, конусы разрежения и сжатия становятся менее интенсивными, колебательный процесс затухает и на некотором расстоянии от сопла в струе газа устанавливается давление р_а. За счет потерь на трение полное давление газового потока снижается.

При увеличении давления перед соплом или снижении давления за соплом структура потока перестраивается. Углы волн АВ₁ и А₁В уменьшаются, клинья АСА₁ и ВСВ₁ растягиваются, расстояние между сечениями АА₁ и ВВ₁ увеличивается. Такая перестройка продолжается до определенного предела. Начиная с некоторого предельного отношения давлений газа до и после сопла, структура потока существенно меняется, как показано на рис.10.2.

Из-за интенсивного уменьшения давления газа в пределах конуса разрежения в ядре поток разгоняется до сверхзвуковой скорости, который тормозится в прямом скачке уплотнения СС₁ и криволинейных скачках СВ и С₁В₁.

При пересечении прямого скачка СС₁ поток становится дозвуковым, а давление возрастает до 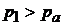. При переходе через скачки СВ и С₁В₁ скорости остаются сверхзвуковыми. В результате взаимодействия с внешним сверхзвуковым потоком дозвуковое ядро ускоряется, его сечение уменьшается до минимального значения DD₁, в котором достигается скорость звука.

Сопло Лаваля

При сверхкритических перепадах, когда 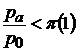, возможно получение сверхзвукового потока. Для этой цели используются сопла Лаваля, состоящие из сужающейся части, где газовый поток ускоряется до скорости звука, и расширяющейся части, где происходит дальнейшее ускорение уже сверхзвукового потока. Определяющим параметром сопла Лаваля является площадь критического сечения, в котором достигается скорость звука. Эта площадь находится по формуле (10.9)

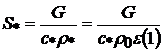
Для критического сечения скорость газа равна скорости звука в этом сечении, рассчитываемой по формуле

.

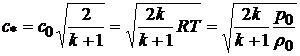Для цилиндрического сопла диаметр критического сечения

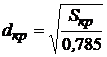. (10.11)

Вторым характерным размером сопла Лаваля является площадь его выходного сечения S_к. При расчетном режиме работы в этом сечении давление статическое давление в газовом потоке становится равным конечному давлению р_а. Скорость газа в этом сечении можно найти из уравнения

,

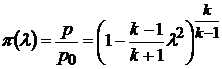откуда

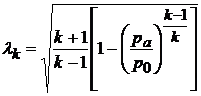. (10.12)

Для сокращения вычислений величину l_к можно найти по таблице газодинамических функций из условия

.

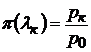Скорость газа в выходном сечении сопла

.

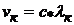Температура газа и его плотность находятся по формулам

,

,

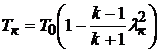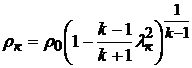или находятся с помощью таблиц газодинамических функций по формулам

,

.

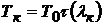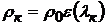Площадь выходного сечения сопла и диаметр находятся по уравнениям

, .

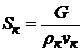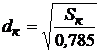Для заданной конфигурации сопла параметры потока в различных сечениях можно найти с помощью газодинамических функций. Для контрольного сечения площадью S_x определяется величина

,

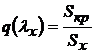а затем по ней находятся величины 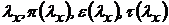и параметры потока

,

,

,

.

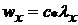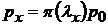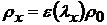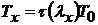Для расчетного режима можно подобрать размеры сопла Лаваля таким образом, чтобы при заданном расходе газа G давление газа на выходе из сопла р_к точно соответствовало бы давлению среды р_а. Однако оборудование часто работает в режимах, отличающихся от расчетных. В этом случае могут меняться как параметры газа перед соплом, так и параметры среды в выходном сечении сопла. Такие режимы называются нерасчетными.

Для сопла Лаваля существуют два нерасчетных режима, при которых давление газа в выходном сечении сопла больше давления среды 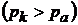или меньше давления среды 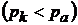. Первый режим называется режимом с недорасширением. В этом случае процесс дальнейшего выравнивания давлений происходит на некотором удалении от сопла по схеме, показанной на рис.10.2. В результате нескольких прямых и косых скачков уплотнения, в которых происходит рассеяние энергии с потерей полного давления, поток выравнивается, а его скорость становится близкой к скорости на срезе сопла.

В том случае, если площадь выходного сечения сопла для данного режима оказывается слишком большой, то на выходе из сопла давление газового потока оказывается меньше давления окружающей среды. Такой режим называется режимом с перерасширением. Схема движения газа за соплом показана на рис.10.3.

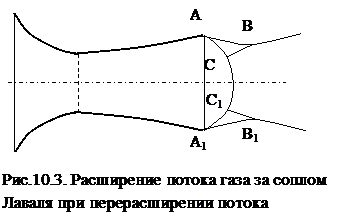Сверхзвуковой поток, встречаясь с неподвижной средой, скачком тормозится. Скачки начинаются с кромок сопла по контуру АА₁. Так как внутри потока за соплом волны сжатия пересекаются, то поверхность внутреннего скачка является криволинейной. На выходе из сопла в объеме, ограниченном контуром АСС₁А₁А поток сверхзвуковой. В объемах АСВ и А₁С₁В₁ скорость газа меньше скорости звука. Ударная волна образуется только на поверхности СС₁. За счет того, что при прохождении фронта волны поток сжимается, и его давление становится выше давления среды, по контуру ВСС₁В₁ он снова начинает разгоняться до сверхзвуковой скорости. Структура потока повторяется в следующей группе скачков.

При снижении давления среды скачки давления перемещаются вглубь сопла, и из сопла выходит дозвуковой поток. В этом случае выходная часть сопла за фронтом ударной волны работает как простой дозвуковой диффузор. При еще большем противодавлении скачок перемещается к критическому сечению сопла, скачки исчезают, и сопло Лаваля начинает работать в дозвуковом режиме как труба Вентури.