Понятие интегралов на поверхности

ПОНЯТИЕ ИНТЕГРАЛОВ НА ПОВЕРХНОСТИ

Поверхностный интеграл первого рода

Пусть непрерывная функция задана на гладкой поверхности σ. (Гладкой называется поверхность, имеющая в каждой своей точке касательную плоскость, положение которой меняется непрерывно при переходе от точки к точке.) Для вычисления поверхностного интеграла первого рода по поверхности σ, заданной уравнением где – дифференцируемая функция, предположим, что поверхность σ однозначно проектируется на плоскость 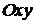в область D. Поскольку , то получим:

.

Итак, вычисление поверхностного интеграла первого рода свелось к вычислению соответствующего двойного интеграла по области D – проекции поверхности σ на плоскость .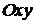

Понятие о двусторонней поверхности

Пусть σ – некоторая гладкая поверхность. Зафиксируем на ней точку и одно из двух направлений нормали к ней в этой точке, указав единичный вектор n, отложенный из . Проведем через точку замкнутую линию Г, целиком лежащую на поверхности σ и не имеющую общих точек с границей σ. Будем совершать обход линии Г так, чтобы нормаль изменялась непрерывно, при этом вектор n в каждой точке М будет иметь вполне определенное направление (вообще говоря, отличное от направления в точке ). По возвращении в точку после совершения обхода может оказаться: 1) вектор n принял первоначальное направление; 2) вектор n изменил направление на противоположное.

Поверхность σ называется двусторонней, если обход по любой замкнутой линии, лежащей на этой поверхности и не имеющей общих точек с ее границей, не меняет направления нормали к поверхности.

Двусторонней поверхностью является всякая гладкая поверхность, определяемая уравнением . Действительно, выбрав направление нормального вектора n₁ к ней так, чтобы он составил с осью острый угол, получим одну сторону поверхности (верхнюю). Выбрав это направление так, чтобы нормальный вектор n₂ составил с осью тупой угол, получим

другую сторону поверхности (нижнюю). В частности, плоскость и всякая ее часть (круг и т. п.) – двусторонняя поверхность. Любая замкнутая поверхность, не имеющая точек самопересечения (сфера, эллипсоид и др.), также является двусторонней. В самом деле, направив нормальный вектор внутрь объема, ограниченного этой поверхностью, получим одну сторону поверхности (внутреннюю), направив нормаль вне указанного объема, – другую сторону поверхности (внешнюю).

Двустороннюю поверхность называют также ориентируемой, а выбор ее определенной стороны – ориентацией поверхности.

Если на поверхности существует замкнутая линия, обход по которой меняет направление нормали, то поверхность называется односторонней. Простейшим примером односторонней поверхности является лист Мёбиуса.

ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

Скалярное поле

Векторное поле

● Векторным полем называется часть пространства, в каждой точке которого задана векторная величина (силовое поле, поле скоростей текущей жидкости и др.).

Пусть векторное поле образовано вектором

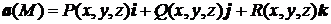
● Потоком вектора ачерез поверхность σ называется поверхно-стный интеграл вида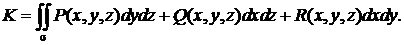
В случае, когда векторное поле 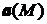представляет поле скоростей текущей жидкости, то величина потока K определяет количество жидкости, протекающее через поверхность σ.

● Дивергенция или расходимость векторного поля а в любой его точке М выражается формулой:

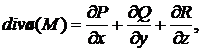
где значения частных производных берутся в точке М.

● Теорема Остроградского–Гаусса

Поток вектора а изнутри замкнутой поверхности σ равен тройному интегралу по объему V, ограниченному этой поверхностью, от дивергенции векторного поля: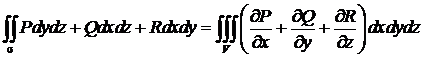

● Работа в силовом поле 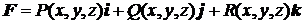вдоль кривой 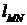находится с помощью криволинейного интеграла по формуле

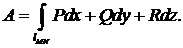
Если l замкнутый контур, то криволинейный интеграл 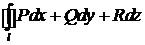называется циркуляцией.

● Ротором (вихревым вектором) векторного поля 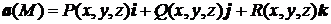называется вектор

.

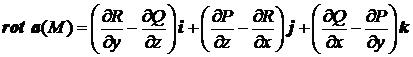Замечание. Удобно координаты вектора 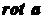находить с помощью специального определителя: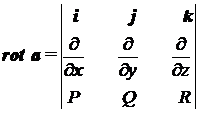

● Теорема Стокса

Поток ротора поля через поверхность σ равен циркуляции вектора по границе l этой поверхности.

.

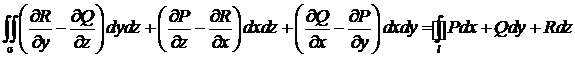Замечание. Направление интегрирования по контуру l и направление нормали n к поверхности σ согласованы так, что с конца нормали n обход вдоль контура l виден против хода часовой стрелки.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Основные понятия

● Уравнение, связывающее независимую переменную х, искомую функцию и ее производные, называется дифференциальным. Порядком дифференциального уравнения называется наивысший из порядков входящих в это уравнение производных искомой функции. Например, уравнения и – первого порядка; уравнения и – второго порядка; уравнение – четвертого порядка. Общий вид уравнения n-го порядка

(1)

В частности, это уравнение, разрешенное относительно старшей производной, примет вид

(2)

● Решением дифференциального уравнения называется функция , которая после подстановки ее и ее производных превращает уравнение в тождество. График решения дифференциального уравнения называется интегральной кривой.

● Задача Коши: найти решение уравнения (2), удовлетворяющее условиям …, (начальные условия).

Можно показать, что при определенных требованиях к правой части уравнения (2) данная задача (задача Коши) имеет единственное решение. Рассмотрим эти требования, например, для дифференциального уравнения первого порядка (3)

Теорема Коши (существования и единственности решения). Если правая часть уравнения (3) и ее частная производная определены и непрерывны в некоторой области D изменения переменных х и у, то, какова бы ни была внутренняя точка этой области, данное уравнение имеет единственное решение , которое при принимает заданное значение .

Геометрический смысл теоремы Коши следующий: через каждую внутреннюю точку области D проходит единственная интегральная кривая.

Дадим теперь определение общего и частного решений дифференциального уравнения (3), правая часть которого удовлетворяет в некоторой области D условиям теоремы Коши.

● Функция , зависящая от аргумента х и произвольной постоянной С, называется общим решением уравнения (3) в области D, если она удовлетворяет двум условиям:

1) при любых значениях произвольной постоянной С, принадлежащих некоторому множеству, функция является решением уравнения (3);

2) какова бы ни была точка , лежащая внутри области D, существует единственное значение постоянной такое, что решение удовлетворяет начальному условию: .

Всякое решение уравнения (3), получающееся из общего решения при конкретном значении , называется частным решением.

Если общее решение дифференциального уравнения найдено в виде, не разрешенном относительно у, т. е. в виде , то оно называется общим интегралом уравнения.

Виды рядов

1) Если где то

–

называется числовым рядом.

2) Если где то – функциональный ряд.

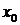3) Если где – фиксированная точка;

– числа, то – степенной ряд.

4) В случае, когда 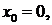степенной ряд принимает вид

12.2. Числовые ряды.
Признаки сходимости числовых рядов

Ряды Тейлора

12.5.1. НЕОБХОДИМОЕ УСЛОВИЕ РАЗЛОЖЕНИЯ ФУНКЦИИ
В РЯД ТЕЙЛОРА

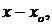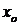(по степеням где – фиксированная точка). Если непрерывная функция 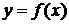бесконечное число раз дифференцируема в окрестности точки 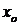, то она может быть представлена в виде ряда Тейлора:

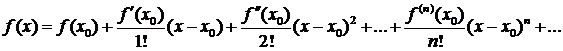
12.5.2. ДОСТАТОЧНОЕ УСЛОВИЕ РАЗЛОЖЕНИЯ ФУНКЦИИ
В РЯД ТЕЙЛОРА

называется достаточным условием сходимости ряда Тейлора к порождающей его функции и заключается в следующем. Чтобы ряд Тейлора сходился к порождающей его функции 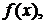т. е. сумма ряда Тейлора совпадала с данной функцией: 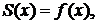достаточно, чтобы 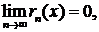где остаточный член 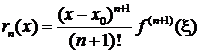и 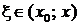(форма Лагранжа).

Пример. Разложить в ряд Тейлора функцию 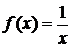по степеням .

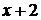Решение. Запишем ряд Тейлора для данной функции при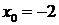

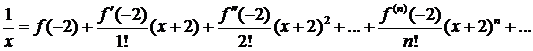
и вычислим значения данной функции и ее производных в точке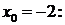

……………….. ……………….

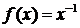
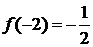
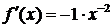
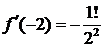
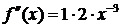
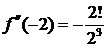
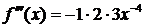
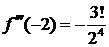
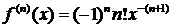
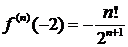
Найденные значения подставим в ряд Тейлора и получим разложение данной функции по степеням :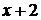

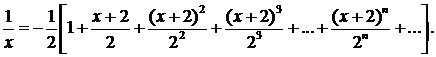
Исследуем сходимость этого ряда по признаку Даламбера:

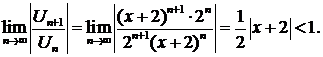
Решая последнее неравенство, находим интервал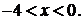

Границы этого интервала исследуем особо.

Подставляя в ряд 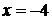, затем 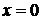, получим числовые ряды 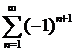и 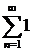, которые расходятся, так как для каждого из этих рядов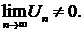

Следовательно, интервал сходимости полученного ряда Тейлора для функции 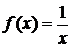есть промежуток .

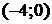Замечание. Исследуя остаточный член 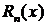формулы Тейлора, можно убедиться, что полученный ряд сходится к данной функции именно на указанном интервале.

РЯД МАКЛОРЕНА

Если 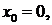то ряд Тейлора называется рядом Маклорена и разложение функции 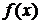в ряд Маклорена называется разложением функции по степеням х и имеет следующий вид:

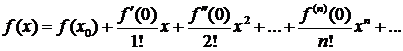
Замечание. Значение функции 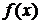и суммы ряда совпадают лишь в точках области сходимости.

РЯДЫ ФУРЬЕ

Тригонометрический ряд (1),

коэффициенты которого определяются формулами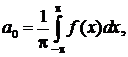

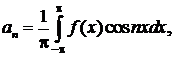
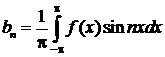
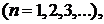(2)

называется рядом Фурье, а числа 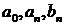– коэффициентами Фурье функции 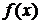. Ряд Фурье, построенный для функции 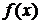, обозначается так:

.

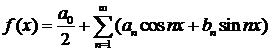● Большое практическое значение имеет следующая задача: по заданной периодической функции 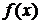с периодом 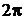найти всюду сходящийся ряд (1), имеющий сумму 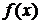. Эта задача называется разложением данной функции 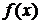в ряд Фурье.

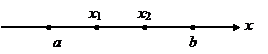● Если отрезок 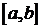можно разбить внутренними точками 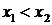так, что на каждом из полученных промежутках 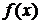и 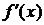будут непре-

рывны и, кроме того, существуют конечные односторонние пределы 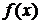и

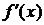в концевых точках этих промежутков, то такая функция 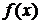называется кусочно-дифференцируемой. Кусочно-дифференцируемая на отрезке 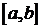функция может быть на нем непрерывной или иметь конечное число точек разрыва первого ряда.

13.1. Достаточное условие разложения
функции в ряд Фурье

Если функция 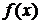кусочно-дифференцируема на отрезке 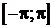, то ее ряд Фурье сходится в каждой точке 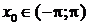, и имеет сумму

.

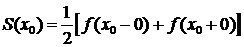На концах отрезка сумма ряда Фурье определяется формулой:

.

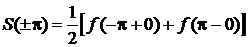Кроме того, если 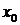– точка непрерывности 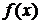, то

.

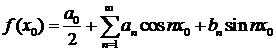Пример 18. Разложить в ряд Фурье периодическую и заданную в интервале 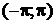функцию 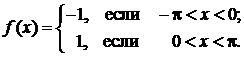Построить график функции и второй частичной суммы 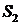ее разложения в ряд Фурье.

Решение. Данная функция имеет одну точку разрыва первого рода при 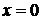, а точки экстремума отсутствуют. Следовательно, данная функция удовлетворяет условиям Дирихле и может быть представлена рядом Фурье.

Интервал 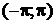симметричен относительно начала координат и на этом интервале 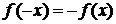, следовательно, данная функция нечетная и ее ряд Фурье не содержит косинусов, так как коэффициенты Фурье .

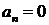Найдем коэффициенты :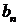

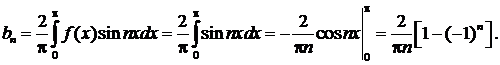
Разложение данной функции в ряд Фурье запишется следующим образом:

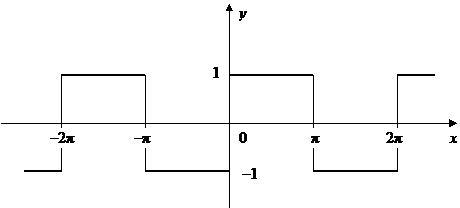Далее построим график данной функции (рис. 46, а).

Рис. 46, а

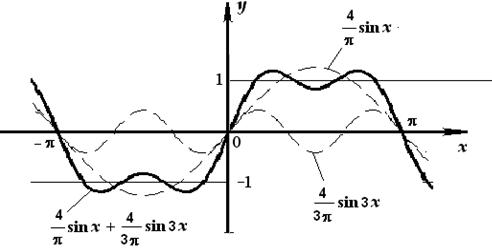
Для того чтобы выяснить, каким образом график функции приближается графиками последовательных частичных сумм полученного ряда, изобразим на рисунке графика самой функции последовательные гармоники ряда (пунктиром) и график 1-й и 2-й частичных сумм (рис. 46, б). Как видно из этого рисунка, чем больше последовательных гармоник ряда включает в себя частичная сумма, тем ближе график частичной суммы подходит к графику данной функции.

13.2. Ряд Фурье для функции, заданной на отрезке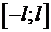

,

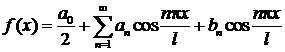где ,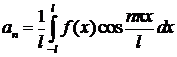

.

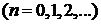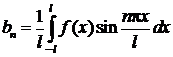
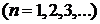Замечание. Условия сходимости ряда Фурье для функции 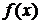, заданной на отрезке 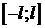аналогичны условиям разложения функции в ряд Фурье на отрезке .

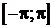Пример 19. Разложить в ряд Фурье в указанном интервале функцию:

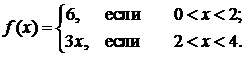
Решение. Вопрос о четности или нечетности данной функции не рассматриваем, так как она задана на интервале, не симметричном относительно начала координат. Длина указанного интервала (0,4) равна 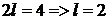. Определим коэффициенты Фурье для этой функции:

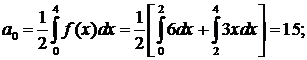
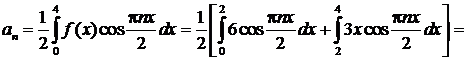
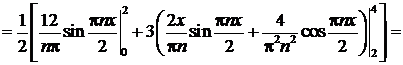
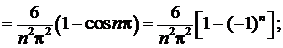
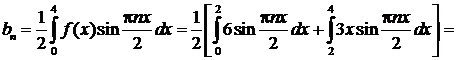
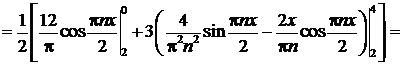
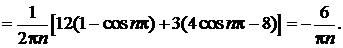
Ряд Фурье данной функции имеет вид:

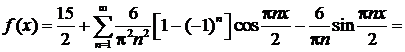
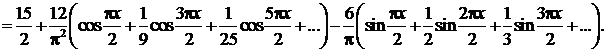
Полученное разложение справедливо во всей области определения заданной функции, причем в интервале (0,2) сумма ряда 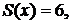а в интервале (2,4) сумма ряда 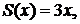так как во всех точках непрерывности сумма ряда равна исходной функции. В точке разрыва 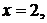где функция не определена, сумма ряда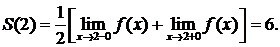

ПОНЯТИЕ ИНТЕГРАЛОВ НА ПОВЕРХНОСТИ