Обобщенный метод наименьших квадратов.
Введение в эконометрику.
Эконометрика – это математическая наука, изучающая экономическую жизнь с помощью математических методов и, преимущественно, методов математической статистики.
Цели эконометрики: эконометрический анализ данных наблюдений и вывод обоснованных практических решений.
Основным объектом изучения эконометрики является эконометрическая модель.
Основные этапы эконометрического анализа:
1. Постановочный этап – этот этап включает в себя определение конечных целей анализа, набора факторов и переменных, описание взаимосвязей между ними, а также роли этих факторов и переменных.
На этом этапе первым делом следует выяснить, какие факторы являются входными, т.е. такими, которые полностью или частично регулируемы, легко поддаются прогнозу и регистрации. Входные факторы в эконометрике называются объясняющими.
Затем определяются выходные факторы, которые трудно поддаются прогнозу, и значения которых формируются в процессе функционирования рассматриваемой системы. Выходные факторы также называются объясняемыми.
2. Априорный (предмодельный) этап– этот этап состоит в предварительном анализе содержательной сущности моделируемых явлений, в формировании и математической формализации имеющейся априорной (предварительной) информации о данном явлении в виде ряда гипотез и математических соотношений.
3. Информационно-статистический(практический) этап – на этом этапе происходит сбор необходимой статистической информации: регистрация конкретных значений определенных ранее переменных и факторов.
4. Спецификация модели– на данном этапе определяется структура модели, т.е. её символическая математическая запись, в которой, наряду с переменными и факторами, значения которых известны, обычно присутствуют величины, содержательный смысл которых определен, а числовые значения – нет.
Такие величины называются параметрами модели и их значения нужно найти.
5. Идентификация модели (id) – этот этап предназначен для проведения статистического анализа модели.
При выполнении данного этапа вначале нужно ответить на вопрос: возможно ли, в принципе, однозначно восстановить значение неизвестных параметров модели по имеющимся статистическим данным?
Если ответ положителен, то необходимо решить проблему идентификации модели, т.е. нужно предложить и реализовать математически корректную процедуру оценивания неизвестных параметров модели.
Если ответ отрицателен, то необходимо вернуться к этапу №4 и внести изменения в структуру. Но, возможно, придется вообще вернуться к этапу №2 и выбрать другую модель.
6. Верификация модели (статистический анализ точности и адекватности модели) – на данном этапе используются различные процедуры сопоставления модельных выводов (выводов по модели), оценок и следствий с реально наблюдаемой действительностью.
Если результат сопоставления неудовлетворительный, то следует вернуться на этапы №4 и №5.
Эконометрическая система «Черный ящик».
Входные факторы Выходные факторы
| «Черный ящик», в котором происходит весь эконометрический анализ. |
x2 y2
x3 y3
xn ym
Типы эконометрических моделей:
1. Модель с одним уравнением – эта модель получается при m=1, т.е. при одном зависимом факторе, следовательно,
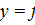 (
( 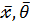 ), где
), где 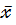 = (
= ( 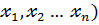 ,
,
а 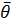 - параметры модели,
- параметры модели, 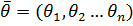
В этой модели в зависимости от функции f, различают также линейные и нелинейные модели.
Например: 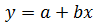 – линейная модель
– линейная модель
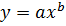 – нелинейная модель
– нелинейная модель
2. Модель с несколькими одновременными уравнениями - эта модель получается при m 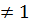 , т.е. с множеством зависимых факторов, следовательно,
, т.е. с множеством зависимых факторов, следовательно,
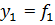 (
( 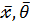 ), где
), где 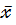 = (
= ( 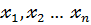 )?
)?
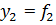 (
( 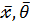 ), а
), а 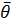 - параметры модели,
- параметры модели,
. . . при 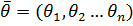
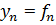 (
( 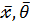 ).
).
Важной отличительной особенностью этой системы уравнений является возможность включения объясняемых переменных в число объясняющих, т.е.
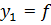 (
( 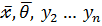 ), где ), где
), где ), где 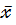 = (
= ( 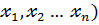 ,
,
а 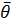 - параметры модели,
- параметры модели, 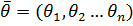
3. Временные ряды - это схема «черный ящик» с n=1, т.е. входной фактор всего один и это – время, следовательно,
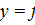 (
( 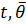 ), где t - время,
), где t - время,
а 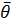 - параметры модели,
- параметры модели, 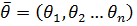
Постановки задач в эконометрике.
Предположим, что у нас есть A I – объекты исследования, при i = 1 ,2…N
X1, X2 …XN – переменные, которые описывают эти объекты. Эти переменные делятся на два типа: независимые (объясняющие, входные) и зависимые (объясняемые, выходные). Также они бывают количественными и качественными (дискретными).
Изначально, для постановки задачи, среди всех факторов и переменных следует выделить Y – зависимую переменную.
Цель эконометрического анализа – прогнозирование значения Y. Эта задача решается по-разному, в зависимости от типа переменных:
Iй вариант: все переменные X ( 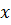 1,
1,  2…
2…  n) и Y (
n) и Y ( 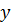 1,
1, 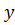 2…
2… 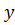 n) количественные => для решения применяются методы регрессионного анализа.
n) количественные => для решения применяются методы регрессионного анализа.
IIй вариант: все переменные X ( 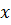 1,
1,  2…
2…  n)– количественные, а все Y(
n)– количественные, а все Y( 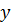 1,
1, 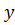 2…
2… 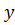 n) – качественные (дискретные) => для решения применяются методы классификации, распознавания образов и дискриминантный анализ.
n) – качественные (дискретные) => для решения применяются методы классификации, распознавания образов и дискриминантный анализ.
IIIй вариант: все переменные X ( 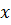 1,
1,  2…
2…  n)– качественные (дискретные), а все Y(
n)– качественные (дискретные), а все Y( 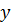 1,
1, 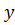 2…
2… 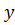 n) – количественные => для решения применяются методы дисперсионного анализа.
n) – количественные => для решения применяются методы дисперсионного анализа.
IVй вариант: одна часть переменных X ( 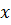 1,
1,  2…
2…  L) – количественные, а другая часть (
L) – количественные, а другая часть ( 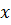 L,
L,  2…
2…  n) – качественные (дискретные), все переменные Y(
n) – качественные (дискретные), все переменные Y( 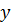 1,
1, 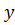 2…
2… 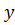 n) – количественные => для решения применяются ковариационный анализ или метод «деревья регрессии».
n) – количественные => для решения применяются ковариационный анализ или метод «деревья регрессии».
Регрессионный анализ.
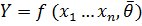 – решающая функция или функция регрессии.
– решающая функция или функция регрессии.
Замечание: 1) 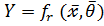 = E(Y/X), где Y и X - дискретные случайные величины.
= E(Y/X), где Y и X - дискретные случайные величины.
| Y X | b1 | b2 | …. | bn |
| a1 | P1 1 | P1 2 | …. | P1 n |
| a2 | P2 1 | P2 2 | …. | P2 n |
| …. | …. | …. | …. | …. |
| an | Pn 1 | Pn 2 | …. | Pn n |
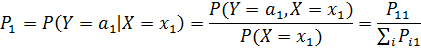
Если Y и X дискретные случайные величины, то
функция регрессии – это условное мат.ожидание.
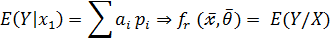
2)Если Y и X - непрерывные случайные величины
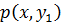 - плотность совместного распределения X и Y.
- плотность совместного распределения X и Y.
Условное распределение, следовательно и условная плотность.
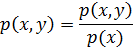
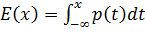 ,
, 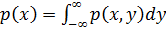
- частное распределение
Мат. ожидание: 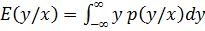
( 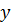 i,
i,  i)...-значения наблюдений (Y,X)
i)...-значения наблюдений (Y,X)
i=1,2,..,n
Естественно, при каждом
наблюдении возможна ошибка ( 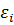 ).
).
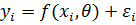
Предполагают, что 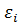 - вектор ошибок - удовлетворяет следующим условиям:
- вектор ошибок - удовлетворяет следующим условиям:
1. 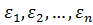 - независимые случайные величины
- независимые случайные величины
2. Е 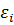 =0, D
=0, D 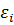 =
= 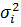 - постоянные
- постоянные
3. 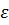 и
и 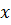 тоже независимые, т.е. ошибка от Х не зависит
тоже независимые, т.е. ошибка от Х не зависит
Этапы (шаги) регрессионного анализа:
1. выбор вида модели
2. оценка параметров выбранной модели. Оценка функций регрессии ( 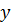 *).
*).
3.проверка статистических гипотез по регрессионной модели.
4. проверка модели на адекватность и точность.
5.эксперементальная проверка модели и прогнозирование на основе этой модели.
Виды регрессионных моделей:
1. простейшая линейная модель
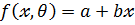 ,
, 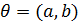 – параметры модели
– параметры модели
2. множественная линейная модель
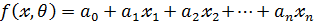
3. полиномиальная модель
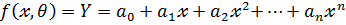
4.гипперболическая модель
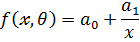
5. показательная модель
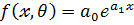
6. логистическая модель (S-образная кривая)
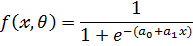
7. стапенная модель
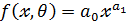
8. логарифмическая модель
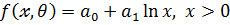
Замечание: Метод аналитической группировки.
1. Способ выбора вида модели. Графический.
| X |  | 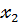 | 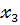 | … | 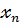 |
| Y | 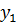 | 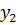 | 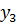 | … | 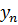 |
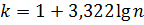 ,
, 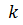 - количество интервалов
- количество интервалов
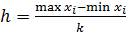 ,
, 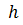 - длина интервала
- длина интервала
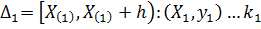
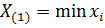
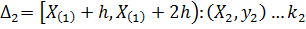
И т.д.
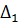 :
: 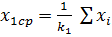
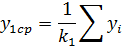
Т.е. 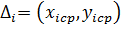 - одна средняя точка
- одна средняя точка
Далее, определив еще несколько средних точек, строим по ним график функции и по нему определяем вид модели.
2. Оценивание параметров выбранной модели (на примере линейной модели, т.к. остальные виды моделей с помощью небольших преобразований сводятся к линейной).
Примеры моделей, которые сводятся к линейным:
1. 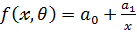 - гиперболическая модель
- гиперболическая модель
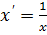 =>
=>
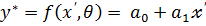
2. 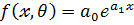 - показательная модель
- показательная модель
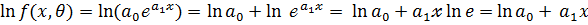
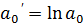 ,
, 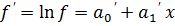 ,
, 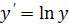
 |  | 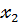 | 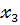 | … | 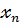 |
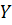 | 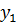 | 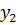 | 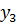 | … | 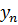 |
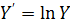 | 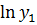 | … | … | … | 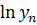 |
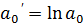 =>
=> 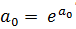 =>
=>
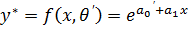
3. 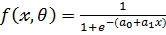 – логистическая модель
– логистическая модель
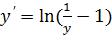 ,
, 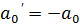 ,
, 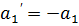 =>
=> 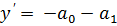 =>
=>
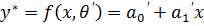
4. 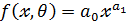 – степенная модель
– степенная модель
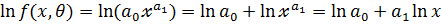 ,
, 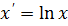 ,
, 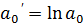 =>
=> 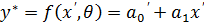
5. 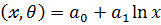 – логарифмическая модель
– логарифмическая модель
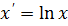 =>
=>
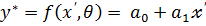
Наша регрессионная модель имеет классическую форму, т.е. удовлетворяет следующим двум условиям:
1. Переменная 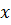 – не случайная величина, т.е. она задается (управляема),
– не случайная величина, т.е. она задается (управляема),
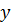 - случайная величина.
- случайная величина.
2. Случайные ошибки  независимые, одинаково распределенные случайные, имеющие нормальное распределение с нулевым математическим ожиданием (
независимые, одинаково распределенные случайные, имеющие нормальное распределение с нулевым математическим ожиданием ( 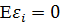 ) и
) и 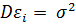
Теорема Гауса-Маркова.
(без доказательства)
Пусть выполняются условия №№ 1 и2, тогда оценки, полученные методом наименьших квадратов 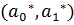 обладают следующими свойствами:
обладают следующими свойствами:
1. Они не смещенные, т.е.
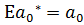 и
и 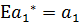
2. Дисперсия этих оценок минимальна среди всех линейных моделей, эти оценки называются эффективными.
Введение в эконометрику.
Эконометрика – это математическая наука, изучающая экономическую жизнь с помощью математических методов и, преимущественно, методов математической статистики.
Цели эконометрики: эконометрический анализ данных наблюдений и вывод обоснованных практических решений.
Основным объектом изучения эконометрики является эконометрическая модель.
Основные этапы эконометрического анализа:
1. Постановочный этап – этот этап включает в себя определение конечных целей анализа, набора факторов и переменных, описание взаимосвязей между ними, а также роли этих факторов и переменных.
На этом этапе первым делом следует выяснить, какие факторы являются входными, т.е. такими, которые полностью или частично регулируемы, легко поддаются прогнозу и регистрации. Входные факторы в эконометрике называются объясняющими.
Затем определяются выходные факторы, которые трудно поддаются прогнозу, и значения которых формируются в процессе функционирования рассматриваемой системы. Выходные факторы также называются объясняемыми.
2. Априорный (предмодельный) этап– этот этап состоит в предварительном анализе содержательной сущности моделируемых явлений, в формировании и математической формализации имеющейся априорной (предварительной) информации о данном явлении в виде ряда гипотез и математических соотношений.
3. Информационно-статистический(практический) этап – на этом этапе происходит сбор необходимой статистической информации: регистрация конкретных значений определенных ранее переменных и факторов.
4. Спецификация модели– на данном этапе определяется структура модели, т.е. её символическая математическая запись, в которой, наряду с переменными и факторами, значения которых известны, обычно присутствуют величины, содержательный смысл которых определен, а числовые значения – нет.
Такие величины называются параметрами модели и их значения нужно найти.
5. Идентификация модели (id) – этот этап предназначен для проведения статистического анализа модели.
При выполнении данного этапа вначале нужно ответить на вопрос: возможно ли, в принципе, однозначно восстановить значение неизвестных параметров модели по имеющимся статистическим данным?
Если ответ положителен, то необходимо решить проблему идентификации модели, т.е. нужно предложить и реализовать математически корректную процедуру оценивания неизвестных параметров модели.
Если ответ отрицателен, то необходимо вернуться к этапу №4 и внести изменения в структуру. Но, возможно, придется вообще вернуться к этапу №2 и выбрать другую модель.
6. Верификация модели (статистический анализ точности и адекватности модели) – на данном этапе используются различные процедуры сопоставления модельных выводов (выводов по модели), оценок и следствий с реально наблюдаемой действительностью.
Если результат сопоставления неудовлетворительный, то следует вернуться на этапы №4 и №5.
Эконометрическая система «Черный ящик».
Входные факторы Выходные факторы
| «Черный ящик», в котором происходит весь эконометрический анализ. |
x2 y2
x3 y3
xn ym
Типы эконометрических моделей:
1. Модель с одним уравнением – эта модель получается при m=1, т.е. при одном зависимом факторе, следовательно,
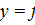 (
( 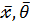 ), где
), где 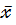 = (
= ( 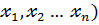 ,
,
а 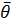 - параметры модели,
- параметры модели, 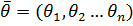
В этой модели в зависимости от функции f, различают также линейные и нелинейные модели.
Например: 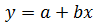 – линейная модель
– линейная модель
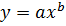 – нелинейная модель
– нелинейная модель
2. Модель с несколькими одновременными уравнениями - эта модель получается при m 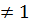 , т.е. с множеством зависимых факторов, следовательно,
, т.е. с множеством зависимых факторов, следовательно,
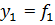 (
( 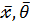 ), где
), где 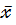 = (
= ( 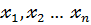 )?
)?
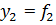 (
( 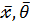 ), а
), а 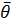 - параметры модели,
- параметры модели,
. . . при 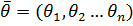
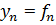 (
( 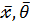 ).
).
Важной отличительной особенностью этой системы уравнений является возможность включения объясняемых переменных в число объясняющих, т.е.
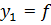 (
( 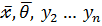 ), где ), где
), где ), где 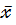 = (
= ( 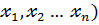 ,
,
а 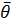 - параметры модели,
- параметры модели, 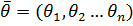
3. Временные ряды - это схема «черный ящик» с n=1, т.е. входной фактор всего один и это – время, следовательно,
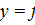 (
( 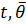 ), где t - время,
), где t - время,
а 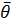 - параметры модели,
- параметры модели, 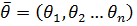
Постановки задач в эконометрике.
Предположим, что у нас есть A I – объекты исследования, при i = 1 ,2…N
X1, X2 …XN – переменные, которые описывают эти объекты. Эти переменные делятся на два типа: независимые (объясняющие, входные) и зависимые (объясняемые, выходные). Также они бывают количественными и качественными (дискретными).
Изначально, для постановки задачи, среди всех факторов и переменных следует выделить Y – зависимую переменную.
Цель эконометрического анализа – прогнозирование значения Y. Эта задача решается по-разному, в зависимости от типа переменных:
Iй вариант: все переменные X ( 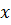 1,
1,  2…
2…  n) и Y (
n) и Y ( 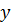 1,
1, 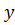 2…
2… 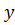 n) количественные => для решения применяются методы регрессионного анализа.
n) количественные => для решения применяются методы регрессионного анализа.
IIй вариант: все переменные X ( 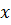 1,
1,  2…
2…  n)– количественные, а все Y(
n)– количественные, а все Y( 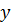 1,
1, 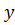 2…
2… 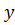 n) – качественные (дискретные) => для решения применяются методы классификации, распознавания образов и дискриминантный анализ.
n) – качественные (дискретные) => для решения применяются методы классификации, распознавания образов и дискриминантный анализ.
IIIй вариант: все переменные X ( 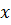 1,
1,  2…
2…  n)– качественные (дискретные), а все Y(
n)– качественные (дискретные), а все Y( 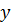 1,
1, 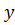 2…
2… 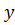 n) – количественные => для решения применяются методы дисперсионного анализа.
n) – количественные => для решения применяются методы дисперсионного анализа.
IVй вариант: одна часть переменных X ( 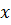 1,
1,  2…
2…  L) – количественные, а другая часть (
L) – количественные, а другая часть ( 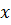 L,
L,  2…
2…  n) – качественные (дискретные), все переменные Y(
n) – качественные (дискретные), все переменные Y( 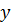 1,
1, 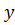 2…
2… 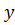 n) – количественные => для решения применяются ковариационный анализ или метод «деревья регрессии».
n) – количественные => для решения применяются ковариационный анализ или метод «деревья регрессии».
Регрессионный анализ.
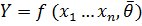 – решающая функция или функция регрессии.
– решающая функция или функция регрессии.
Замечание: 1) 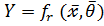 = E(Y/X), где Y и X - дискретные случайные величины.
= E(Y/X), где Y и X - дискретные случайные величины.
| Y X | b1 | b2 | …. | bn |
| a1 | P1 1 | P1 2 | …. | P1 n |
| a2 | P2 1 | P2 2 | …. | P2 n |
| …. | …. | …. | …. | …. |
| an | Pn 1 | Pn 2 | …. | Pn n |
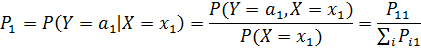
Если Y и X дискретные случайные величины, то
функция регрессии – это условное мат.ожидание.
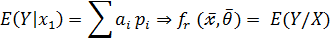
2)Если Y и X - непрерывные случайные величины
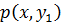 - плотность совместного распределения X и Y.
- плотность совместного распределения X и Y.
Условное распределение, следовательно и условная плотность.
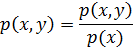
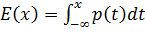 ,
, 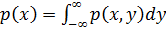
- частное распределение
Мат. ожидание: 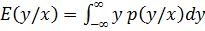
( 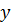 i,
i,  i)...-значения наблюдений (Y,X)
i)...-значения наблюдений (Y,X)
i=1,2,..,n
Естественно, при каждом
наблюдении возможна ошибка ( 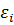 ).
).
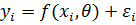
Предполагают, что 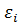 - вектор ошибок - удовлетворяет следующим условиям:
- вектор ошибок - удовлетворяет следующим условиям:
1. 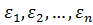 - независимые случайные величины
- независимые случайные величины
2. Е 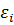 =0, D
=0, D 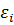 =
= 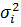 - постоянные
- постоянные
3. 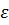 и
и 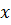 тоже независимые, т.е. ошибка от Х не зависит
тоже независимые, т.е. ошибка от Х не зависит
Этапы (шаги) регрессионного анализа:
1. выбор вида модели
2. оценка параметров выбранной модели. Оценка функций регрессии ( 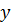 *).
*).
3.проверка статистических гипотез по регрессионной модели.
4. проверка модели на адекватность и точность.
5.эксперементальная проверка модели и прогнозирование на основе этой модели.
Виды регрессионных моделей:
1. простейшая линейная модель
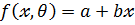 ,
, 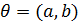 – параметры модели
– параметры модели
2. множественная линейная модель
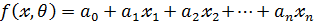
3. полиномиальная модель
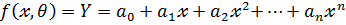
4.гипперболическая модель
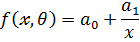
5. показательная модель
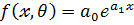
6. логистическая модель (S-образная кривая)
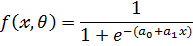
7. стапенная модель
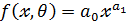
8. логарифмическая модель
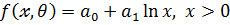
Замечание: Метод аналитической группировки.
1. Способ выбора вида модели. Графический.
| X | 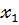 | 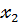 | 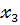 | … | 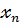 |
| Y | 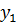 | 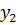 | 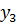 | … | 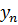 |
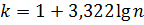 ,
, 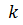 - количество интервалов
- количество интервалов
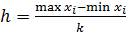 ,
, 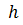 - длина интервала
- длина интервала
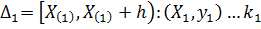
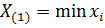
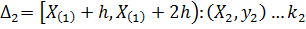
И т.д.
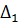 :
: 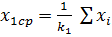
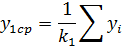
Т.е. 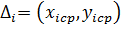 - одна средняя точка
- одна средняя точка
Далее, определив еще несколько средних точек, строим по ним график функции и по нему определяем вид модели.
2. Оценивание параметров выбранной модели (на примере линейной модели, т.к. остальные виды моделей с помощью небольших преобразований сводятся к линейной).
Примеры моделей, которые сводятся к линейным:
1. 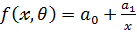 - гиперболическая модель
- гиперболическая модель
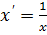 =>
=>
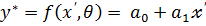
2. 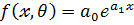 - показательная модель
- показательная модель
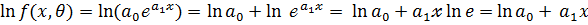
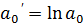 ,
, 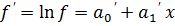 ,
, 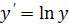
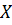 | 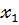 | 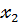 | 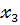 | … | 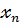 |
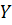 | 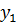 | 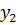 | 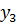 | … | 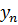 |
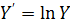 | 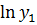 | … | … | … | 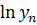 |
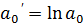 =>
=> 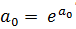 =>
=>
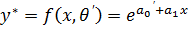
3. 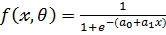 – логистическая модель
– логистическая модель
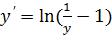 ,
, 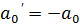 ,
, 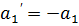 =>
=> 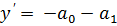 =>
=>
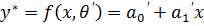
4. 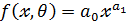 – степенная модель
– степенная модель
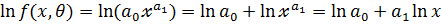 ,
, 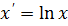 ,
, 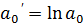 =>
=> 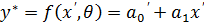
5. 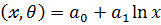 – логарифмическая модель
– логарифмическая модель
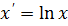 =>
=>
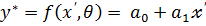
Наша регрессионная модель имеет классическую форму, т.е. удовлетворяет следующим двум условиям:
1. Переменная 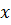 – не случайная величина, т.е. она задается (управляема),
– не случайная величина, т.е. она задается (управляема),
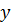 - случайная величина.
- случайная величина.
2. Случайные ошибки  независимые, одинаково распределенные случайные, имеющие нормальное распределение с нулевым математическим ожиданием (
независимые, одинаково распределенные случайные, имеющие нормальное распределение с нулевым математическим ожиданием ( 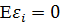 ) и
) и 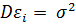
Теорема Гауса-Маркова.
(без доказательства)
Пусть выполняются условия №№ 1 и2, тогда оценки, полученные методом наименьших квадратов 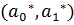 обладают следующими свойствами:
обладают следующими свойствами:
1. Они не смещенные, т.е.
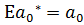 и
и 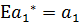
2. Дисперсия этих оценок минимальна среди всех линейных моделей, эти оценки называются эффективными.
Обобщенный метод наименьших квадратов.
Применение метода наименьших квадратов в некоторых случаях может привести к тому, что полученные оценки параметров не будут оптимальны в смысле теоремы Гауса-Маркова. Для анализа таких ситуаций обычно используют обобщенный метод наименьших квадратов для модели множественной регрессии.
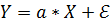 , где а - вектор параметров
, где а - вектор параметров
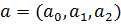
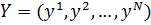
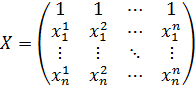 , где
, где 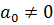
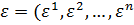 ) – ошибки наблюдений
) – ошибки наблюдений
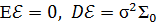 , где
, где 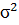 - неизвестная const,
- неизвестная const, 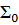 - положительно определенная матрица.
- положительно определенная матрица.
В общем виде определить трудно вид этой матрицы 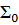 , поэтому на практике делают некоторые предположения о её структуре. Если нарушается только условие:
, поэтому на практике делают некоторые предположения о её структуре. Если нарушается только условие:
1) 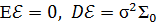 (или одно из этих равенств не выполняется), то
(или одно из этих равенств не выполняется), то
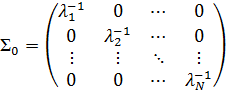 , где
, где 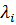 неизвестны, но могут быть оценены статистическими методами.
неизвестны, но могут быть оценены статистическими методами.
2) (условие некоррелируемости случайных ошибок), то матрица 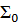 не является диагональной матрицей, т.е. вне главной диагонали есть ненулевые элементы, а на главной диагонали - только единицы.
не является диагональной матрицей, т.е. вне главной диагонали есть ненулевые элементы, а на главной диагонали - только единицы.
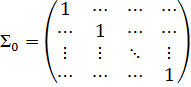
Оценивание параметров модели с помощью методов наименьших квадратов происходит следующим образом: 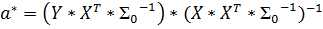 . Эти оценки являются оптимальными оценками в смысле теории Гауса-Маркова.
. Эти оценки являются оптимальными оценками в смысле теории Гауса-Маркова.
Для этой модели (множественной рег
