Формула корней квадратного уравнения.

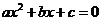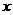О. Уравнение вида , где – переменная 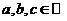, 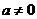называется квадратным.

О. Если 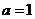, то уравнение называется приведенным квадратным уравнением.

О. Квадратное уравнение, в котором хотя бы один из коэффициентов 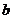или 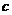равен 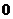, называется неполным квадратным уравнением

Выведем формулу корней квадратного уравнения в общем случае:

,

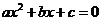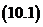
Поделим обе части уравнения на 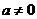. При этом корни уравнения не изменятся (почему?).

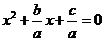
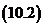
Выделим полный квадрат:

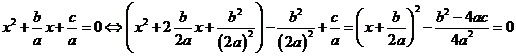
О. Выражение: 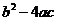называется дискриминантом квадратного уравнения, и обозначается через 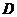, тогда уравнение можно записать так:

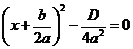
Возможны следующие 3 случая:

1.Если 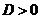, то из дискриминанта можно извлечь корень (почему?), тогда получаем решения уравнения:

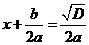или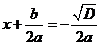

То есть

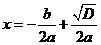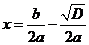
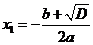или

или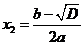

Эти две формулы можно объединить в следующую:

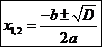- эта формула называется формулой корней квадратного уравнения

2.Если 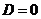, то уравнение 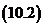примет вид:

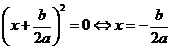
В этом случае уравнение имеет один корень.

Замечание: можно также сказать, что в этом случае квадратное уравнение имеет два совпадающих корня.

3.Если 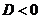, то значение дроби 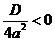, поэтому уравнение 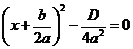, а значит и уравнение 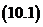не имеет корней (почему?).

Таким образом,

Если 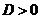, то уравнение 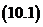имеет 2 различных корня: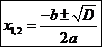

Если 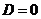, то уравнение 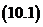имеет 2 совпадающих корня: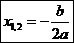

Если 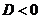, то уравнение 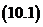корней не имеет.

Теорема Виета.

Пусть дано уравнение 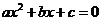, 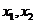– корни уравнения, тогда

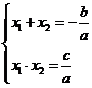
Доказательство:

Пусть уравнение 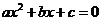имеет 2 различных корня ( ):

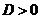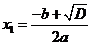
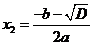
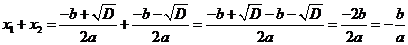
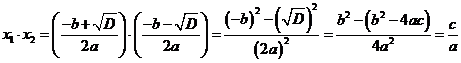
Итак, действительно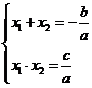

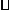
Замечание: Если рассмотреть приведенное квадратное уравнение 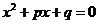, то формулы Виета будут выглядеть так: .

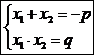В школьном курсе математики чаще всего формулы Виета применяются именно для приведенного квадратного уравнения.

Имеет место теорема, обратная теореме Виета:

Если числа 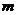и 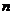таковы, что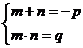

То эти числа являются корнями уравнения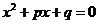

Доказательство:

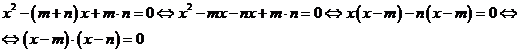
Значит, числа 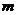и 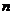действительно являются корнями уравнения .

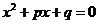Замечание: теорема, обратная теореме Виета, позволяет составлять квадратные уравнения по его корням.

Например, если 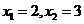, то 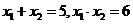, тогда эти числа являются корнями уравнения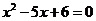

16. Разложение квадратного трехчлена на линейные множители

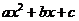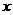О. Многочлен вида: , где – переменная 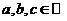, 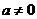называется квадратным трехчленом.

О.Корнем квадратного трехчлена называется значение переменной, при которой значение этого трехчлена равно нулю.

Теорема.

Есл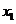и и 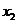– корни квадратного трёхчлена 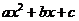, то

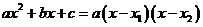
Доказательство:

Вынесем за скобки в многочлене 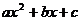множитель а.Получим: 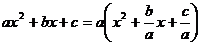. Так как корни квадратного трёхчлена 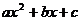являются корнями квадратного уравнения 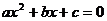, то, по теореме Виета, , .

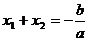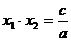Поэтому

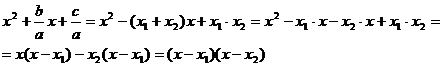
Итак,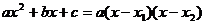

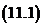
Если квадратный трёхчлен имеет один корень (два совпадающих корня), то формула 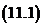примет вид 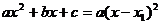, где 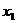- корень квадратного трёхчлена.

Заметим, что если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.

17. Формулы сокращенного умножения.

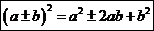
Доказательство:

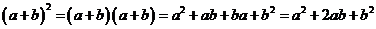
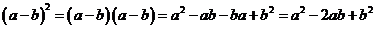
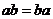( ,т.к. по определению произведения многочленов, операции над многочленами обладают свойствами коммутативности, ассоциативности и дистрибутивности.)

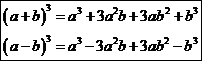
Доказательство:

.

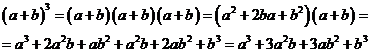
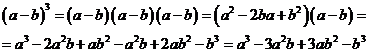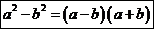
Доказательство:

.

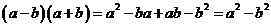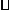
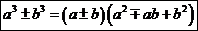
Доказательство:

.

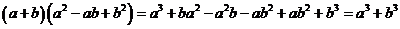
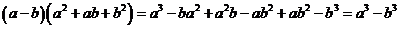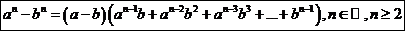
Доказательство:

Пусть 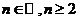, рассмотрим произведение

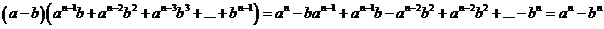
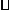
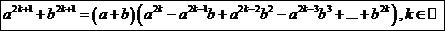
Доказательство:

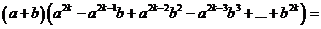
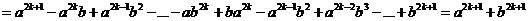
18. Свойства числовых неравенств.

О. Число 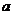больше числа 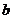, если разность 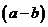– положительное число; число 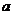меньше числа 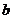, если разность 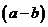– отрицательное число.

Теорема 1.

Если 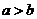, то 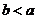; если 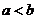, то .

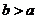Доказательство.

Если 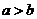, то по определению разность 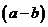– положительное число, тогда разность 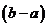- отрицательное число, а это значит, по определению, что 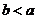. И наоборот.

Теорема 2.

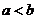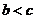Если и , то .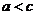

Доказательство.

По условию 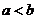и 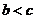, значит, по определению разность 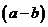– отрицательное число и разность 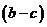– отрицательное число. Сумма отрицательных чисел – число отрицательное, поэтому сумма 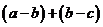– отрицательна. Преобразуем эту сумму 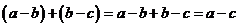. Следовательно, разность 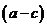– отрицательна и, по определению, .

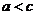Теорема 3.

Есл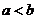и и 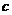– любое число, то .

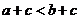Доказательство.

Преобразуем разность 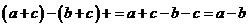. По условию, 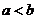, поэтому 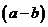– отрицательное число. Значит, и разность 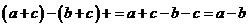- отрицательна. Следовательно, .

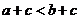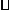
Теорема 4.

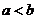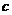Если и – положительное число, то ,

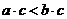Есл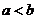и и 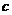– отрицательное число, то ,

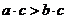Доказательство.

Преобразуем разность 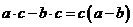. Так как 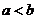, то разность 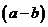– отрицательное число. Если 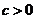, то произведение 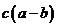– отрицательно, и, следовательно, 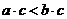. Если 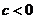, то произведение 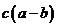– положительно, и, следовательно, .

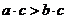Следствие.

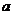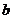Если и – положительные числа и 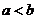, то .

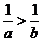Доказательство.

Разделим обе части неравенства 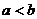на положительное число : .

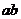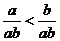Сократив дробь, получим, что 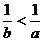, т.е. .

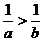Теорема 5.

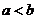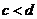Если и , то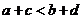

Доказательство.

Прибавим к обеим частям неравенства 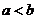число 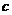, получим .

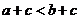Прибавим к обеим частям неравенства 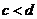число 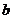, получим .

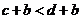Из неравенств 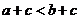и 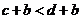,и теоремы 2 следует, что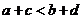

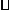
Теорема 6.

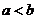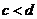Если и , где 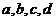– положительные числа, то .

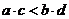Доказательство.

Умножим обе части неравенства 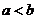на положительное число 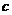, получим неравенство .

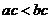Умножим обе части неравенства 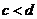на положительное число 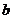, получим неравенство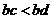

Из неравенств 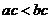и 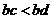и теоремы 2 следует, что .

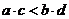19. Свойства числовых равенств.

Числовым равенством называется числовое выражение, содержащее знак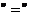

Свойство 1.

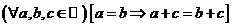
(если к обеим частям верного числового равенства прибавить одно и то же число, то получится также верное числовое равенство)

Свойство 2.

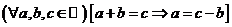
(если из одной части верного числового равенства перенести в другую часть слагаемое с противоположным знаком, то получится также верное числовое равенство)

Свойство 3.

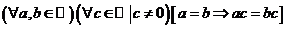
(если обе части верного числового равенства умножить на одно и то же число, то получится также верное числовое равенство)

Свойство 4.

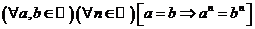
(если обе части верного числового равенства возвести в одну и ту же натуральную степень, то получится также верное числовое равенство)

20. Метод интервалов

О.Метод интервалов – метод решения рациональных неравенств.

Этот метод основан на следующей теореме математического анализа

(теореме Больцано-Коши), которую мы рассмотрим без доказательства:

Пусть функция 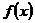на отрезке 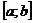и на концах его принимает разные по знаку значения,