Бросается 5 монет. Вероятность, что герб выпадет более трех раз равна

Бросается 5 монет. Вероятность, что герб выпадет более трех раз равна

Брошено 10 игральных костей. Предполагается, что все комбинации выпавших очков равновероятны. Укажите соответствие между событием и значением его вероятности:

выпала хотя бы одна «6» == 1-(5/6)¹⁰, выпало ровно три «6» == С³¹⁰(5/6)⁷(1/6)³, невыпало ни одной «6» == (5/6)¹⁰

Брошены две игральные кости. Вероятность того, что произведение выпавших очков равно 4, равно _______ (набрать число в виде десятичной дроби с тремя значащими цифрами)

0,0833

Брошены две игральные кости. Вероятность того, что сумма выпавших очков меньше 4, равно _____ (набрать число в виде десятичной дроби с тремя значащими цифрами)

0,0833

Брошены две монеты. Вероятность того, что выпадет и герб и решка, равна _____ (наберите десятичную дробь с точностью до одного знака)

0,5

В группе 30 студентов, из которых отлично учится 5 человек, хорошо – 18, удовлетворительно – 5 и слабо – 2. Преподаватель вызывает студента. Вероятность того, что вызванный студент или отличник или «хорошист», равна

23/30

В жилом доме 4000 ламп. Вероятность выключения лампы в вечернее время равна 0.5. Вероятность включения одновременно 2500 ламп можно вычислить, используя:

Локальную формулу Муавра-Лапласа

В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8, 9, 11, 12. Выборочная средняя результатов измерений, выборочная и исправленная дисперсии ошибок прибора равны соответственно

10; 2,5; 3,3

В магазин поступает товар с трех фабрик. Вероятности доставки товара в срок равны соответственно 0.6; 0.7; 0.5. Все партии не будут доставлены в срок с вероятностью:

В магазин поступает товар с трех фабрик. Вероятности доставки товара в срок равны соответственно 0.8; 0.7; 0.5. Хотя бы одна партия не будет доставлена в срок с вероятностью:

В таблице распределения случайной величиныС= (наберите десятичную дробь).

0,5

В таблице распределения случайной величиныС= (Наберите десятичную дробь).

0,4

В таблице статистического распределения, построенного по выборке, на одно число попала клякса .Это число

х = 0,2

В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво Эта цифра равна (наберите число).

В точке с абсциссой х = 0 точку перегиба имеют функции

у = , у =

В точке с абсциссой х = 0 точку экстремума имеют функции

y = 2x²+ 3,y = 4x⁴−4

В урне 3 белых и 7 черных шаров наугад вынимают два шара. Вероятность того, что оба шара черные, равна _______ (набрать число в виде десятичной дроби с тремя значащими цифрами)

0,467

В урне из 50 билетов 10 выигрышные. Вероятность того, что два вынутых билета выигрышные равна:

Верны ли определения?A) Величина уровня доверия влияет на величину доверительного интервала: чем больше уровень доверия, тем уже интервал.B) Доверительным интервалом с уровнем доверия – интервал, накрывающий значение оцениваемого параметра с вероятностью Подберите правильный ответ

А - нет, В - да

Верны ли определения?A) Величина уровня доверия влияет на величину доверительного интервала: чем больше уровень доверия, тем шире интервал.B) Доверительный интервал с уровнем доверия – интервал, накрывающий значение оцениваемого параметра с вероятностью .Подберите правильный ответ

А - да, В - да

Верны ли определения?A) геометрический смысл определенного интеграла -площадь криволинейной трапеции, ограниченной непрерывной кривойy=f(x), где на [a,b], численно равна определенному интегралу .B) Постоянный множитель можно выносить за знак интеграла Подберите правильный ответ

А - да, В - да

Верны ли определения?A) Двусторонний доверительный интервал с уровнем доверия для математического ожиданияaнормального распределения для случая, когда среднеквадратическое отклонение распределения неизвестно: B) Односторонний доверительный интервал с уровнем доверия для математического ожиданияaнормального распределения для случая, когда среднеквадратическое отклонение распределения неизвестно: Подберите правильный ответ

А - да, В - нет

Верны ли определения?A) Дисперсионный анализ – статистический метод, предназначенный для оценки влияния различных факторов на результат экспериментаB) Статистическая зависимость – такая зависимость между случайными величинами Х и Y, при которой изменение одной величины влечет изменение распределения другойПодберите правильный ответ

А - да, В - да

Верны ли определения?A) Дисперсия суммы двух случайных величин = .B) Если случайные величины и независимы, то дисперсия их разности = .Подберите правильный ответ

А - да, В - да

Верны ли определения?A) Для построения доверительного интервала для дисперсии надо пользоваться таблицами распределения Пирсона ( 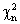)B) Для того, чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы распределения СтьюдентаПодберите правильный ответ

А - да, В - да

Верны ли определения?A) Для того, чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого известна, нужны таблицы распределения СтьюдентаB) Для построения доверительного интервала для дисперсии надо пользоваться таблицами нормального распределения.Подберите правильный ответ

А - нет, В - нет

Верны ли определения?A) Для того, чтобы построить доверительный интервал математического ожидания по выборке, когда дисперсия известна, необходимо определить выборочное среднее и выборочное среднеквадратическое sB) Для того, чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы распределения СтьюдентаПодберите правильный ответ

А - нет, В - да

Верны ли определения?A) Для того, чтобы построить доверительный интервал математического ожидания по выборке, когда дисперсия неизвестна, необходимо определить выборочное среднее и выборочное среднеквадратическое sB) Для построения доверительного интервала для дисперсии надо пользоваться таблицами нормального распределенияПодберите правильный ответ

А - да, В - нет

Верны ли определения?A) Если случайные величины независимы, то коэффициент корреляции равен нулю.B) Если коэффициент корреляции равен нулю, то случайные величины независимы.Подберите правильный ответ

А - да, В - нет

Верны ли определения?A) Критическая область – область, при попадании в которую значения статистики критерия, сосчитанной по выборке, основная гипотеза отвергаетсяB) Критические значения-точки, разделяющиекритическую область и область допустимых значенийПодберите правильный ответ

А - да, В - да

Верны ли определения?A) Линейная регрессия имеет место, если функция регрессии – линейная функция, т.е. ее можно представить в виде уравнения y = f(x) = αx + βB) Функция регрессии Х на Y - условное математическое ожидание M(Y/Х = x) как функция от х: M(Y/Х = x) = f(x)Подберите правильный ответ

А - да, В - нет

Верны ли определения?A) Мощностью критерияназывается вероятность (1– ) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу Н⁰, когда она вернаB) Уровень значимости – вероятность α попадания в критическую область в случае, если основная гипотеза истиннаПодберите правильный ответ

А - нет, В - да

Верны ли определения?A) Мощностью критерияназывается вероятность (1– ) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу Н⁰, когда она невернаB) Ошибка первого рода – ошибка α, которую совершают, отвергнув основную гипотезу, когда она истиннаПодберите правильный ответ

А - да, В - да

Верны ли определения?A) Несобственный интеграл от непрерывной функции на всей прямой определяется равенством: ,B) Для вычисления определенного интеграла применяется формула Ньютона-Лейбница: , гдеF(x) – одна из первообразныхf(x)Подберите правильный ответ

А - да, В - да

Верны ли определения?A) Определенный интеграл Римана от функцииf(x) на отрезке [a,b]- предел интегральных сумм при условии , обозначаемый .B) Аддитивность определенного интеграла – свойство, состоящее в том, что = + для любого .Подберите правильный ответ

А - да, В - да

Верны ли определения?A) Ошибка первого рода – ошибка α, которую совершают, отвергнув основную гипотезу, когда она истиннаB) Ошибка второго рода – ошибка β, которую совершают, приняв основную гипотезу, когда она ложнаПодберите правильный ответ

А - да, В - да

Верны ли определения?A) Ошибка первого рода – ошибка β, которую совершают, приняв основную гипотезу, когда она ложнаB) Ошибка второго рода – ошибка α, которую совершают, отвергнув основную гипотезу, когда она истиннаПодберите правильный ответ

А - нет, В - нет

Верны ли определения?A) При проверке гипотезы о виде распределения, когда параметры его неизвестны, применяется критерий χ²с заменой неизвестных параметров на эмпирические значения и уменьшается число степеней свободыB) При проверке гипотез о численном значении дисперсии (σ = σ⁰) при неизвестном среднем а используется статистика , имеющая распределение χ^2n-1Подберите правильный ответ

А - да, В - да

Верны ли определения?A) При проверке с помощью критерия χ²гипотезы о равномерном распределении R(a,b), когда концы интервала a и b неизвестны, а число интервалов группировки равно m, статистика χ²имеет распределение χ²с числом степеней свободы m – 3B) При проверке с помощью критерия χ²гипотезы о равномерном распределении R(a,b), когда концы интервала a и b известны, а число интервалов группировки равно m, статистика χ²имеет распределение χ²с числом степеней свободы m – 2Подберите правильный ответ

А - да, В - нет

Верны ли определения?A) Распределение вероятностей, которое имеет случайная величина , где и – независимые случайные величины, распределенные по 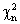с n¹и n²степенями свободы, называется распределением Фишера-Снедекора, оно определяется двумя параметрами – n¹и n²B) Статистика F, использующаяся в процедуре проверки равенства дисперсий двух генеральных совокупностей, имеет распределение СтьюдентаПодберите правильный ответ

А - да, В - нет

Верны ли определения?A) Регрессионная модель - модель, в которой один из двух признаков изучаемой двумерной величины, например x, выступает в качестве независимой компоненты (чаще всего это время), т.е. переменная x вообще не случайна, а случайна только переменная yB) Функция регрессии Y на Х - условное математическое ожидание M(Y/Х = x) как функция от х: M(Y/Х = x) = f(x)Подберите правильный ответ

А - да, В - да

Верны ли определения?A) Случайные величины, имеющие нулевой коэффициент, называют некоррелированными.B) Некоррелированные случайные величины не зависимы.Подберите правильный ответ

А - да, В - да

Верны ли определения?A) Случайным вектором или n-мерной случайной величиной называют упорядоченный набор из n случайных величин 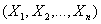B) Непрерывный случайный вектор – этослучайный вектор, компоненты которого непрерывные случайные величиныПодберите правильный ответ

А - да, В - да

Верны ли определения?A) Статистика F, использующаяся в процедуре проверки равенства дисперсий двух генеральных совокупностей, имеет распределение Фишера-СнедекораB) Для проверки гипотезы о виде распределения применяется статистика , имеющая распределение χ², число степеней которого равно m – 2 (число заменяемых параметров равно 2)Подберите правильный ответ

А - да, В - нет

Верны ли определения?A) Статистика, с помощью которой по эмпирическому значению коэффициента корреляции r и числу испытаний n проверяется значимость коэффициента корреляции, вычисляется по формуле B) Статистика, с помощью которой по эмпирическому значению коэффициента корреляции r и числу испытаний n проверяется значимость коэффициента корреляции, имеет распределение Фишера-СнедекораПодберите правильный ответ

А - да, В - нет

Верны ли определения?A) Статистическая зависимость - такая зависимость между случайными величинами Х и Y, при которой изменение одной величины не влечет изменение распределения другойB) Корреляционная статистическая зависимость - такая зависимость, в которой при изменении одной величины изменяется среднее значение (математическое ожидание) другойПодберите правильный ответ

А - нет, В - да

Верны ли определения?A) Точность интервальной оценки определяется доверительной вероятностьюB) Надежность интервальной оценки определяется центром доверительного интервалаПодберите правильный ответ

А - нет, В - нет

Верны ли определения?A) Уровень значимости – вероятность α попадания в критическую область в случае, если основная гипотеза истиннаB) Критическая область – область, при попадании в которую значения статистики критерия, сосчитанной по выборке, основная гипотеза принимаетсяПодберите правильный ответ

А - да, В - нет

Верны ли определения?A) Условная функция распределения случайной величины при условии равна B) Случайные величины и называют независимыми, если функция распределения вектор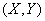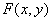а равна Подберите правильный ответ

А - да, В - нет

Верны ли определения?A). Величина коэффициента корреляции заключена в пределах B) Для независимых случайных величин ковариация равна нулю.Подберите правильный ответ

А - нет, В - да

Верны ли определения?A). вероятность попадания случайной величины на заданный интервал выражается через плотность распределения .B) интервал практически возможных значений нормально распределенной случайной величины равен ( , где m, – параметры нормального распределения.Подберите правильный ответ

А - да, В - да

Верны ли определения?A). Математическое ожидание случайной величины, имеющей показательное распределение с параметром : B) Математическое ожидание случайной величины, имеющей равномерное распределение на отрезке [a, b]:MX= Подберите правильный ответ

А - да, В - нет

Верны ли определения?A). Плотность распределения и функция распределения двумерной случайной величины связаны соотношением B) Закон распределения дискретного случайного вектора 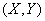– это совокупность всех возможных значений данного вектора и вероятностей 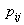, равных 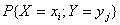Подберите правильный ответ

А - да, В - да

Верны ли определения?A). Плотность распределения случайной величины, равномерно распределенной на [a,b], имеет вид: ^.B) Непрерывная случайная величина Х имеет нормальное распределение с параметрами m и , если ее плотность распределения имеет вид .Подберите правильный ответ

А - нет, В - да

Верны ли определения?A). Случайная величина Х распределена равномерно на отрезке (a, b), если ее плотность постоянна и равна .B) Непрерывная случайная величина Х, принимающая неотрицательные значения, имеет показательное (экспоненциальное) распределение с параметром , если плотность распределения имеет вид ^.Подберите правильный ответ

А - да, В - да

Верны ли определения?A). Функция распределения случайной величины, равномерно распределенной на [a,b], имеет вид: ^.B) Непрерывная случайная величина Х, принимающая неотрицательные значения, имеет показательное (экспоненциальное) распределение с параметром , если функция распределения имеет вид: ^.Подберите правильный ответ

А - да, В - нет

Верны ли определения?А) Геометрический смысл дифференциала функции – дифференциал функцииy=f(x) в точкеx⁰равен приращению ординаты касательной приx→x⁰.B) График дифференцируемой функции называется выпуклым в интервале (a,b), если он расположен ниже любой своей касательной в этом интервале.Подберите правильный ответ

А - да, В - нет

Верны ли определения?А) Дифференциал функцииy=f(x) в точкеx⁰– произведение производной функцииf′(x⁰) на приращение аргумента ∆x.B) Если функцияy=f(x) возрастает на интервале (a,b), тоf′(x) >0 на этом интервале.Подберите правильный ответ

А - да, В - да

Верны ли определения?А) Для проверки гипотезы о виде распределения применяется статистика , имеющая распределение χ², число степеней которого равноm– r – 1, где m – число слагаемых, а r – число параметров распределения, замененных на эмпирические значенияВ) При проверке гипотезы об однородности m выборок при m>2 в качестве теоретических частот используются эмпирические частоты, полученные при объединении всех выборокПодберите правильный ответ

А - да, В - да

Верны ли определения?А) Достаточный признак существования экстремума функцииy=f(x):f¢¢(x) = 0.B) Точка максимума функцииy=f(x) – точкаx⁰, для которой существует такая окрестность точкиx⁰, что для всехx≠x⁰, принадлежащих этой окрестности, выполняется неравенствоf(x⁰) >f(x).Подберите правильный ответ

А - нет, В - да

Верны ли определения?А) Достаточный признак существования экстремума функцииy=f(x):f¢¢(x) = 0.B) Точка максимума функцииy=f(x) – точкаx⁰, для которой существует такая окрестность точкиx⁰, что для всехx≠x⁰, принадлежащих этой окрестности, выполняется неравенствоf(x⁰) >f(x).Подберите правильный ответ

А - нет, В - да

Верны ли определения?А) Если и – две переменные величины, причем , , то есть .B) Переменная величина является бесконечно малой (б.м.), если , т.е. для , начиная с некоторого момента в изменении выполняется неравенство .Подберите правильный ответ

А - нет, В - да

Верны ли определения?А) Если функцияy=f(x) убывает на интервале (a,b), тоf′(x) >0 на этом интервалеB) График дифференцируемой функции называется вогнутым в интервале (a,b), если он расположен ниже любой своей касательно в этом интервале.Подберите правильный ответ

А - нет, В - да

Верны ли определения?А) Задана числовая последовательность, если каждому натуральному числу 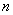по некоторому закону поставлено в соответствие определенное действительное число .B) С помощью логических символов определение предела последовательности выражается .Подберите правильный ответ

А - да, В - нет

Верны ли определения?А) Надежность интервальной оценки определяется доверительной вероятностьюB) Точность интервальной оценки определяется длиной доверительного интервалаПодберите правильный ответ

А - да, В - да

Верны ли определения?А) Неопределенный интеграл функцииy=f(x) – совокупность всех первообразных: ∫f(x)dx=F(x) +C.B) Первообразная функция от данной функцииf(x) – функцияF(x), производная которой равнаf(x).

А - да, В - да

Верны ли определения?А) Постоянный множитель можно выносить за знак интеграла.B) Формула интегрирования по частям .

А - да, В - нет

Верны ли определения?А) Свойство определенного интеграла: .B) Несобственный интеграл сходится, если существует конечный предел .

А - нет, В - да

Верны ли определения?А) ТочкаM⁰(x⁰,y⁰), лежащая на графике и отделяющая выпуклую часть графика от вогнутой, называется точкой перегиба функцииy=f(x).B) Если вторая производная функцииy=f(x) равна нулю в точкеx⁰, тоx⁰– точка перегиба.Подберите правильный ответ

А - да, В - нет

Верны ли определения?А) Функцией называется отображение числового множестваXв числовое множествоY.B) Областью определения функции называют множествоY.Подберите правильный ответ

А - да, В - нет

Верны ли определения?А) Функцией распределения двумерной случайной величины 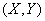называют функцию двух переменных 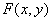, равную 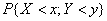В) Плотность распределения и функция распределения двумерной случайной величины связаны соотношением Подберите правильный ответ

А - да, В - нет

Верны ли утверждения?A) Дана выборка объема n: х¹, х², х³, …, хⁿ. Выборочное среднее находится по формуле: B) Дана выборка объема n: х¹, х², х³, …, хⁿ. Выборочная дисперсия находится по формуле:

А - да, В - да

Верны ли утверждения?А) Вариационным рядом для выборки объема n = 7: 3, 5, -2, 1, 0, 4, 3 является ряд –2, 0, 1, 3, 3, 4, 5В) Вариационным рядом для выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12 является ряд – 0, -2, 3, 3, 4, 5, 9, 11, 12Подберите правильный ответ

А - да, В - нет

Верны ли утверждения?А) Вариационным рядом для выборки объема n = 8: 3, 2, -2, 1, 0, 2, 4, 3 является ряд 0, 1, -2, 2, 3, 4В) Вариационным рядом для выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 4, 12 является ряд -2, 0, 3, 3, 4, 4, 5, 9, 12Подберите правильный ответ

А - нет, В - да

Верны ли утверждения?А) Дан вариационный ряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 9, 11, 12, выборочная медиана для этого ряда – d равна 4.В) Дан вариационный ряд выборки объема n = 8: –2, 0, 1, 3, 4, 4, 5, 8, выборочная медиана для этого ряда – d равна 3.Подберите правильный ответ

А - нет, В - нет

Верны ли утверждения?А) Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12, выборочная медиана для этого ряда – d равна 4.В) Дан вариационный ряд выборки объема n = 7: –2, 0, 1, 3, 3, 4, 5, выборочная медиана для этого ряда – d равна 3.Подберите правильный ответ

А - да, В - да

Верны ли утверждения?А) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее возрастет в 25 раз.В) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки увеличить на 10 , то выборочное среднее возрастет на 10.Подберите правильный ответ

А - нет, В - да

Верны ли утверждения?А) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки увеличить в 9 раз, то выборочное среднее возрастет в 9 раз.В) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки увеличить на 5 , то выборочное среднее возрастет на 25.Подберите правильный ответ

А - да, В - нет

Верны ли утверждения?А) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки уменьшить в 3 раза, то выборочное среднее уменьшится в 3 раза.В) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки увеличить в 3 раза, то выборочная дисперсияS²возрастет в 9 раз.Подберите правильный ответ

А - да, В - да

Верны ли утверждения?А) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки уменьшить на 10, то выборочное среднее не изменится.В) Дана выборка объема n: х¹, х², …, хⁿ. Если каждый элемент выборки увеличить на 10, то выборочная дисперсияS²не изменится.Подберите правильный ответ

А - нет, В - да

Верны ли утверждения?А) Для того чтобы в 5 раз сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в 25 раз.В) Для того чтобы в вдвое расширить доверительный интервал, построенный для математического ожидания, число наблюдений надо уменьшить в 4 раза.

А - да, В - да

Верны ли утверждения?А) Для того чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в 4 разаВ) Для того чтобы вдвое расширить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в 2 раза.

А - да, В - нет

Верны ли утверждения?А) Для того чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо уменьшить вдвое.В) Для того чтобы втрое расширить доверительный интервал, построенный для математического ожидания, число наблюдений надо уменьшить в 9 раз.

А - нет, В - да

Верны ли утверждения?А) Размах вариационного ряда для выборки объема n = 7: 5, 2, -3, 1, 0, 2, 4, 3 равен 5.В) Размах вариационного ряда для выборки объема n = 9: 0,-2,-3, 3, 4, 5, 9, 4, 12 равен 12.Подберите правильный ответ

А - нет, В - нет

Верны ли утверждения?А) Размах вариационного ряда для выборки объема n = 8: 3, 2, -2, 1, 0, 2, 4, 3 равен 6.В) Размах вариационного ряда для выборки объема n = 9: 0,-2, 3, 3, 4, 5, 9, 4, 12 равен 14.Подберите правильный ответ

А - да, В - да

Верными являются высказывания:А) Вероятность попадания непрерывной случайной величины в интервал (a, b), выражается через функцию распределения следующей формулойP(a<>X<>b) =F(b) –F(a)В) Плотность распределения непрерывной случайной величины являетсянеотрицательной

A- да,B- да

Верными являются высказывания:А) Вероятность попадания случайной величины в интервал (a, b) выражена через плотность распределения следующей формулойP(a<>X<>b) =f(b) –f(a)В) Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образомF(x) = (x)dx

A- нет,B- нет

Верными являются высказывания:А) Вероятность суммы двух случайных событий вычисляется по формуле Р(А+В) = Р(А) + Р(В)В) Условную вероятность события А при условии, что произошло событие В можно вычислить по формуле: Р(А )=

A- нет,B- да

Верными являются высказывания:А) Два события будут несовместными, если Р(АВ) = 0В) Два события будут совместными, если Р(АВ) = 1

A- да,B- нет

Верными являются высказывания:А) Если события А и В несовместны, то для них справедливо равенство Р(А + В) = Р(А) + Р(В)В) Два события А и В называются независимыми, если Р(А В) = Р(А) Р(В)

A- да,B- да

Верными являются высказывания:А) Математическое ожидание дискретной случайной величины равно В) Математическое ожидание суммы случайной величины Х и постоянной С равноM(X+C) =MX

A- да,B- нет

Верными являются высказывания:А) Нормальное распределение имеет вид 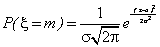В) Распределение Пуассона имеет вид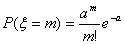

A- да,B- да

Верными являются высказывания:А) Случайной величиной называется переменная величина,которая определяется совокупностью возможных значенийВ) Пределы функции распределения F(x) на плюс и минус бесконечности равны соответственно F 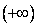= 1, F =

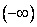A- нет,B- нет

Верными являются высказывания:А) Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле В) Среднеквадратическое отклонение непрерывной случайной величины вычисляется по формуле

A- нет,B- да

Верными являются высказывания:А) Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле 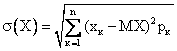В) Среднеквадратическое отклонение непрерывной случайной величины вычисляется по формуле

A- да,B- нет

Верными являются высказывания:А) Формула Бейеса имеет вид В) Если события А, В, С независимы, то Р(А + В + С) = Р(А) Р(В) Р(С)

A- нет,B- нет

Верными являются высказывания:А) Формула Бейеса имеет вид В) Если события А, В, С независимы, то Р(А + В + С) = Р(А) Р(В) Р(С)

A- нет,B- нет

Верными являются высказывания:А) Формула полной вероятности имеет вид В) Формула Бейеса имеет вид

A- да,B- да

Верными являются высказывания:А) Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образомF(x) = 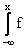(x)dxВ) Вероятность попадания случайной величины в интервал (a, b) выражена через плотность распределения следующей формулойP (a (x) dx

A- да,B- да

Верными являются высказывания:А) Функция распределения случайной величины не убываетВ) Функция распределения дискретной случайной величины разрывная, ступенчатая

A- да,B- да

Выпущено 100 лотерейных билетов, причем установлены призы, из которых восемь выигрышей по 1 руб, два-по 5 руб., один – 10 руб.Установите соответствие между левыми и правыми частями таблицы ( с точностью до 0,01)

p⁰- билет не выиграл == 0,89, p¹- билет выиграл 1 руб. == 0,08, p¹⁰- билет выиграл 10 руб. == 0,01, p⁵- билет выиграл 5 руб. == 0,02

Два стрелка стреляют по разу в общую мишень. Вероятность попадания в цель у одного стрелка 0,8; у другого 0,6. Установите соответствие между вероятностями и их значениями. Установите соответствие между левыми и правыми частями таблицы

Цель не поражена == 0,08, Цель поражена двумя пулями == 0,48, Цель поражена хотя бы одной пулей == 0,92

Корректура книги объемом в 500 страниц имеет 500 ошибок. Число опечаток на одной странице – случайная величина, распределенная по закону Пуассона. Вероятность того, что на случайно выбранной странице окажется 2 опечатки, равна

Случайная величина Х распределена