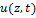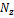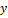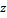Колебания упругих тел с распределенными параметрами.

Перемещения, деформации, внутренние силы и моменты, распределение массы в реальных телах и их моделях описываются функциями положения (места) и времени, поэтому число степеней свободы бесконечно. Однако в зависимости от требуемой точности и характера изучаемого движения (покоя) можно свести задачу к модели с несколькими степенями свободы (осуществить дискретизацию). Имеются различные способы дискретизации.

Метод Рэлея-Ритца

Для иллюстрации метода рассмотрим прямолинейный стержень, который может совершать продольные, крутильные, изгибные колебания. Перемещения задаются в виде ряда

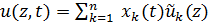, (1)

где 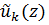- задаваемые линейно-независимые функции координат, (координатные функции), а 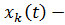неизвестные функции времени, которые в терминах механики Лагранжа можно назвать обобщенными координатами. Если используется только одна координатная функция, метод называется методом Рэлея. Координатные функции должны, по меньшей мере, удовлетворять краевым условиям для перемещений (т.н. кинематическим условиям); разумеется, если удовлетворяются хотя бы некоторые силовые условия, результаты будут ближе к точному решению.

Кинетическая и потенциальная энергии деформации (внутренняя энергия) во всех отдельно рассматриваемых случаях имеют вид

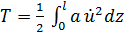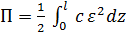, , (2)

где 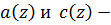приведенные в таблице коэффициенты инерции и жесткости, а 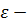деформация. Подставляя (1) в (2), получим

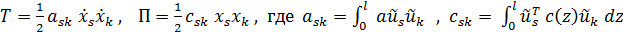
Уравнения Лагранжа для полученной системы с 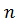степенями свободы имеют вид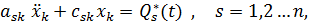

где 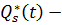обобщенные силы, соответствующие внешним воздействиям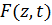

.

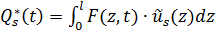	Переме щение	Деформация	Жесткость	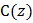Инерция	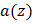Усилия и Моменты
Продольные колебания		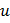		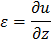	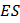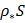Продольная сила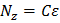
Изгибные колебания 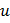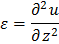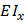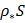x					Перерезывающая сила 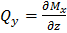Изгибающий момент

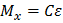Пример 1. Свободные изгибные колебания консольного клина переменного круглого сечения

Кинетическая энергия 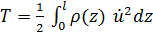, где 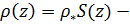масса единицы длины стержня (погонная масса), 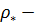трехмерная плотность, 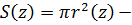площадь сечения, 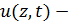проекция на ось 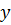перемещений точек оси стержня.

z

y

x

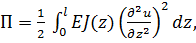Потенциальная энергия где 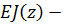изгибная жесткость, 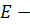модуль Юнга, 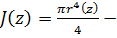момент инерции сечения относительно оси X. Введя безразмерные перемещение 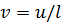и координату 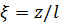, будем иметь ,

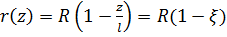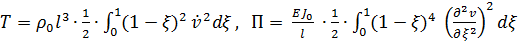, (1)

.

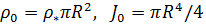Полагая в методе Рэлея 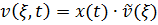, где функция 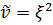при 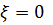удовлетворяет условиям жесткой заделки 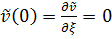, получим

.

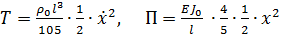Уравнение колебаний имеет вид

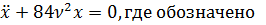
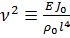. Таким образом, частота колебаний

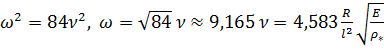
Этот результат на 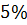отличается от приведенного в [9] точного, полученного Кирхгофом значения 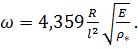(2)

Для уточнения полученного результата положим 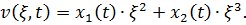Подставляя это представление в (1), получим

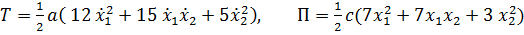, где обозначено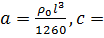 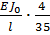. Отношение 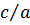обозначим для удобства .

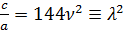Уравнения Лагранжа имеют вид

.

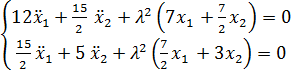Отыскивая решение в виде 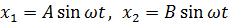, получим частотное уравнение

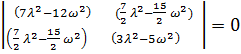или 15 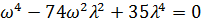, откуда

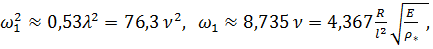(3)

что только на 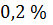превышает точное значение (2).