Постоянный тензор инерции. Осевые и центробежные моменты инерции. Вычисление моментов инерции относительно произвольных осей.

Из определения тензора инерции 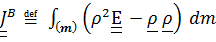, вычисляемого в актуальном положении твердого тела, ясно, что тензор инерции зависит от времени. Разложим вектор и единичный тензор по базису , жестко связанному с телом: .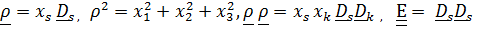

Тогда тензор инерции примет вид 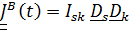, где координаты 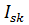постоянные, a переменные 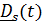и 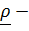это повернутые вместе с телом постоянные векторы 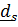и 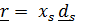в отсчетном ( например, при t=0) положении. Таким образом, 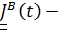это повернутый вместе с телом («вмороженный» в тело) постоянный тензор инерции

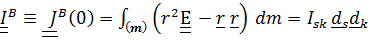. (5.20)

Последнее предложение с помощью тензора поворота «переводится» в формулу

B

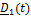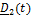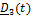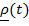B

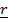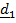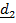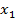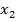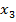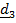dm

.

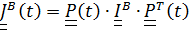Далее мы будем говорить о постоянном тензоре 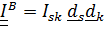, координаты которого называются моментами инерции.

Из (5.20) ясно, что тензор инерции симметричный 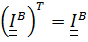, т.е. .

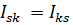Формально координаты 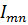тензора в ортонормированном базисе вычисляются с помощью скалярного умножения тензора слева на 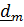, а справа на :

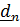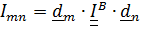. (5.21)

Из (5.20) имеем:

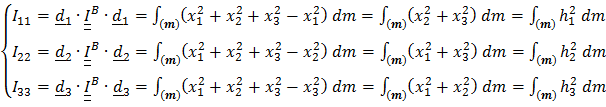, (5.22)

где 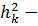квадрат расстояния от элемента 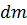до «К»- ой оси,

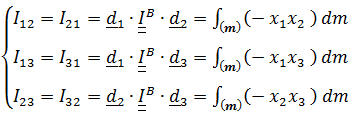(5.23)

Моменты инерции (5.22) называются осевыми, а(5.23) - центробежными.

Из (5.22) следуют своеобразные «правила треугольника»

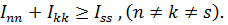
Например, ,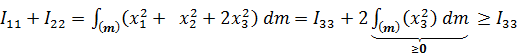

причем ясно, что равенство возможно только в тех случаях, когда у всех точек тела координата 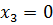; например, если тело – бесконечно тонкий стержень или бесконечно тонкая пластина.

5.2.3. Зависимость тензора инерции от точки (обобщенная теорема Гюйгенса- Штейнера).

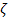B ·

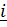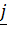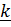z

y

x

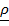· C

dm

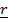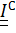Для описания движения твердых тел необходимо вычислять тензор инерции относительно разных точек. Так, например, тело может вращаться вокруг различных неподвижных точек и, соответственно, осей. Чтобы избавиться от необходимости каждый раз вычислять интегралы (5.25), (5.26), найдем связь между центральным тензором инерции ,который является неотъемлемым, вычисленным или измеренным атрибутом тела, и тензором инерции в некоторой точке .

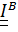Подставляя в определение тензора 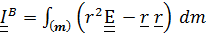выражения

,

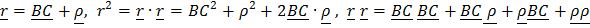получим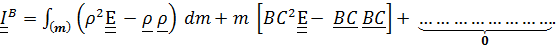

Все невыписанные слагаемые равны нулю, поскольку они содержат равный нулю множитель 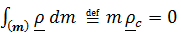(постоянные вектор 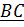и тензор 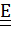выносятся из интегралов). Таким образом, получили обобщенную теорему Гюйгенса- Штейнера

. (5.24)

Пусть 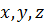- оси с началом в точке В и базисными векторами 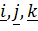, а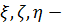

параллельные им оси с началом в центре масс (центральные оси) c координатами .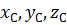

Умножая (5.24) слева и справа скалярно на 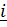, получим формулу связи для осевых моментов инерции

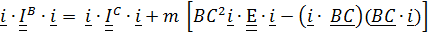или

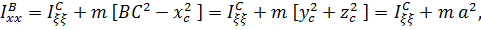(5.25)

где 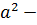квадрат расстояния между осями X и .

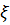Умножая (5.24) слева на 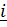и справа на 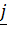, получим формулу связи для центробежных моментов инерции

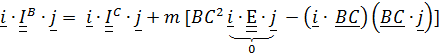или

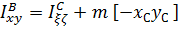. (5.26)

Разумеется, формулы (5.25) и (5.26) легко записываются и для других осей.

Заметим также, что поскольку осевые моменты инерции не зависят от положения точек на осях, часто в формулах (5.25) «имена» точек В и С опускаются.

Из (5.25) следует, что осевые моменты инерции минимальны, если оси центральные (вспомним о центре масс, как о точке, «ближайшей» ко всем точкам тела).