Глава 5. Фундаментальные законы механики.

Фундаментальные законы формулируются в инерциальных системах отсчета.

Инерциальная система отсчета - система, относительно которой изолированная от внешних сил (одинокая во всем мире) материальная точка либо движется равномерно и прямолинейно, либо находится в покое.

Заметим, что этим определением вводится понятие равномерного течения времени итем самым способ тарировки часов.

Подробное изложение рассматриваемых вопросов можно найти в книге [5].

Первый фундаментальный закон механики - закон баланса количества движения. Открытые и закрытые тела.

Скорость изменения количества движения тела равна главному вектору внешних сил плюс скорость подвода количества движения в тело.

(5.1)

Количество движения (импульс) одной точки ;

тела, состоящего из материальных точек ; (5.2)

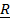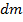тела, занимающего какую-либо область в пространстве с непрерывно распределенной массой (континуального тела)

. (5.3)

Скорость подвода количества движения в тело определяется как

, (5.4)

где – присоединяющаяся к телу за время со скоростью масса.

Тела, обменивающиеся массой со своим окружением, называются открытыми, не обменивающимися – закрытыми. Примером открытого тела является, например рабочее колесо турбины вместе с рабочим телом (газ, пар, вода), участок речного русла или трубопровода, ракета. Для закрытых тел, разумеется .

Введение открытых тел - вынужденная мера в механике, поскольку нас обычно интересует, что сейчас происходит в данном месте пространства, а проследить за историей каждой частицы жидкости, оказавшейся в выделенном теле, практически невозможно; частица «приходит неизвестно откуда и уходит неизвестно куда».

Для материальной точки первый ФЗМ принимает вид второго закона Ньютона

(5.5)

Пример. Уравнение Мещерского. Формула Циолковского.

x

В качестве примера применения первого закона для открытых тел рассмотрим ракету массой где «сухая» масса ракеты, масса топлива в ракете. Заметим, что описать движение закрытого тела постоянной массы – ракеты с уже сгоревшим топливом (газом) практически невозможно, поскольку это потребовало бы задания сил, действующих не только на ракету, но и на сгоревшее топливо .

Запишем уравнение первого фундаментального закона

.

Количество движения . В главный вектор внешних сил входят сила тяжести, аэродинамические силы и, строго говоря, давление на срезе сопла двигателя.

Скорость подвода количества движения

где масса отделяющегося за время газа , его скорость, а знак (-1) учитывает факт именно отделения.

Поскольку то Таким образом, , откуда

. (1)

Это уравнение было получено И.В. Мещерским в 1897 г.

В терминах кинематики относительного движения скорость (абсолютная) отделяющегося газа равна сумме переносной скорости ракеты и относительной скорости , поэтому уравнение принимает вид

(

или, если ввести так называеьую реактивную силу , .

Предположим, что ракета движется поступательно и что относительная скорость истечения постоянна. Проецируя ( на ось Х, получим с учетом : . Отсюда, интегрируя

Скорость ракеты, израсходовавшей все топливо, равна

Эту формулу опубликовал К.Э. Циолковский в 1903 г.