Матрица поворота. Матрица спина. Вектор угловой скорости.

Запишем очевидную векторную формулу для вектора положения 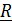какой-либо точки 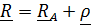(рис.4.6) в матричном виде. Найдем координаты вектора 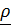относительно отсчетного базиса. Разложим вектор 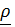по актуальному базису 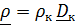и введем «перенесенный» вектор 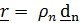, координаты которого в отсчетном базисе равны координатам вектора 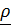в актуальном; иными словами, 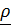- «повернутый» вместе с телом вектор 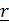(Рис.4.6).

Рис. 4.6.

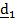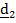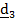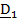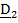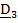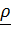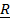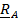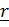Раскладывая векторы 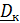по отсчетному базису ,получим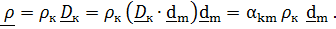

Введем матрицу поворота и столбцы ,

.

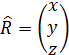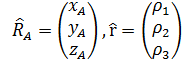Векторная формула 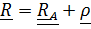в матричной записи имеет вид

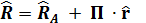(4.14)

1. Матрица поворота 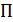является ортогональной, т.е.

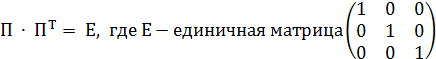. (4.15)

Доказательство этого утверждения – формула (4.9)

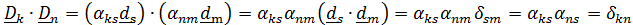
Вычисляя определитель произведения (4.15), получим 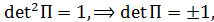а так как в отсчетном положении 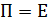, то 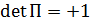(ортогональные матрицы с определителем, равным (+1), называют собственно ортогональными или матрицами поворота). Матрица поворота при умножении на векторы не изменяет ни длин векторов, ни углов между ними, т.е. действительно их поворачивает.

2. Матрица поворота имеет один собственный (неподвижный) вектор 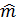, который задает ось поворота. Иными словами, надо показать, что система уравнений 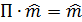, где 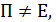имеет единственное решение. Запишем систему в виде ( 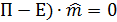. Определитель этой однородной системы равен нулю, так как

,

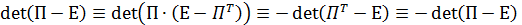следовательно, система имеет ненулевое решение. Предположив, что имеется два решения 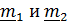, тут же придем к выводу, что перпендикулярный к ним 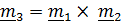также является решением (углы между векторами не изменяются), а это значит, что 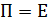т.е. поворота нет..

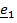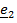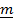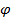Рис.4.7

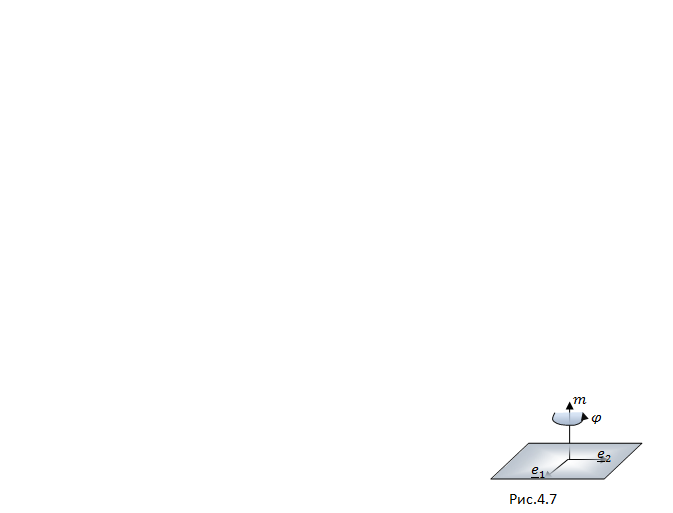В дальнейшем будем считать неподвижный вектор оси поворота 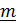единичным, а положительное направление отсчета угла поворота 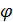согласованным с направлением 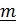в соответствии с принятой ориентацией пространства (т.е. с конца 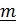положительный поворот виден против часовой стрелки) (рис.4.7). Матрицу поворота будем обозначать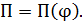

Матрица 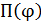в ортонормированном базисе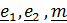

имеет вид .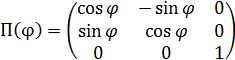

2. Дифференцируя (4.15), получим 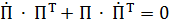или, обозначив 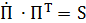– матрица сп 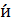на (англ. to spin - вертеть) 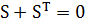.Таким образом, матрица спина кососимметрическая: 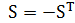. Умножая справ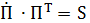а на 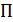, получим формулу Пуассона для матрицы поворота:

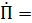
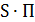(4.16)

Мы подошли к самому трудному в рамках матричного описания моменту – определению вектора угловой скорости.

Можно, разумеется, поступить стандартным (см., например, 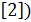способом и написать: « введем обозначения для элементов кососимметрической матрицы S по формуле

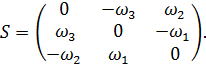
Если составить вектор 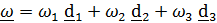, то результат умножения матрицы 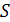на вектор 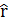может быть представлен в виде векторного произведения 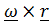». В приведенной цитате 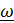- вектор угловой скорости.

Дифференцируя (4.14), получим матричную запись основной формулы кинематики твердого тела :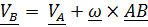

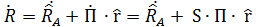(4.17)

Матричный подход, будучи удобным для вычислений, очень мало подходит для анализа и вывода соотношений; всякую формулу, написанную на векторном и тензорном языке, без труда можно записать в матричном виде, а вот получить компактную и выразительную формулу для описания какого-либо физического явления в матричном виде трудно.

Кроме того, не следует забывать, что элементы матрицы являются координатами (компонентами) тензора в каком-либо базисе. Сам тензор не зависит от выбора базиса, а его компоненты зависят. Для безошибочной записи в матричном виде необходимо, чтобы все векторы и тензоры, входящие в выражение, были записаны в одном базисе, а это не всегда удобно, поскольку разные тензоры имеют «простой» вид в разных базисах, поэтому нужно пересчитывать матрицы с помощью матриц перехода.