Допускающие понижение порядка

Одним из основных методов решения уравнений высших порядков является понижение порядка уравнения, т.е. сведение его с помощью соответствующей замены к дифференциальному уравнению более низкого порядка.

Рассмотрим некоторые типы уравнений, допускающих понижение порядка.

I тип. Уравнение вида .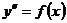

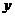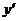Заметим, что уравнение не содержит и . Уравнения этого вида решаются двукратным интегрированием. Введем новую функцию 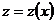, полагая 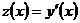. Тогда 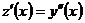, и уравнение превращается в уравнение первого порядка: .

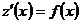Решая его, находим, что 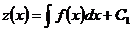. Так как 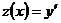, то .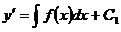

Интегрируя еще раз, получаем искомое решение:

,

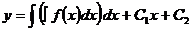где 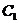и 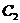- произвольные постоянные.

Пример 2Найти общее решение уравнения

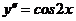
Решение: Положим 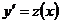; тогда .

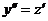Получаем уравнение первого порядка 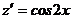. Интегрируя его, найдем 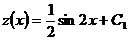или .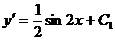

Интегрируя второй раз, находим искомое общее решение:

,

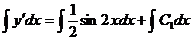т.е. .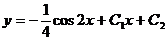

Замечание

Аналогичным способом решение уравнения вида 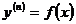находится методом 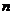- кратного интегрирования.

II тип. Уравнение вида 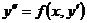, т.е. уравнение не содержит явным образом .

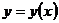Положим, как и в предыдущем случае, 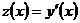. Тогда 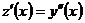, и уравнение преобразуется в уравнение первого порядка 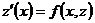относительно неизвестной функции 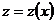. Решая его, находим общее решение .

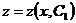Так как 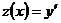, то имеем уравнение 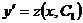. Отсюда, интегрируя еще раз, получаем искомое решение ,

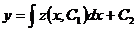где 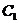и 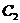- произвольные постоянные.

Пример 3Найти общее решение уравнения .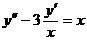

Решение: Полагая 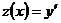, получаем линейное уравнение первого порядка 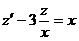. Решаем его с помощью подстановки Бернулли :

.

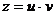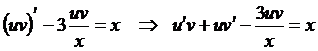
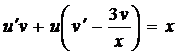Отсюда имеем: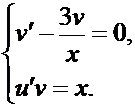

Решаем сначала первое уравнение системы:

.

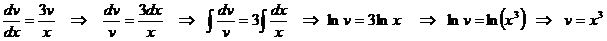Подставляя 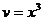во второе уравнение системы, получим:

.

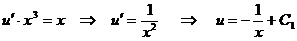Следовательно, 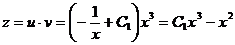. Тогда .

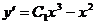Интегрируя еще раз, находим искомое общее решение: .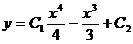

Замечание

Аналогичным способом можно решать уравнение .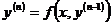

Полагая 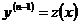, получим для определения 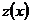уравнение первого порядка 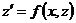. Решая это уравнение, находим его общее решение 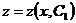. Затем из соотношения 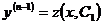находи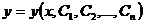м путем 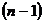- кратного интегрирования.

III тип. Уравнение вида 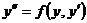, т.е. уравнение не содержит явным образом .

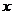Для его решения вводим новую функцию 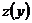, полагая 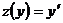, т.е. будем считать, что 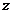есть функция от 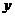(а не от 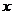, как прежде). Тогда по теореме о производной сложной функции имеем:

.

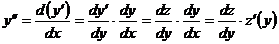Подставляя в уравнение выражения для 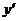и 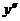, получаем уравнение первого порядка относительно 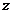как функции от :

.

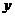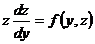Решая его, найдем 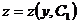. Так как 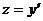, то 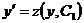. Разделяя переменные, получим .

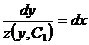Интегрируя это уравнение, находим общее решение данного уравнения:

,

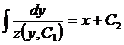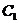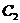где и - произвольные постоянные.

Пример 4 Найти частное решение уравнения 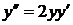, удовлетворяющее начальным условиям: .

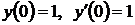Решение: Полагая 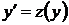и учитывая, что 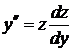, получаем .

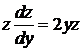Отсюда 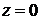или ,или .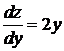

В первом случае 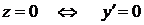, т.е. 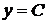. Но это решение не удовлетворяет начальным условиям. Во втором случае, из 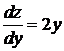следует 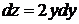, т.е. 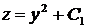. Учитывая, что 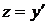и начальное условие 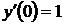, получаем 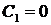. Поэтому имеем 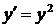или 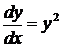. Разделяя переменные, будем иметь 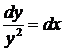или 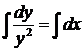. Отсюда .

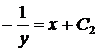Из начального условия 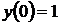находим, что 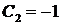. Таким образом, искомое решение задачи Коши есть функция

.

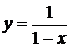Задания для самостоятельного решения

Найти общие решения уравнений:

1) ,

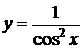2) ,

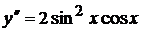3) ,

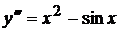4) ,

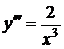5) ,

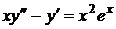6) ,

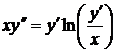7) ,

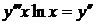8) ,

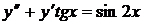9) ,

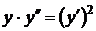10) ,

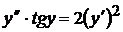11) ,

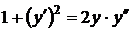12) .

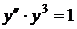Найти частные решения, удовлетворяющие заданным начальным условиям:

13) , , ;

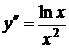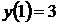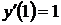14) , , ;

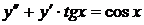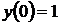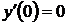15) , , .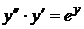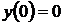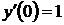