Анализ схемы принятия решений и разработка предложений по совершенствованию управления в подразделении

На заключительном этапе необходимо произвести неформальную оценку управленческих процессов в под­разделении. Обосновать, кто и как готовит и утверждает конкретные управленческие решения, какие документы необходимы для подготовки каждого решения, каковы уровни их подготовки и уровни окончательного утвер­ждения решений.

Можно говорить о степени загруженности сотрудни­ков и при необходимости внести предложения по пере­распределению обязанностей. Полученный фактологиче­ский материал позволяет судить о необходимости введе­ния дополнительной штатной единицы, либо о ее сокра­щении. В итоге можно дать оценку эффективности функ­ционирования подразделения, определить пути наилуч­шего достижения поставленных целей и грамотно исполь­зовать методы мотивации сотрудников.

Все предложения должны быть отражены в разрабо­танном новом варианте схемы принятия решений и долж­ностных инструкций.

В заключении хочется отметить следующее. Освоение и практическое использование данного подхода поможет вам стать настоящими менеджерами - исследователями своей организации, облегчит поиск путей и методов ее совершенствования и в итоге поможет добиться устой­чивого конкурентного преимущества.

Авторы искренне желают вам успехов в столь важном и не менее интересном творчестве.

Тесты

Выберите правильные ответы:

1. Система управления - это:

1) совокупность действий, определяющих направле­ние управленческой деятельности;

2) совокупность взаимосвязанных элементов в про­странстве;

3) субъект управления организацией, имеющей ие­рархическое строение.

2. Системный анализ - это:

1) конструктивное направление исследования про­цессов управления;

2) совокупность методов и моделей, направленных на решение задач исследования организации;

3) методы изучения задач системы управления.

3. Комплексное исследование систем управления предполагает:

1) изучение условий и факторов деятельности системы;

2) изучение механизма функционирования системы;

3) изучение схемы управления системы.

4. Исследование систем управления как систем принятия решений осуществляется:

1) параметрическим исследованием;

2) экспертным методом;

3) организационным моделированием;

4) факторным анализом.

5. Глобальная цель функционирования — это:

1) цель всей организации;

2) цель отдельного структурного подразделения;

3) цель отдельного руководителя.

6. Критический путь сетевой модели — это:

1) самый длинный путь;

2) самый короткий путь.

7. Эффективность управления - это:

1) одни из итоговых характеристик управления;

2) соотношение результата управленческой деятель­ности и затраченных ресурсов;

3) показатель деятельности отдельных исполнителей и руководителей.

8. Исследование организационных структур предполагает:

1) исследование функционального разделения труда;

2) исследование технологии принятия управленческих решений;

3) исследование состава и численности структурных подразделений на каждом уровне управления.

9. Проектирование систем управления осуществляется с целью:

1) анализа систем управления;

2) оптимизации систем управления;

3) изменения штатного расписания.

10. Проектирование управленческих решений необходимо в связи с:

1) совершенствованием организационной технологии;

2) исследованием целей организации;

3) мотивацией сотрудников.

Список литературы

1. Беляев А.А., Короткое Э.М. Системология. — М.: ИНФРА-М, 2000.

2. Валуев С.А., Волкова В.Н., Игнатьева А.В. и др. Системный анализ в экономике и организации производства. - Л.: По­литехника, 1991.

3. Валуев С.А, Игнатьева А.В. Организационный менеджмент. — М.: Машиностроение, 1993.

4. Герчикова И.Н. Менеджмент. - М.: ЮНИТИД995.

5. Голубков Е.П. и др. Маркетинг: выбор лучшего решения. — М.: Экономика, 1993.

6. Короткое Э.М. Исследование систем управления. — М.: «ДеКА», 2000.

7. Короткое Э.М. Концепция менеджмента. — М.: «ДеКА, 1996.

8. Максимцов М.М., Игнатьева А.В., Комаров М.А. и др. Ме­неджмент, М.: ЮНИТИ, 1998.

9. Ременников В.Б. Разработка управленческого решения. Учеб. пособие. — М.: ЮНИТИ-ДАНА, 2000.

10. Романов А.И. и др. Маркетинг. - М.: Банки и маркетинг, ЮНИТИ, 1995.

11. Словарь-справочник менеджера./Под ред. М.Г. Лапусты. — М.: ИНФРА, 1996.

12. Скоун Т. Управленческий учет./Пер. с англ, под ред. Н.Д. Эриашвили. — М.: ЮНИТИ, 1997.

13. Справочник директора предприятия. /Под ред. М.Г. Ла­пусты. — М.: ИНФРА, 1998.

14. Смолкин A.M. Менеджмент: основы организации. — М.: ИНФРА-М, 1999.

15. Управление организацией. /Под ред. А.Г. Поршнева, З.П. Румянцевой, Н.А. Саломатина. —М.: ИНФРА-М, 1999.

Образцы выполняемых студентами работ

Федеральное агентство по образованию

Южно-Уральский государственный университет

Факультет экономики и предпринимательства

КАФЕДРА Предпринимательство и менеджмент

КУРСОВАЯ РАБОТА

По курсу Исследование систем _ _

_ _ управления __ ______

____________________________________

Тема _Решение оптимизационных задач

Выполнил студент _

Группа ЭиП- _ _

Проверил _ Гельруд _

_ Ян Давидович _

Челябинск

2008 г.

ОГЛАВЛЕНИЕ

1. Задача линейного программирования 4

2. Транспортная задача. 7

3. Задача сетевого моделирования. 12

4. Задача управления запасами.............................................................................................. 4

4.1 Детерминированная статическая модель без дефицита....................................... 4

4.2 Детерминированная статическая модель с дефицитом........................................ 5

4.3 Вероятностная модель.................................................................................................. 6

5. Задача массового обслуживания..................................................................................... 7

5.1 Одноканальная система обслуживания с неограниченной очередью........... 8

5.2 Одноканальная система обслуживания с ограниченной очередью............... 9

5.3 Многоканальная система обслуживания с неограниченной очередью....... 10

5.4 Многоканальная система обслуживания с ограниченной очередью............. 11

6. Теория игр........................................................................................................................... 13

Список использованной литературы................................................................................ 16

Задача №1

Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.

1. По данным, приведенным в таблице 1.1 составить систему математических

зависимостей (неравенств) и целевую функцию.

2. Изобразить геометрическую интерпретацию задачи и найти оптимальное решение.

3. Провести аналитическую проверку и определить значение целевой функции.

4. Определить какие ресурсы и в каком количестве имеются в избытке.

5. Вычислить объективно обусловленные оценки.

6. Исследовать устойчивость решения.

Таблица 1.1 – Матрица удельных нормативов.

	Нормы на одно изделие	Прибыль на одно изделие
Ресурс 1	Ресурс 2	Ресурс 3
Изделие 1			6.4
Изделие 2	1.6	4.2	3.2
Наличие ресурсов

Решение:

1. Ограничения: 1) Х₁ ; Х₂ ≥ 0

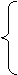2) 8 Х₁ + 1.6 Х₂ ≤ 220

2 Х₁ + 4.2 Х₂ ≤ 170 (1.1)

6.4 Х₁ + 3.2 Х₂ ≤ 240

Целевая функция: F = 35 Х₁ + 55 Х₂ → max. (1.2)

2. Геометрическая интерпретация задачи изображена на рисунке 1.1. Область решения системы уравнений (1.1) заштрихована. В точке А (22; 29,5) значение целевой функции максимально.

3. Находим оптимальное решение аналитическим методом. Для этого решим систему уравнений:

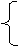8 Х₁ + 1.6 Х₂ = 220

2 Х₁ + 4.2 Х₂ = 170 (1.3)

Решаем систему методом Крамера, для этого находим определители

системы:

∆ = 8 * 4,2 –1,6 * 2 = 30,4

∆₁ = 220 * 4,2 –1,6 * 170 = 652

∆₂ = 8 * 170 – 220 * 2 = 920

Находим значения Х₁ и Х₂ :

Х₁ = ∆₁ / ∆ = 652 / 30,4 = 21,45

Х₂ = ∆₂ / ∆ = 920 / 30,4 = 30,26

Погрешность решения геометрическим способом объясняется неточностью

построения прямых и составляет: ∆Х₁ = | 21,45 – 22 | = 0,55;

∆Х₂ = | 30,26 – 29,5 | = 0,76;

Находим значение целевой функции в точке А:

F^* = 35 * 21,45 + 55 * 30,26 = 2415,05

4. Ресурсы 1 и 2 являются существенными и полностью использовались. А ресурс 3 - в избытке, который равен: И = 240 – (6,4 * 21,45 + 3,2 * 30,26) = 5,9.

5. Вычисляем ООО ресурсов (Y₁ , Y₂ , Y₃).

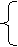1) для 1-го ресурса: 8 Х₁ + 1.6 Х₂ = 220 + 1

2 Х₁ + 4.2 Х₂ = 170 (1.4)

Решаем систему методом Крамера, для этого находим определители

системы:

∆ = 8 * 4,2 –1,6 * 2 = 30,4

∆₁ = 221 * 4,2 –1,6 * 170 = 656,2

∆₂ = 8 * 170 – 221 * 2 = 918

Находим значения Х₁ и Х₂ :

Х₁ = ∆₁ / ∆ = 656,2 / 30,4 = 21,59

Х₂ = ∆₂ / ∆ = 918 / 30,4 = 30,2

Находим значение целевой функции:

F^* ₁ = 35 * 21,59 + 55 * 30,2 = 2416,65

Y₁ = F^* ₁ - F^* = 2416,65 – 2415,05 = 1,6

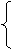2) для 2-го ресурса: 8 Х₁ + 1.6 Х₂ = 220

2 Х₁ + 4.2 Х₂ = 170 + 1 (1.5)

Решаем систему методом Крамера, для этого находим определители

системы:

∆ = 8 * 4,2 –1,6 * 2 = 30,4

∆₁ = 220 * 4,2 –1,6 * 171 = 650,4

∆₂ = 8 * 171 – 220 * 2 = 928

Находим значения Х₁ и Х₂ :

Х₁ = ∆₁ / ∆ = 650,4 / 30,4 = 21,39

Х₂ = ∆₂ / ∆ = 928 / 30,4 = 30,53

Находим значение целевой функции:

F^* ₂ = 35 * 21,39 + 55 * 30,53 = 2427,8

Y₂ = F^* ₂ - F^* = 2427,8 – 2415,05 = 12,75.

3) Y₃ = 0, т.к. рост этого ресурса не принесет дополнительной прибыли,

поскольку его избыток.

Таким образом, наибольшее значение ООО имеет второй ресурс и

увеличение его на единицу приведет к увеличению прибыли на 12,75

единиц.

6. Исследуем устойчивость решения:

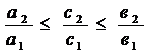Решение считается устойчиво, если выполняется условие (1.6):

	(1.6)

Где а₂, а₁ - коэффициенты в первом уравнении системы уравнений (1.3)

с₂, с₁ - коэффициенты в формуле целевой функции (1.2)

в₂, в₁ - коэффициенты во втором уравнении системы уравнений (1.3)

Подставим в условие (1.6) значение коэффициентов:

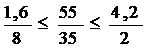
0,2 ≤ 1,57 ≤ 2,1

Т.е условие выполняется, а значит решение устойчиво.

С геометрической точки зрения решение считается устойчивым, когда нормаль n₁ к прямой , выражающей целевую функцию, находится между нормалями n₂ n₃ к прямым, ограничивающими ресурсы 1 и 2. На рисунке 1.1 видно, что так оно и есть.

Задача №2

Найти оптимальное решение транспортной задачи, исходные данные которой представлены в таблице 2.1.

1. Свести задачу к закрытому типу (при необходимости).

2. Найти базисный план (методом северо-западного угла или любым другим).

3. Проверить этот базисный план на оптимальность методом потенциалов.

4. Выполнить итерации по улучшению плана до получения оптимального решения (после каждой итерации вычислять значение целевой функции).

Таблица 2.1 – Исходные данные для транспортной задачи.

	В1 = 35	В2 = 43	В3 = 110	В4 = 72	В5 =
А1 = 70
А2 = 80
А3 = 40
А4 = 60
А5 =

1. Определяем тип задачи. Для этого просчитаем сумму поставляемых и потребляемых единиц товара: ∑А_i = 70 + 80 + 40 + 60 = 250

∑В_j = 35 + 43 + 110 + 72 = 260

Т.к. ∑А_i ≠ ∑В_j , то наша задача является задачей открытого типа.

Чтобы превратить задачу в задачу закрытого типа добавим дополнительную строку с фиктивным поставщиком с объемом производства в 10 единиц с нулевыми удельными затратами на перевозку. Тогда таблица 2.1 примет следующий вид (см. таблицу 2.2)

Таблица 2.2 – Задача закрытого типа

2. Находим базисный план методом северо-западного угла (см. таблицу 2.3)

Таблица 2.3 – Базисный план перевозок

	5 35	2 35
		3 8	4 72
			3 38	4 2
				6 60
				0 10

Находим значение целевой функции F^* = ∑ затрат → min

F^* = 35 * 5 + 35 * 2 + 8 * 3 + 72 * 4 +38 * 3 + 2 * 4 + 60 * 6 + 10 * 0 = 1039

Находим оценку пустых клеток и если эта величина будет отрицательной, то значение целевой функции для нового плана перевозок будет меньше базового.

Находим ∆₂₁ = 1 – 5 + 2 – 3 = - 5. Тогда перемещаем в клетку 2.1 минимальное значение из отрицательных вершин контура, т.е 8 единиц.

Таблица для первой итерации примет вид (см. таблицу 2.4):

Таблица 2.4 – 1-я итерация

	5 27	2 43
	1 8		4 72
			3 38	4 2
				6 60
				0 10

Находим значение целевой функции для данного плана:

F^* = 27 * 5 + 43 * 2 + 8 * 1 + 72 * 4 +38 * 3 + 2 * 4 + 60 * 6 + 10 * 0 = 999

Находи оценку для клетки 1.3: ∆₁₃ = 2 – 5 + 1 – 4 = - 6.

Делаем 2.-ю итерацию для плана перевозок аналогично первой, тогда план примет следующий вид (см. таблицу 2.5):

Таблица 2.5 – 2-я итерация

		2 43	2 27
	1 35		4 45
			3 38	4 2
				6 60
				0 10

Находим значение целевой функции для данного плана:

F^* = 43 * 2 + 27 * 2 + 35 * 1 + 45 * 4 + 38 * 3 + 2 * 4 + 60 * 6 + 10 * 0 = 837

Находи оценку для клетки 4.3: ∆₄₃ = 1 – 3 + 4 – 6 = - 4.

Делаем 3-ю итерацию для плана перевозок аналогично предыдущим, тогда план примет следующий вид (см. таблицу 2.6):

Таблица 2.6 – 3-я итерация

		2 43	2 27
	1 35		4 45
				4 40
			1 38	6 22
				0 10

Находим значение целевой функции для данного плана:

F^* = 43 * 2 + 27 * 2 + 35 * 1 + 45 * 4 + 40 * 4 + 38 * 1 + 22 * 6 + 10 * 0 = 685

Находи оценку для клетки 1.4: ∆₁₄ = 1 – 2 + 1 – 6 = - 6.

Делаем 4-ю итерацию для плана перевозок аналогично предыдущим, тогда план примет следующий вид (см. таблицу 2.7):

Таблица 2.7 – 4-я итерация

		2 43	2 5	1 22
	1 35		4 45
				4 40
			1 60
				0 10

Находим значение целевой функции для данного плана:

F^* = 43 * 2 + 5 * 2 + 22 * 1 + 35 * 1 + 45 * 4 + 40 * 4 + 60 * 1 + 10 * 0 = 553

Находи оценку для клетки 2.2: ∆₂₂ = 3 – 2 + 2 – 4 = - 1.

Делаем 5-ю итерацию для плана перевозок аналогично предыдущим, тогда план примет следующий вид (см. таблицу 2.8):

Таблица 2.8 – 5-я итерация

			2 48	1 22
	1 35	3 43	4 2
				4 40
			1 60
				0 10

Находим значение целевой функции для данного плана:

F^* = 48 * 2 + 22 * 1 + 35 * 1 + 43 * 3 + 2 * 4 + 40 * 4 + 60 * 1 + 10 * 0 = 510

Находи оценку для клетки 3.3: ∆₃₃ = 3 – 2 + 1 – 4 = - 2.

Делаем 6-ю итерацию для плана перевозок аналогично предыдущим, тогда план примет следующий вид (см. таблицу 2.9):

Таблица 2.9 – 6-я итерация

			2 8	1 62
	1 35	3 43	4 2
			3 40
			1 60
				0 10

Находим значение целевой функции для данного плана:

F^* = 8 * 2 + 62 * 1 + 35 * 1 + 43 * 3 + 2 * 4 + 40 * 3 + 60 * 1 + 10 * 0 = 430

Находи оценку для клеток 3.1: ∆₃₁ = 5 – 1 + 4 – 3 = 5.

3.2: ∆₃₂ = 3 – 3 + 4 – 3 = 1.

4.1: ∆₄₁ = 3 – 1 + 4 – 1 = 5.

4.2: ∆₄₂ = 2 – 3 + 4 – 1 = 2.

5.3: ∆₅₃ = 0 – 2 + 1 – 0 = - 1.

Делаем 7-ю итерацию для плана перевозок аналогично предыдущим, тогда план примет следующий вид (см. таблицу 2.10):

Таблица 2.10 – 7-я итерация

				1 70
	1 35	3 43	4 2
			3 40
			1 60
			0 8	0 2

Находим значение целевой функции для данного плана:

F^* = 70 * 1 + 35 * 1 + 43 * 3 + 2 * 4 + 40 * 3 + 60 * 1 + 8 * 0 + 2 * 0 = 422

Таким образом, оптимальный план перевозок найден и величина удельных издержек составит 422 единицы.

Задача №3

1. Построить фрагмент сетевого графика, согласно заданному порядку предшествования работ.

А, В, С « D;

A, C « E;

A, B « G;

B, E « H;

B H

D

G E

A

С

Рисунок 3.5 - Фрагмент сетевого графика

2. Провести расчет временных параметров сетевой модели и приведение критического времени к заданному сроку.

22 10 12

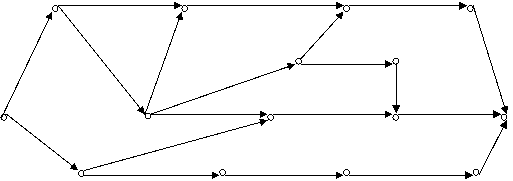
11 12 18 12 5

8 8 5

17 10

10 6 8

Рисунок 3.1 – Схема проведения работ

2.1 Рассчитать временные параметры:

Т⁰_i - ранние сроки свершения событий;

Т¹_i - поздние сроки свершения событий;

Т_кр - критическое время;

R_iⁿ_j - полные резервы работ;

R_i^с_j - свободные резервы работ;

Определить критический путь (КП).

2.2 R_iⁿ_j и R_i^с_j занести в таблицу.

2.3 Привести Т_кр к Т_дир. (Т_дир =72 дня).

2.4 Выполнить расчет сетевого графика и убедиться, что Т_кр = Т_дир ; выполнить расчет временных параметров.

Решение: ранние и поздние сроки свершения событий занесем в левый и правый сектор вершины

2 10 13 14

12 12 42 42 52 52 64 64

0 0 0 0

8 11

40 41 45 72

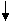
1 27

1

0 0 5 7 12 15

0 30 30 38 69 50 77 82 82

0 31 27 0

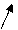
3 4 6 9

17 46 27 56 33 62 41 70

29 29 29 29

Рисунок 3.2 - фрагмент сетевого графика

Заносим в таблицу необходимые параметры сетевого графика (см. табл. 3.1).

Таблица 3.1 - Параметры сетевого графика

i,j	ti,j	Т0i	Riпj	Riсj
1,2
1,3
2,5
2,10
3,4
3,7
4,6
5,7
5,8
5,10
6,9
7,12
8,11
8,13
9,15
10,13
11,12
12,15
13,14
14,15

Приводим Т_кр к Т_дир. (Т_дир =72 дня). Для этого сократим время исполнения работ 13,14 и 14,15 на 4 и 6 дней соответственно за счет привлечения дополнительных ресурсов.

Тогда сетевой график будет выглядеть, как изображено на рисунке 3.3. А параметры откорректированного графика приведены в таблице 3.2.

На основе параметров сетевого графика, приведенных в таблице 3.2, строим календарный график работ (см. рисунок 3.4).

Таблица 3.2 - Параметры откорректированного сетевого графика

i,j	ti,j	Т0i	Riпj	Riсj
1,2
1,3
2,5
2,10
3,4
3,7
4,6
5,7
5,8
5,10
6,9
7,12
8,11
8,13
9,15
10,13
11,12
12,15
13,14
14,15

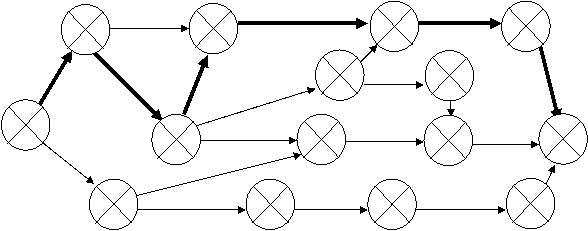
2 10 13 14

12 12 42 42 52 52 60 60

0 0 0 0

8 11

40 41 45 62

1 17

0 0 5 7 12 15

0 30 30 38 59 50 67 72 72

0 21 17 0

3 4 6 9

17 36 27 46 33 52 41 60

19 19 19 19

Рисунок 3.3 - Корректированный фрагмент сетевого графика

Задача управления запасами