Графические методы расчета нелинейных цепей постоянного тока

Чаще всего применяют кусочно-линейную аппроксимацию, когда всю ВАХ заменяют на совокупность отрезков прямых. Каждый отрезок ВАХ описывают линейным уравнением (U=a+bi). Этому уравнению сопоставляют некоторую схему замещения. Для каждого участка аппроксимации нелинейный элемент заменяют его схемой замещения. Задача становиться линейной. Можно применять все методы расчёта линейных цепей.

Заранее неизвестно, какой нужно выбрать участок ВАХ. Поэтому берут какой-то один. Рассчитывают режим цепи. Проверяют, попала ли рабочая точка в тот диапазон U и I, для которого использован данный участок аппроксимации. Если не попала, то берут следующий участок ВАХ и так повторяют до тех пор, пока не получится совпадение. Во всех аналитических методах очень важно оценить возможное положение рабочей точки, т. к. это позволяет аппроксимировать не всюВАХ, а только её часть.

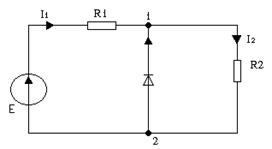
Из схемы видно, что к диоду приложено обратное напряжение, поэтому аппроксимировать нужно обратную ветвь. Обратную ветвь заменяют двумя прямыми линиями.

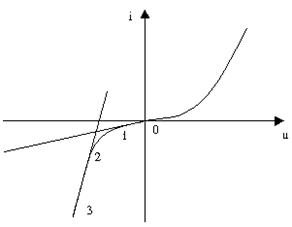
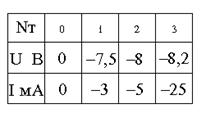
U = a₁ + b₁I, если -3 ≤ I ≤ 0

U = a₂ + b₂I, если -25 < I < -5

При U = 0: a₁ = 0

При U = -7,5: b₁ = 2500 Ом

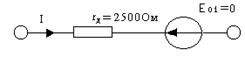
При U = -8: a₂ + (-5∙10³)b₂ = -8 (1)

При U = -8,2: a₂ + (-25∙10³)b₂ = -8,2 (2)

Вычтем из (1) уравнения (2) и получим: b₂ = 10 Ом, a₂ = -7,95 В.

Пусть E = 24 В, R₁ = 1500 Ом, R₂ = 3000 Ом. Начнем со второго участка, тогда полученная схема замещения.

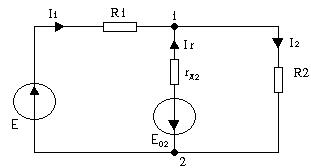
φ₂ = 0

φ₁(1/R₁+1/r_д2 + 1/R₂) = E/R₁ - E₀₂/r_д2

φ₁ = (E r_д2 R₂ - E₀₂R₁R₂)/(r_д2 R₂ + R₁R₂ + R₁r_д2)=8,03 В

Рабочая точка оказалась на втором участке ВАХ, который мы и использовали. Режим для нелинейного элемента найден правильно. При необходимости рассчитывают остальные токи и напряжения методами уже линейной цепи

3) Графические - эти методы основаны на графическом решении уравнений Кирхгофа, т. к. других уравнений писать нельзя (несколько проще решают задачи с одним нелинейным элементом). При графическом решении складывают или вычитают либо напряжения на каких то участках, либо токи в некоторых ветвях. При этом любые две величины можно складывать только тогда, когда у них одинаковый аргумент.

Рассматривают некоторыеграфические методы: метод эквивалентного генератора; расчет последовательного, параллельного и смешанного соединения нелинейных элементов;метод двух узлов; расчёт цепи с управляемым нелинейным элементом.

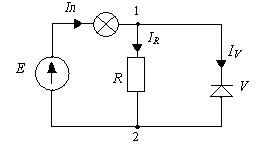
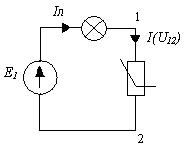
Пример 1: Цепь содержит один нелинейный элемент.

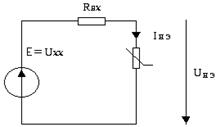
В этом случае удобно применять метод эквивалентного генератора.

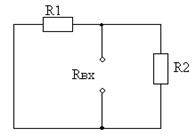
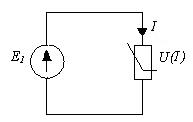
1) Нелинейный элемент считают нагрузкой, а всё остальное - активным двухполюсником. Находят параметры двухполюсника: Uxx, Rвх, Iкз.

2) Получают такую задачу, для которой справедливо: (*)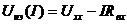

Левая часть - это ВАХ нелинейного элемента, а правая – линейная функция тока I и её строят по двум любым точкам.

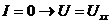
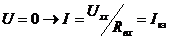
Строят левую и правую часть уравнения (*)

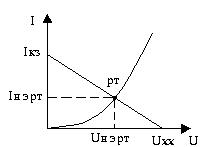
3) По полученным величинам в рабочей точке нелинейный элемент заменяют по теореме компенсации либо источником ЭДС, либо источником тока.

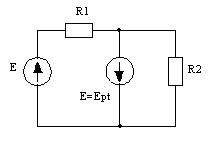
При этом получают полностью линейную задачу, а значит все остальные токи и напряжения можно рассчитать любым эффективным методом. Решим ту же задачу, что и выше.

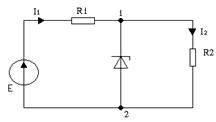
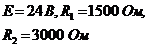
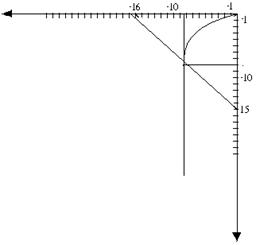
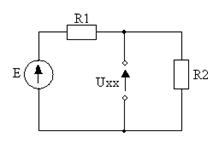
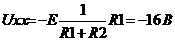
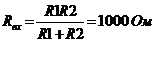
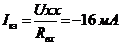
Видно, что удобно заменить источником ЭДС.

Пример 2: Расчет последовательного, параллельного и смешанного соединения нелинейных элементов.

а) Последовательное соединение

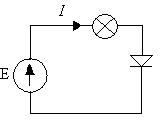
Е = Uл(I)+Uv(I).

Чтобы построить ВАХ правой части уравнения, несколько раз задают произвольное значение тока I и суммируют получившиеся значения напряжений на элементах. График левой части есть вертикальная линия.

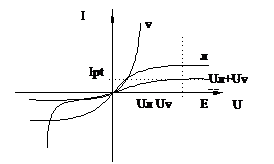
По пересечению графиков правой и левой частей уравнения находят величину тока в рабочей точке I_р.т. Зная I_р.т, по ВАХ каждого элемента находят Uл и Uv.

б) Параллельное соединение

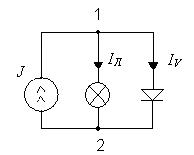
J = Iл(U₁₂)+Iv(U₁₂)

Из уравнения видно, что надо задавать значение U и суммировать полученные значения токов. Получают график правой части. График левой части – горизонтальная линия.

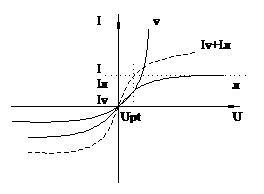
Получив Uрт, по графику ВАХ каждого нелинейного элемента находят ток.

в) Смешанное соединение

Начинают преобразовывать схему с самого дальнего от источника участка, заменяя последовательное и параллельное соединение нелинейных элементов некоторыми эквивалентными нелинейными элементами. ВАХ этих элементов получают в соответствии с уравнениями Кирхгофа. Так делают до тех пор, пока не получат схему с одним источником и одним нелинейным элементом. Рассчитывают режим этой схемы. Используя полученные величины, возвращаются шаг за шагом назад и находят остальные токи и напряжения.

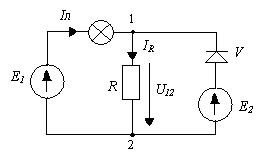
Преобразуем правую часть:

U₁₂(Iv)+Uv(Iv)=E₂

U₁₂(Iv) =E₂-Uv(Iv)

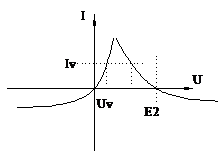
U₁₂(Iл)+Uл(Iл)=E₁

U₁₂(Iv)+Uv(Iv)=E₂

U₁₂(IR)-UR=0

Iл(U₁₂)+Iv(U₁₂)=I_R

Заменим две правые ветви одним эквивалентным элементом:

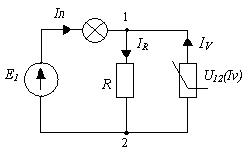
I_∑(U₁₂) = I_R(U₁₂) - Iv(U₁₂) (1)

Для построения ВАХ правой части уравнения (1)задают значения U и по ВАХ R и диода при данном U суммируют токи. Строят график правой части уравнения (1) - U₁₂(I).

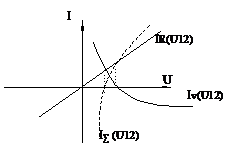
I_Л=I_∑ и уравнение цепи имеет вид:

Е = Uл(I_∑)+ U₁₂(I_∑) (2).

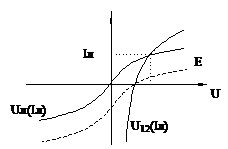
По пересечению полученного графика правой части уравнения (2) и ВАХ ЭДС Е₁, находят Iл. Зная Iл, по ВАХ лампы находят Uл; по ВАХ U₁₂ (I) -U₁₂. По полученному U₁₂, определяют I_R по ВАХ I_R (U₁₂) и по ВАХ Iv(U₁₂) - Iv. По ВАХ диода и известному току Iv получают Uv.

г) Расчёт цепи с управляемым нелинейным элементом

В этих задачах мы имеем не одну какую-то ВАХ, а два семейства ВАХ и порядок действия может быть таким.

1) Записывают уравнения по законам Кирхгофа (но от управляемого элемента берут только такие токи и напряжения, которые указаны на осях его ВАХ).

2) Методом подстановки всю систему сводят до двух уравнений, которые должны содержать только параметры элементов схемы и токи и напряжения нелинейного элемента.

3) Графически решают полученные два уравнения.

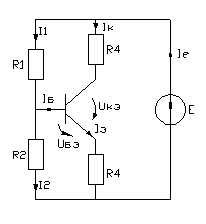I_E = Iк+I₁ (1)

I₁ = I₂+I_б (2)

Iк+I_б = Iэ (3)

I₁R1+I₂R2 = E (4)

IкR3+Uкэ+IэR4 = E (5)

Uбэ+IэR4- I₂R2 = 0 (6)

Т.к. Iк >> I_б то из уравнения (3)

Iк = Iэ.

Из уравнения (2) Выразим I₁ и подставим в (4). Получим:

I₂R1+ I_бR1+ I₂R2 = E (7)

IкR3+Uкэ + IкR4 = E (8)

Uбэ + IкR4 - I₂R2 = 0 (9)

Из (7) выражаем I₂ и подставляем в (9):

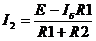
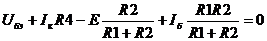(10)

Уравнения (8) и (10) соответствуют требованиям и мы будем их решать.

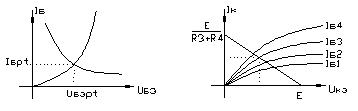
Выразим из (8) Uкэ: Uкэ = Е-Iк (R3-R4).

Левая часть это ВАХ, а правая – уравнение прямой линии (нагрузочной прямой). Решение лежит где-то на этой прямой, но мы не знаем, какой I_б соответствует РТ и поэтому не можем указать конкретную ВАХ. Воспользуемся уравнением (10):

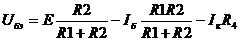
Левая часть - это ВАХ, а правую строят так: задают значение I_б, на выходных ВАХ находят ток коллектора (пересечение прямой с выбранной ВАХ) и вычисляют правую часть. Эту процедуру повторяют несколько раз и строят график U_бэ(I_б). На входной ВАХ находят пересечение с полученным график U_бэ(I_б). Точка пересечения указывает положение рабочей точки (U_бэрт, I_брт).). После этого на выходных ВАХ выбирают, соответствующую найденному I_брт, характеристику. По точке пересечение полученной выходной характеристикой с нагрузочной прямой находят Uкэ_РТ и Iк_РТ. По координатам рабочей точки выбирают транзистор по мощности: Р_{к доп} > U_КЭрт ∙I_Крт

Метод двух узлов