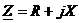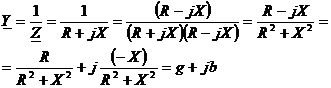Законы цепей в символической форме

1. Первый закон Кирхгофа

Алгебраическая сумма мгновенных значений токов ветвей, сходящихся в одном узле, равна нулю. .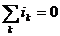

Подставим вместо каждого мгновенного значения тока его представление в виде комплекса амплитудного значения, тогда .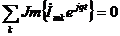

Так как в любой момент времени нулю равна сумма проекций вращающихся векторов, следовательно, нулю должна равняться сумма самих вращающихся векторов, т.е. получим 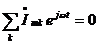. Так как 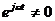, то сократим на нее и получим .

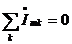Алгебраическая сумма комплексов амплитудных значений токов ветвей, сходящихся в одном узле, равна нулю.

Поделив на 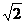, получим первый закон Кирхгофа для комплексов действующих значений.

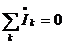
2. Второй закон Кирхгофа

После аналогичных преобразований получим:

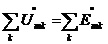или .

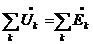Алгебраическая сумма комплексов амплитудных (действующих) значений напряжений на всех элементах контура, кроме ЭДС равна алгебраической сумме комплексов амплитудных (действующих) значений ЭДС этого же контура.

Однако для самих амплитудных и действующих значений законы Кирхгофа не выполняются.

3.6 Фазовые соотношения между напряжением и током на элементах R,L,C

Комплексы амплитуд напряжения и тока на элементах R,L,C связаны между собой.

Для R:

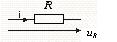
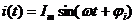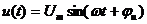, , где U_m=RI_m,, j_u=j_i

Перейдем к проекциям вращающихся векторов:

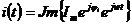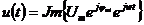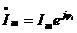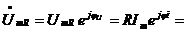
, => Так как , 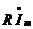. Тогда

:

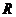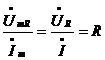
Для L:

,

.

,

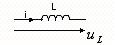
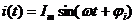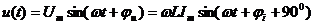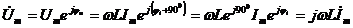j_u=j_i + 90⁰.

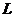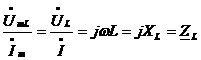: - комплексное сопротивление индуктивности.

Для C:

,

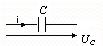
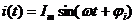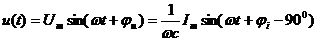
j_u=j_i - 90⁰.

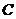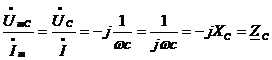: - комплексное сопротивление емкости.

Таким образом, для любого элемента в цепи синусоидального тока 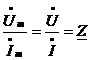- некоторое комплексное число по размерности оно соответствует сопротивлению, и поэтому его называют комплексом полного сопротивления и обозначают 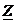. Тогда:

,

,

.

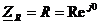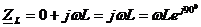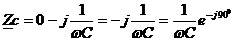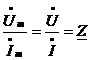представляет закон Ома в символической форме.

Комплекс полного сопротивления участка пассивной цепи синусоидального тока рассчитывают так же, как в цепи постоянного тока, если вместо элементов участка использовать комплексные сопротивления этих элементов.

,

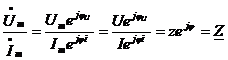где:

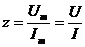- коэффициент пропорциональности между амплитудными или действующими значениями напряжения и тока на данном элементе;

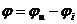показывает на сколько фаза напряжения больше фазы тока на данном элементе.

Иногда строят треугольник сопротивлений. Фактически это и есть изображение комплекса полного сопротивления на комплексной плоскости.

Величина 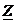, как любое комплексное число, может быть представлена в показательной, тригонометрической или алгебраической форме:

,

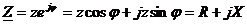где 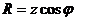- вещественная часть комплекса полного сопротивления, ее называют активной составляющей комплекса полного сопротивления;

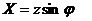- мнимая часть комплекса полного сопротивления, ее называют реактивной составляющей комплекса полного сопротивления;

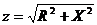- модуль комплекса полного сопротивления;

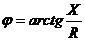- фаза комплекса полного сопротивления, изменяется в пределах .

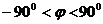Величину обратную комплексу полного сопротивления называют комплексом полной проводимости (КПП):

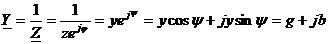, где

.

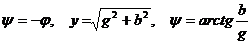Для получения в «буквах» активной и реактивной составляющих комплекса полной проводимости по заданным в «буквах» активной и реактивной составляющим комплекса полного сопротивления: