Расчет режима простейших цепей (метод сворачивания или свертки)

Простейшие цепи – это цепи с одним источником энергии и не очень сложной структурой, включающей либо последовательно, либо параллельно соединенные пассивные элементы.

Примерный порядок расчета.

1. Выбирают положительное направление токов ветвей и нумеруют все узлы схемы.

2. Начиная с самого удаленного от источника участка цепи, находят эквивалентные сопротивления участков с последовательным или параллельным соединением элементов. Процесс продолжают до тех пор, пока не получится одноконтурная схема.

3. В полученной схеме находят либо неизвестный ток I_вх, либо неизвестное напряжение U_вх в зависимости от источника схемы.

4. Двигаясь в обратной последовательности, рассчитывают неизвестные токи и напряжения, используя закон Ома и первый закон Кирхгофа.

5. Проверку правильности расчета режима цепи проводят по балансу мощностей или законам Кирхгофа.

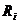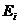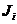Пример: Дано: , или . Найти: .

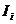Рис. 2.2.1

.

Рис. 2.2.2

.

Рис. 2.2.3

.

Рис. 2.2.4

.

Рис. 2.2.5

Неизвестное напряжение находят по закону Ома: .

Возвращаются к схеме рис. 2.2.4 и определяют неизвестные напряжения по закону Ома: и .

Переходят к схеме рис. 2.2.3 и вычисляют неизвестные токи: , .

По схеме рис. 2.2.2 определяют ,

По схеме рис. 2.2.1 находим: , .

Проверка по балансу мощностей: , .

Закон Ома для участка цепи, содержащего источники ЭДС

Это специальное правило, позволяющее вычислять величину тока в ветви, если известно напряжение на ее зажимах.

По второму закону Кирхгофа для фиктивного контура:

=>

,

т.е.

Метод узловых потенциалов

Этот метод позволяет сократить число совместно решаемых уравнений по сравнению с методом уравнений Кирхгофа.

Идея метода состоит в следующем: если выразить ток каждой ветви по закону Ома для ветви, содержащей ЭДС и подставить полученное выражение в (n_У - 1) число уравнений первого закона Кирхгофа, получится система уравнений в относительно узловых потенциалов. Правда число потенциалов будет на единицу больше числа уравнений. Эту проблему решают так: т.к. ток в ветви зависит от разности потенциалов ее концов, не изменяя режима цепи, можно все потенциалы узлов схемы изменить на одну и ту же величину, причем на столько, чтобы один из потенциалов стал равен нулю (заземлить какой-то узел). После этого получаются уравнения стандартного вида.

Для некоторого узла k получится уравнение

,

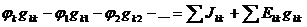где 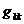- собственная узловая проводимость k-ого узла, она равна сумме проводимостей всех ветвей, подключенных к этому узлу;

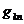- межузловая проводимость k-ого и n-ого узлов, она равна сумме проводимостей ветвей непосредственно соединяющих n-ый узел с узлом k для которого пишется уравнение;

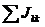- алгебраическая сумма величин источников тока, стоящих в ветвях, присоединенных к k-ому узлу;

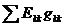- алгебраическая сумма произведений ЭДС, стоящих в ветвях присоединенных к k-ому узлу на проводимости этих ветвей.

У любого источника берется знак «+», если он направлен к узлу, для которого пишется уравнение.

Проводимость ветви есть величина обратная сопротивлению этой ветви.

Пример:

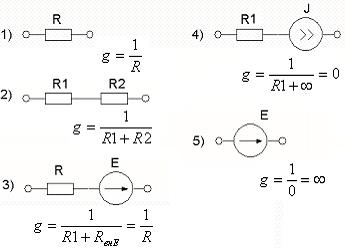
Ветвь 5) называется ветвью типа Е и проводимость вычисляется по особому правилу. Рекомендуемый порядок действий:

1. Выбирают узел, потенциал которого принимают равным нулю. Возможны 3 случая.

а. В схеме нет ветвей типа Е, тогда заземляют любой узел схемы. Записывают (n_У - 1) уравнений МУП, где n_У - число узлов схемы.

б. В схеме есть одна или несколько ветвей типа Е, но если их несколько, то все они между собой непосредственно соединены. Тогда обязательно заземляют один из узлов этих ветвей. Остальные узлы будут иметь известные потенциалы. Записывают ((n_У -1)- n_Е) уравнений

МУП, где n_Е – число ветвей типа Е.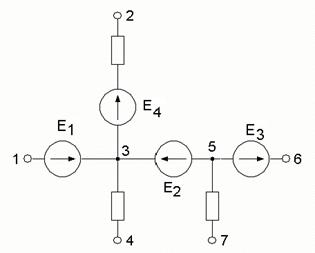

,

,

,

,

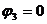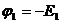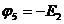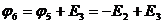в. В схеме есть несколько ветвей типа Е, но не все они между собой соединены – решать задачу МУП нельзя.

2. Для узлов, потенциалы которых остались неизвестными, записывают уравнения МУП стандартного вида и решают полученную систему.

Система уравнений должна быть полной – содержать столько уравнений, сколько неизвестных.

3. Токи ветвей записывают по закону Ома для участка цепи, содержащего ЭДС. В ветвях типа Е токи по закону Ома определить нельзя.

.

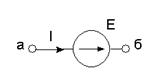
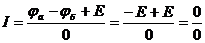Примечание: в ветвях типа Е токи находят по первому закону Кирхгофа в последнюю очередь.

Если в схеме есть управляемые источники, то к системе уравнений по МУП приписывают уравнения связи, в которых величины управляемых источников выражаются через узловые потенциалы.

Пример: Дано: 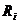, , 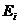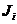. Найти: .

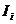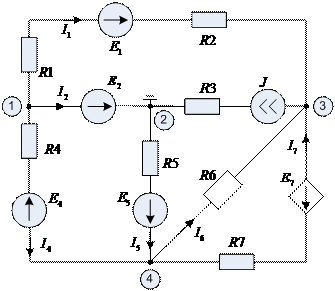
Пусть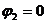

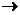
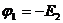
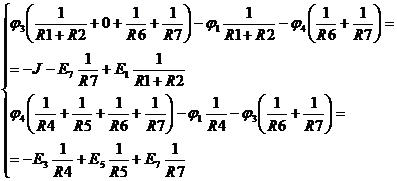
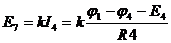
Решают эту систему и находят потенциалы 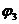и 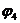. После этого находят токи ветвей:

, , , , ,

=> .

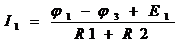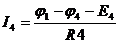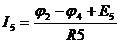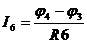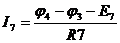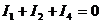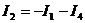Метод наложения

В любой линейной системе реакция на сумму воздействий равна сумме реакций на каждое воздействие в отдельности.

В цепях воздействие – это источники напряжения и источники тока, а реакция – это токи ветвей и напряжения между какими - то точками схемы. Поэтому любой ток или напряжение в линейной цепи с несколькими источниками равен сумме частичных значений тока или напряжения, вызванных действием каждого источника в отдельности. Свойство наложения (суперпозиции) справедливо только для токов и напряжений. Для мощностей этот принцип не выполняется, так как мощности элементов рассчитываются по нелинейным уравнениям.

Метод наложения основан на принципе наложения.

Примерный порядок расчета

1. Выбирают положительное направление токов ветвей и нумеруют все узлы схемы.

2. Исходную схему представляют в виде нескольких подсхем. В каждой подсхеме оставляют один или несколько автономных источников в общем случае одной и той же частоты, что определяется простотой расчета. Остальные автономные источники заменяют их внутренним сопротивлением. Все автономные источники должны войти в подсхемы, но только один раз.

3. Рассчитывают частичный режим в каждой подсхеме любым рациональным методом.

4. Режим в исходной схеме определяют как алгебраическую сумму частичных режимов. Если необходимо, то рассчитывают мощности.

5. Проверку правильности расчета режима цепи проводят по балансу мощностей или законам Кирхгофа.

Примечание: если в схеме есть управляемые (зависимые) источники, то их сохраняют во всех подсхемах.