Раздел i. электрические цепи

РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Конспект лекций

дисциплины

"Электротехника и электроника"

Специальность: 071900 "Информационные системы и технологии".

2007 г.

СОДЕРЖАНИЕ

Введение

РАЗДЕЛ I. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

1. Основные понятия и законы теории цепей

1.1. Основные величины

1.2. Электрическая схема и её элементы

1.3. Топологические элементы схемы

1.4. Основные законы цепей

Основные свойства и методы расчета линейных цепей постоянного тока

2.1. Метод уравнений Кирхгофа

2.2. Расчет режима простейших цепей (метод сворачивания или свертки)

2.3. Закон Ома для участка цепи, содержащего

источники ЭДС

2.4. Метод узловых потенциалов

2.5. Метод наложения

2.6. Теорема об эквивалентном генераторе

2.7. Метод эквивалентного генератора

2.8. Передача мощности от активного двухполюсника в нагрузку

2.9. Эквивалентные преобразования структуры цепи

Анализ и расчет линейных цепей синусоидального тока

3.1. Способы представления и параметры

3.2. Элементы R,L,C в цепи синусоидального тока

3.3.Алгебра комплексных чисел

3.4. Символический метод

3.5. Законы цепей в символической форме

Фазовые соотношения между напряжением и

током на элементах R,L,C

3.7. Применение символического метода

3.8. Векторные и топографические диаграммы

Мощности в цепях синусоидального тока

3.10. Передача мощности от активного двухполюсника

в нагрузку в цепи синусоидального тока

Анализ и расчет цепей с индуктивными связями

4.1. Индуктивно связанные элементы цепи

4.2.Расчёт режима цепи с индуктивными связями

4.3. Способы «замены» индуктивных связей

4.4. Трансформатор

Трехфазные цепи

5.1. Понятие о многофазных источниках питания и о многофазных цепях

5.2. Соединения звездой и многоугольником

5.3. Расчет симметричных и несимметричных режимов трехфазных цепей

Линейные цепи периодического несинусоидального тока

6.1. Способы представления и описания

6.2. Расчет режима

6.3. Мощности в цепи несинусоидального тока

Классический метод расчета переходных процессов в линейных цепях

7.1. Возникновение переходных процессов и законы

коммутации

7.2. Способы получение характеристического

уравнения

7.3. Особенности переходных процессов в цепях с

одним реактивным элементом

Переходные процессы в цепях с двумя

Разнородными реактивными элементами

Временные характеристики цепей

Особенности расчета переходных процессов в цепях с некорректными начальными условиями

Операторный метод расчета переходных процессов в линейных цепях

8.1. Применение преобразования Лапласа и его свойств к расчету переходных процессов

8.2. Переход от изображения к оригиналу. Формулы разложения

8.3. Законы цепей в операторной форме

8.4. Эквивалентные операторные схемы замещения

РАЗДЕЛ II. НЕЛИНЕЙНЫЕ ЦЕПИ

Нелинейные электрические цепи

9.1. Классификация нелинейных элементов

9.2 Параметры нелинейных элементов и некоторые

схемы их замещения

Графические методы расчета нелинейных цепей постоянного тока

Метод двух узлов

Расчет рабочей точки в цепях с управляемым нелинейным элементом

Расчет цепей синусоидального тока. Анализ

Цепей с диодом

Магнитные цепи постоянного тока

10.1. Основные величины, характеризующие

магнитное поле

10.2. Основные законымагнитных цепей

10.3. Основные характеристикимагнитных материалов

Расчет режима неразветвленной магнитной цепи

Введение

Электротехника - это наука о техническом (т.е. прикладном) использовании электрических и магнитных явлений. Большое значение электротехники заключается в том, что средствами электротехники

- эффективно получают и передают электроэнергию;

- решают вопросы

· передачи и преобразования сигналов и информации: звук человеческой речи преобразуют в электромагнитные колебания (телефон, радио);

· хранения информации (телеграф, радио, магнитная запись);

- выполняют математические операции: вычислительные машины с огромной скоростью выполняют любые математические операции, в том числе и решение сложных уравнений.

Теоретические основы электротехники заложены физикой (учением об электричестве и магнетизме) и математикой (методами описания и анализа электромагнитных явлений). Наряду с этом развитие электротехники привело к ряду новых физических понятий, новых формулировок физических законов, к развитию специальных математических методов, связанных с описанием и анализом типичных явлений, протекающих именно в электротехнических устройствах.

ЭЛЕКТРОТЕХНИКА

теория цепей теория электромагнитного поля

в основе: з. Ома, Кирхгофа ур-я Максвелла

мат. аппарат: обык. диф. ур. диф. ур. в част. производных

применение: l >> хар. разм. l » хар. разм. исслед. устр.

исслед. устр.

название: цепи с сосредоточен- цепи с распределенными па-

ными параметрами раметрами (длинные линии)

Основные величины

Основные величины в теории цепей: q, i, j, u, p. Все эти величины являются функциями времени и поэтому самое подробное описание это задание мгновенных значений либо в виде аналитического выражения, либо в виде графика. В электротехнике применяют стандартные названия и обозначения. Мгновенные значения какой-то величины –значения, зависящие от времени, обозначают строчными буквами: q, i, j, u, p, e, j.

1. Заряд q [Кл]: q=q₊ + q_-..

2. Электрический ток i [А] – это направленное упорядоченное движение электрических зарядов в веществе или в вакууме; или это количество электричества (зарядов), проходящего в единицу времени через поперечное сечение проводника:

i = dq /dt.

Ток - величина скалярная, однако у него есть направление. Положительное направление тока – это направление движения положительных зарядов. Направление тока обозначают на проводе стрелкой. Ток считается заданным, если заданы его величина и положительное направление.

3. При протекании тока совершается работа. Мерой работы может быть потенциал. Электрический потенциал в данной точке j [В] численно равен работе, которую должны совершить силы электрического поля для переноса единичного положительного заряда из данной точки пространства в другую, потенциал которой принят равным нолю. За точку с нулевым потенциалом можно принять любую точку схемы, но только одну в пределах задачи.

4. В электрических цепях ток возникает под действием приложенного напряжения. Напряжение u [В] – это разность потенциалов двух точек схемы. Разность потенциалов между двумя точками (например, j₁ - j₂) определяют по работе, которую способны совершить силы электрического поля при переносе заряда из одной точки (например, точки 1) в другую (например, точку 2).

Напряжение u - величина скалярная, однако у него есть направление. Направление напряжения указывают либо стрелкой между точками, либо двойным индексом. u₁₂ = j₁ - j₂, а u₂₁ = j₂ - j₁ = - u₁₂. За положительное направление напряжения принимают направление от большего потенциала к меньшему. Это направление совпадает с направлением движения положительных зарядов. Поэтому считают, что и ток течет из точки с большим потенциалом в точку с меньшим потенциалом, т.о. на пассивных элементах (в приемниках) направление напряжения и тока совпадает.

Разность потенциалов в цепях создают активные элементы или источники ЭДС и источники тока, источники питания или генераторы. Внутри источников заряды перемещают сторонние силы. В активных элементах (источниках питания) происходит преобразование в электрическую энергию неэлектрической (химической, механической, тепловой), а в пассивных элементах (приемниках) – наоборот.

Если направление тока и напряжения неизвестно, то их задают произвольно. При этом в ходе расчетов могут получиться отрицательные значения. Это значит, что реальные направления противоположны выбранным, но полученный отрицательный результат не ведет к изменению направления.

5. При переносе зарядов электрическое поле совершает работу или, что тоже, поступает в приемник энергия. Скорость изменения энергии называют мощностью: p = dW/dt. Мощность характеризует интенсивность энергетического процесса и измеряют количеством генерируемой, отдаваемой, передаваемой энергией в единицу времени. Используя связь тока и заряда, получаю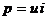т [Вт].

В отдельных участках цепи прохождение тока сопровождается преобразованием электрической энергии в неэлектрические формы, т.е. в этих участках энергия потребляется. В других участках наоборот происходит преобразование неэлектрических форм в электрическую энергию т.е. в этих участках энергия генерируется. По физическим соображениям из определения потенциала следует:

если ток на участке направлен так же, как и напряжение (т.е. заряды движутся под действием электрического поля), то в этом участке энергия потребляется (см. рис. 1.1.1);

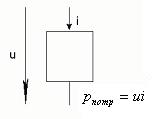
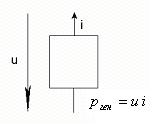
Рис.1.1.1 Рис.1.1.2

если ток на участке направлен противоположно напряжению (т.е. заряды движутся под действием сторонних сил), то в этом участке энергия генерируется (см. рис. 1.1.2).

Тогда , .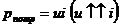

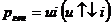Если токи, напряжения и т. д. во времени не изменяются, то их называют постоянными и обозначают заглавными буквами:

q ®Q, i®I, u®U, p®P, j®Φ.

Типовые элементы

1. Провод

На схемах провода не имеют сопротивления R_пр=0. Поэтому при любой их длине и любом токе все точки провода имеют один и тот же потенциал ( 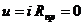). Длину провода и его конфигурация определяют из удобства изображения схемы.

2. Сопротивление R [Ом]

Главное свойство R - потребляет мощность.

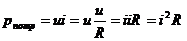[Вт].

Обратную величину называют проводимостью: 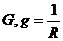[См].

3. Индуктивность L [Гн]

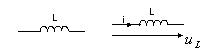
Главное свойство L - запасать энергию в магнитном пол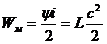е , где 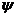- потокосцепление - сумма магнитных потоков, пронизывающих витки катушки. Индуктивность L – коэффициент пропорциональности 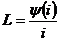[Гн],между потокосцеплением 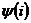магнитного потока, созданного током, проходящим через рассматриваемую катушку, с витками этой же катушки. По закону Ленца при L=const 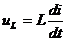. Таким образом, 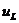зависит не от величины тока, а от скорости его изменения. При постоянном токе 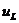=0 и индуктивность заменяется проводом.

4. Емкость С [Ф]

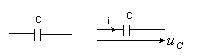
Главное свойство С - запасать энергию в электрическом поле.

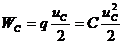, емкость 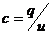- коэффициент пропорциональности между зарядами и напряжением между обкладками конденсатора. Тогда .

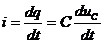Ток через емкость зависит не от напряжения, а от скорости изменения приложенного напряжения.

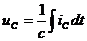. При 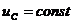ток через емкость не течет, и емкость заменяется разрывом.

Все рассмотренные выше элементы называют пассивными. Они не могут генерировать электрическую энергию. Есть и активные элементы, которые при определенных условиях могут генерировать электрическую энергию. Таких элементов два: идеальный источник напряжения (ЭДС) и идеальный источник тока.

1. Источник напряжения (ЭДС) e, E - это такой элемент, напряжение между зажимами которого при любом токе, по величине равно ЭДС.

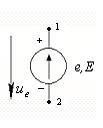
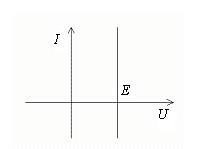
Стрелка внутри источника показывает направление возрастания потенциала внутри источника. Если е=0, то 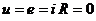на этом участке при любом токе. Это значит, что е=0 заменяется проводом R_пр = 0 и поэтому считают, что внутреннее сопротивление источника напряжения R_{вн е} = 0.

2. Источник тока j, J– это такой элемент, через который при любом напряжении между его зажимами проходит один и тот же ток равный величине источника тока. Если величина источника тока равна 0 (j=0), то i = j = u/R = 0, то при любом напряжении ток на этом участке будет равен нулю (разрыв цепи). Поэтому считают, что внутреннее сопротивление источника тока бесконечно: R_{вн j} = .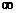

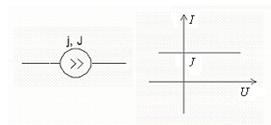
Источники тока обеспечивают смещения транзисторов; незаменимы в качестве активной нагрузки для усилительных каскадов с большим коэффициентом усиления и в качестве источников питания эмиттеров для дифференциальных усилителей; необходимы для работы таких устройств как генераторы пилообразного напряжения, интеграторы. Они необходимы для построения схем замещения транзисторов, ламп, любых активных устройств.

Рассмотренные источники ЭДС и тока называются автономными (неуправляемыми, независимыми). Существуют управляемые (зависимые) источники ЭДС и тока.

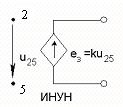
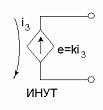
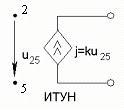
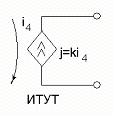
Рис.1.2.1

На рис.1.2.1 использованы следующие сокращения:

ИНУН – источник напряжения управляемый напряжением;

ИНУТ – источник напряжения управляемый током;

ИТУН – источник тока управляемый напряжением;

ИТУТ – источник тока управляемый током.

Используя стандартные элементы, можно строить схемы замещения реальных элементов цепи.

1.3 Топологические элементы схем

Кроме рассмотренных элементов существуют топологические элементы, которые позволяют описать структуру цепи.

Основные понятия:

1) Ветвь – соответствует участку цепи, в котором все элементы стоят последовательно, т.е. по которому протекает один и тот же ток.

2) Узел – место соединения трех и более ветвей (иногда даже двух ветвей – фиктивный узел).

3) Граф – условное изображение схемы, дающее положение всех узлов и ветвей без указания элементов. Графы делят на связные и несвязные.

связный граф несвязный граф

Связный – из любого узла можно попасть в любой другой по ветвям.

4) Любая часть графа называется подграфом.

5) Контур – замкнутый путь по ветвям.

6) Дерево – связный подграф, содержащий все узлы, но не образующий ни одного контура. Примеры деревьев:

7) Ветви, не вошедшие в дерево, называются ветвями связи.

8) Главный контур – это контур, полученный из ветвей дерева и только одной ветви связи.

Пример:

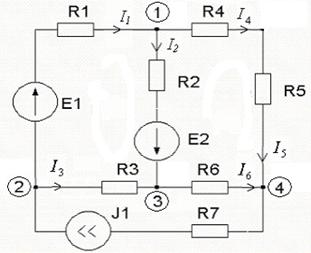
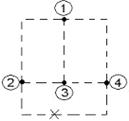
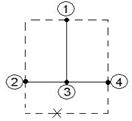
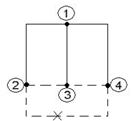
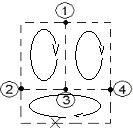
1.4 Основные законы цепей

1. Первый закон Кирхгофа

Алгебраическая сумма мгновенных значений токов ветвей, сходящихся в одном узле, равна нулю: .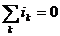

Токи, входящие в узел, берутся с одним знаком, а выходящие – с противоположным.

2. Второй закон Кирхгофа

Алгебраическая сумма мгновенных значений напряжений на всех элементах контура равна нулю: .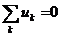

Выбирают направление обхода контура и тогда напряжения, совпадающие с направлением обхода контура, берут со знаком плюс, а направленные навстречу – со знаком минус. Так как напряжение на источнике ЭДС в точности равно самой ЭДС, а направлено в обратную сторону, удобно применять другую формулировку второго закона Кирхгофа: Алгебраическая сумма мгновенных значений напряжений на всех элементах контура, кроме источников ЭДС, равна алгебраической сумме мгновенных значений ЭДС этого же контура.

.

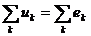Для напряжений правило знаков тоже, что и в первой формулировке, а ЭДС берут со знаком плюс, если направлено так же, как и обход контура.

3. В любой отдельно взятой цепи выполняется баланс мощностей

Сумма мощностей генерируемых равна сумме мощностей потребляемых:

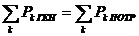или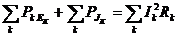

Пример:

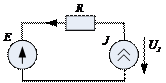
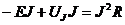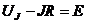, где и .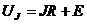

Метод уравнений Кирхгофа

Метод уравнений Кирхгофа позволяет рассчитать режим любой цепи, при любой форме сигнала, в любой момент времени.

Пусть требуется найти токи ветвей схемы, у которой число ветвей равно n_в и есть n_j источников тока, следовательно, (n_в - n_j) неизвестных токов. Значит столько необходимо составить уравнений по законам Кирхгофа, причем уравнения должны быть линейно независимыми.

По первому закону Кирхгофа получают (n_у –1) линейно независимых уравнений, где n_у - число узлов. По второму закону Кирхгофа остается написать (n_в - n_j) – (n_у –1) линейно независимых уравнений. Уравнения по второму закону Кирхгофа получаются линейно независимыми, если каждый контур отличается от всех других хотя бы одной ветвью, а все ветви, кроме ветвей с источниками тока, входят в выбранные контуры. В простых схемах количество контуров определяют так: “закрывают” ветви с источниками тока и определяют сколько получается ячеек, столько уравнений по второму закону Кирхгофа пишут.

Примерный порядок расчета

1. Выбирают положительное направление токов ветвей и нумеруют все узлы схемы.

2. Для (n_у –1) узлов записывают уравнения по первому закону Кирхгофа.

3. Для (n_в - n_j) – (n_у –1) контуров, не содержащих ветвей с источниками тока, записывают уравнения по второму закону Кирхгофа.

Или строят граф, выбирают дерево, определяют главные контуры. Для главных контуров, не содержащих источники тока, записывают уравнения по второму закону Кирхгофа.

4. Решают полученную систему уравнений относительно неизвестных токов ветвей.

5. Проверку правильности расчета режима цепи проводят по балансу мощностей.

Примечание:

1. Если в схеме есть управляемые (зависимые) источники, то систему уравнений по законам Кирхгофа дополняют столькими уравнениями связи, сколько управляемых источников в схеме. Каждое уравнение связи должно выражать величину управляемого источника через токи ветвей.

2. Если надо найти напряжение на всех элементах, то это делают в последнюю очередь. Напряжение на R определяют по закону Ома. Напряжение на источниках ЭДС известно: U_e=E. Для определения напряжения на источниках тока выбирают направление напряжения U_j и записывают уравнение по второму закону Кирхгофа для контура с источником тока: 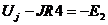, тогда .

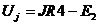Примеры составления уравнений по законам Кирхгофа.

1) Дано: 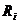, , 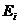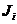. Найти .

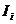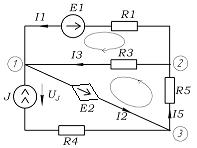Рис. 2.1.1

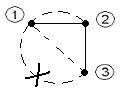
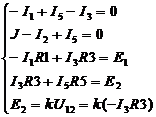
где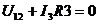

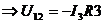
2)

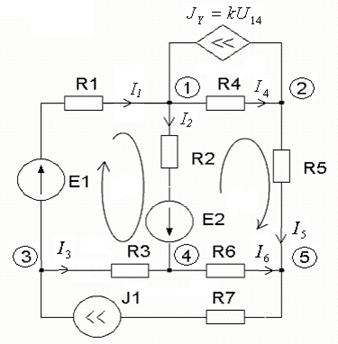
Рис. 2.1.2

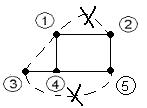
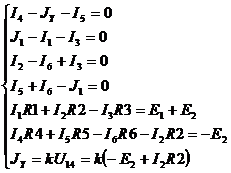
где =>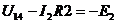

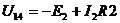
3)

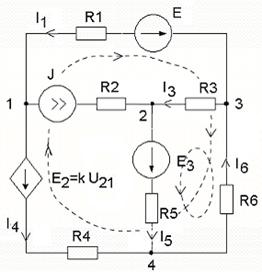
Рис. 2.1.3

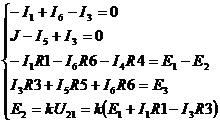
где .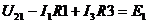

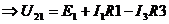Недостаток методауравнений по законам Кирхгофа состоит в том, что совместно приходится решать самую большую систему уравнений. Разработан ряд методов, позволяющих уменьшить число совместно решаемых уравнений: метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора, метод свертки, метод наложения.

Метод узловых потенциалов

Этот метод позволяет сократить число совместно решаемых уравнений по сравнению с методом уравнений Кирхгофа.

Идея метода состоит в следующем: если выразить ток каждой ветви по закону Ома для ветви, содержащей ЭДС и подставить полученное выражение в (n_У - 1) число уравнений первого закона Кирхгофа, получится система уравнений в относительно узловых потенциалов. Правда число потенциалов будет на единицу больше числа уравнений. Эту проблему решают так: т.к. ток в ветви зависит от разности потенциалов ее концов, не изменяя режима цепи, можно все потенциалы узлов схемы изменить на одну и ту же величину, причем на столько, чтобы один из потенциалов стал равен нулю (заземлить какой-то узел). После этого получаются уравнения стандартного вида.

Для некоторого узла k получится уравнение

,

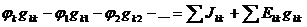где 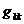- собственная узловая проводимость k-ого узла, она равна сумме проводимостей всех ветвей, подключенных к этому узлу;

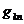- межузловая проводимость k-ого и n-ого узлов, она равна сумме проводимостей ветвей непосредственно соединяющих n-ый узел с узлом k для которого пишется уравнение;

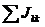- алгебраическая сумма величин источников тока, стоящих в ветвях, присоединенных к k-ому узлу;

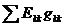- алгебраическая сумма произведений ЭДС, стоящих в ветвях присоединенных к k-ому узлу на проводимости этих ветвей.

У любого источника берется знак «+», если он направлен к узлу, для которого пишется уравнение.

Проводимость ветви есть величина обратная сопротивлению этой ветви.

Пример:

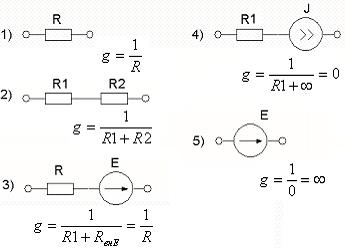
Ветвь 5) называется ветвью типа Е и проводимость вычисляется по особому правилу. Рекомендуемый порядок действий:

1. Выбирают узел, потенциал которого принимают равным нулю. Возможны 3 случая.

а. В схеме нет ветвей типа Е, тогда заземляют любой узел схемы. Записывают (n_У - 1) уравнений МУП, где n_У - число узлов схемы.

б. В схеме есть одна или несколько ветвей типа Е, но если их несколько, то все они между собой непосредственно соединены. Тогда обязательно заземляют один из узлов этих ветвей. Остальные узлы будут иметь известные потенциалы. Записывают ((n_У -1)- n_Е) уравнений

МУП, где n_Е – число ветвей типа Е.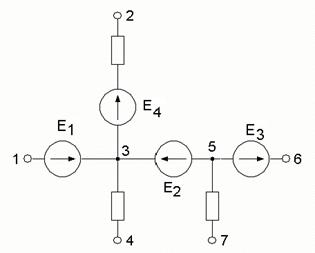

,

,

,

,

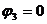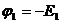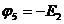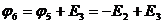в. В схеме есть несколько ветвей типа Е, но не все они между собой соединены – решать задачу МУП нельзя.

2. Для узлов, потенциалы которых остались неизвестными, записывают уравнения МУП стандартного вида и решают полученную систему.

Система уравнений должна быть полной – содержать столько уравнений, сколько неизвестных.

3. Токи ветвей записывают по закону Ома для участка цепи, содержащего ЭДС. В ветвях типа Е токи по закону Ома определить нельзя.

.

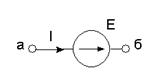
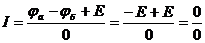Примечание: в ветвях типа Е токи находят по первому закону Кирхгофа в последнюю очередь.

Если в схеме есть управляемые источники, то к системе уравнений по МУП приписывают уравнения связи, в которых величины управляемых источников выражаются через узловые потенциалы.

Пример: Дано: 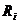, , 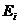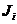. Найти: .

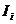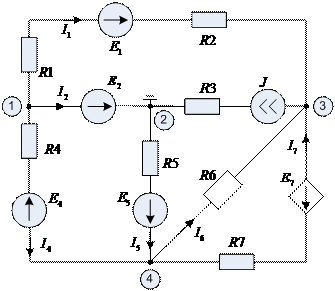
Пусть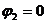

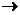
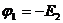
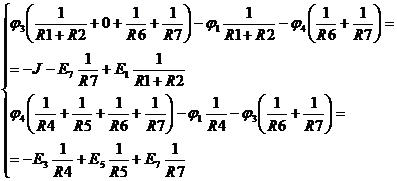
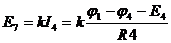
Решают эту систему и находят потенциалы 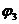и 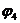. После этого находят токи ветвей:

, , , , ,

=> .

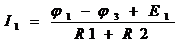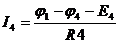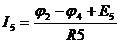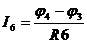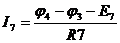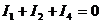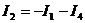Метод наложения

В любой линейной системе реакция на сумму воздействий равна сумме реакций на каждое воздействие в отдельности.

В цепях воздействие – это источники напряжения и источники тока, а реакция – это токи ветвей и напряжения между какими - то точками схемы. Поэтому любой ток или напряжение в линейной цепи с несколькими источниками равен сумме частичных значений тока или напряжения, вызванных действием каждого источника в отдельности. Свойство наложения (суперпозиции) справедливо только для токов и напряжений. Для мощностей этот принцип не выполняется, так как мощности элементов рассчитываются по нелинейным уравнениям.

Метод наложения основан на принципе наложения.

Примерный порядок расчета

1. Выбирают положительное направление токов ветвей и нумеруют все узлы схемы.

2. Исходную схему представляют в виде нескольких подсхем. В каждой подсхеме оставляют один или несколько автономных источников в общем случае одной и той же частоты, что определяется простотой расчета. Остальные автономные источники заменяют их внутренним сопротивлением. Все автономные источники должны войти в подсхемы, но только один раз.

3. Рассчитывают частичный режим в каждой подсхеме любым рациональным методом.

4. Режим в исходной схеме определяют как алгебраическую сумму частичных режимов. Если необходимо, то рассчитывают мощности.

5. Проверку правильности расчета режима цепи проводят по балансу мощностей или законам Кирхгофа.

Примечание: если в схеме есть управляемые (зависимые) источники, то их сохраняют во всех подсхемах.

Примерный порядок расчета

1. Выбирают положительное направление тока I_Н в ветви с нагрузкой.

2.Удаляют сопротивление нагрузки 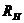и в месте разрыва изображают стрелку, направленную так же, как ток 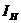в ветви нагрузки. Стрелка указывает направление напряжения холостого хода .

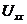3. Находят величину :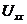

- записывают уравнение по второму закону Кирхгофа для фиктивного контура, включающего 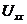и не вносящего дополнительных неизвестных U_J;

- в режиме холостого хода рациональным методом находят токи ветвей, входящие в уравнение для ;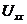

- рассчитывают величину .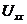

4. Определяют входное сопротивление R_BX относительно точек разрыва. Возможно несколько способов:

а) ,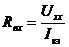

где 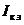- ток короткого замыкания, направленный также как ;

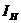б) при отсутствии в схеме управляемых источников расчет входного сопротивления рациональнее всего выполнять сворачиванием схемы к входным зажимам пассивной схемы, полученной из активной схемы, путем замены автономных источников энергии их внутренними сопротивлениями;

в) в схеме с автономными и управляемым источниками энергии автономные источники энергии заменяют их внутренними сопротивлениями. К зажимам полученной схемы подключают пробный источник и рассчитывают неизвестный пробный ток. Получают 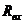как

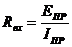
при одинаковом направлении .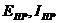

5. Рассчитывают ток через сопротивление нагрузки

.

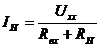Пример: Дано: , , , , , , .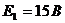

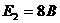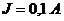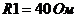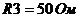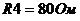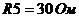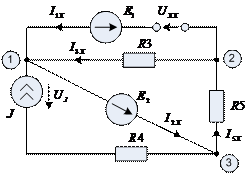
Рис. 2.6.1

=>

,

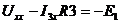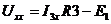
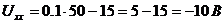где 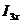- ток 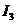в режиме холостого хода. 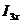можно найти:

1) из системы уравнений по законам Кирхгофа

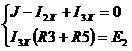
Откуда .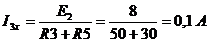

2) по методу наложения

, ,

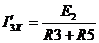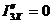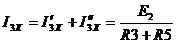
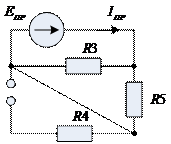
рис. 2.6.2

Согласно рис. 2.6.2:

.

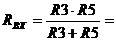
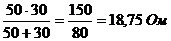Тогда: .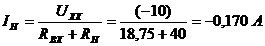

Алгебра комплексных чисел

Комплексным числом называют пару чисел, изображающих вектор на комплексной плоскости. Будем изображать комплексное число заглавной буквой с чертой внизу ( 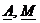). Вводится мнимая единица: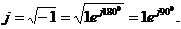

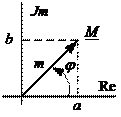
Комплексное число может быть представлено в разных формах:

– показательная форма: 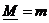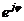- это вектор на комплексной плоскости, где 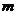- длина (модуль) вектора, 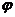- аргумент или фаза. Фазу всегда отсчитывают против часовой стрелки от положительного направления вещественной оси;

– алгебраическая форма: 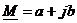– это точка на комплексной плоскости, где 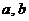- координаты по вещественной и мнимой осям, причем:

, ,

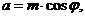
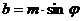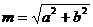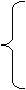
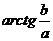, если ,

=

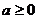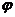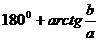, если < .

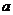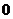Переход от одной формы записи комплексного числа к другой:

.

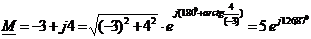Складывать комплексные числа предпочтительно в алгебраической форме либо геометрически по правилу параллелограмма: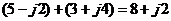

Вычитать комплексные числа удобно в алгебраической форме либо геометрически по правилу параллелограмма (вектор разности направлен из конца вычитаемого в конец уменьшаемого):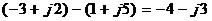

Умножать и делить комплексные числа удобнее в показательной форме:

; .

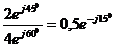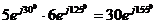Комплексные числа, не зависящие от времени, обозначают заглавными буквами с чертой внизу: 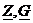, а комплексно сопряженные им числа обозначают еще и звездочкой сверху 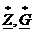: это числа, у которых та же вещественная часть, а мнимая с обратным знаком.

Комплексные числа, которые являются функциями времени, обозначают заглавными буквами с точкой сверху: 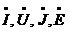, а комплексно сопряженные им числа обозначают заглавными буквами со звездочкой сверху : это числа, у которых тот же модуль, но фаза с обратным знаком.

Так как 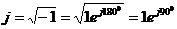, то умножить комплексное число на j это значит, не изменяя его модуля, увеличить фазу на 90⁰ или повернуть соответствующий вектор на 90⁰ против часовой стрелки. Разделить на j - наоборот:

.

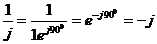Символический метод

Пусть есть комплексное число с линейно изменяющимся во времени аргументом: 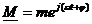. На комплексной плоскости это число представляет неизменный по длине век