Гамма-процентное значение случайной величины

Гамма-процентное значение tg случайной величины Т соответствует вероятности того, что случайная величина Т примет значение, большее tg:

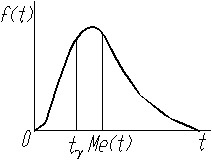
Гамма-процентное значение случайной величины можно определить по интегральной функции (рис.16), ее дополнению (рис.17) и дифференциальной функции (рис.18).

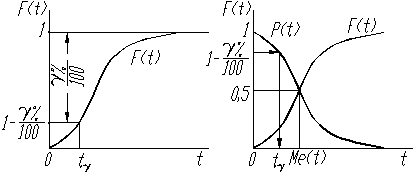Рис. 16. Интегральная функция Рис. 17. Дополнение интеграль-

ной функции

Гамма-процентное значение случайной величины является квантилем вероятности

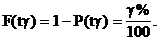
В теории надежности используются гамма-процентные значения ресурса, срока службы и срока сохраняемости.

Рис. 18. Дифференциальная Гамма-процентным назы-

функция вается ресурс (срок службы,

срок сохраняемости), который

имеет (и превышает) g процентов объектов данного типа.

Гамма-процентный ресурс характеризует долговечность при выбранном уровне 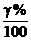вероятности неразрушения. Он назначается с учетом ответственности объектов, например:

1) для подшипников качения - 90%-ный ресурс;

2) для наиболее ответственных подшипников - 95%-ный ресурс;

3) если отказ опасен для жизни людей - 100%.

Медиана случайной величины

Медиана случайной величины является ее гамма-процентным значением при g=50%. Для медианы Me(t) одинаково вероятно, окажется ли случайная величина Т больше или меньше ее, то есть

P[T>Me(T)]=P[T<Me(T)].

Геометрически медиана является абсциссой точки пересечения интегральной функции распределения и ее дополнения (см. рис. 17). Медиану можно истолковать как абсциссу точки, в которой ордината дифференциальной функции делит пополам площадь, ограниченную кривой распределения (см. рис. 18).

В теории надежности медиану используют как числовую характеристику ресурса, срока службы, срока сохраняемости.

БЕЗОТКАЗНОСТЬ СИСТЕМЫ

Для анализа и расчета показателей надежности объектов, которые являются системами, состоящими из нескольких элементов, применяется метод структурных схем.

Метод позволяет определить безотказность объекта по известной безотказности каждого его элемента. Он заключается в том, что объект представлен в виде структурной схемы, на которой события или соответствующие им состояния элементов изображаются в виде последовательно или параллельно соединенных звеньев, выражающих безотказность отдельных элементов системы.

Рассмотрим безотказность объекта при последовательном, параллельном и смешанном соединениях элементов.

Безотказность объектов при последовательном

Соединении элементов

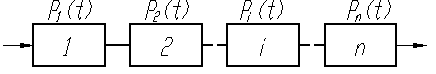Безотказность системы, изображенной на рис. 19, определяется при условии, что отказ каждого элемента является случайным не зависимым событием. Отказ любого элемента приводит к отказу всей системы.

Рис. 19. Последовательное соединение элементов

Вероятность P_c(t) безотказности системы в течение времени t при последовательном соединении элементов определяется по теореме умножения вероятностей независимых событий как произведение вероятностей безотказной работы ее элементов в течение того же времени:

P_c(t)= P₁(t) P₂(t)... P_i(t)... P_n(t)= (28)

где n - число последовательно соединенных элементов; P_i(t) - вероятность безотказной работы i-го элемента.

Вероятность безотказной работы системы можно выразить через интенсивность отказов ее элементов по формуле

P_c(t)=exp[-] exp[-]... exp[-]...

...exp[-]=exp[-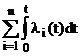]. (29)

Для равнонадежных элементов вероятности безотказной работы системы при Pi(t)=P(t) и l_i(t)=l(t)

P_c(t)= 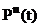= exp[ 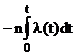]. (30)

Из формул (28)-(30) следует:

1. Вероятность безотказности системы уменьшается с увеличением числа последовательно соединенных элементов. Следовательно, при разработке объекта необходимо стремиться к возможно меньшему числу последовательно соединенных элементов.

2. Вероятность безотказности работы системы всегда меньше вероятности безотказности работы наименее надежного элемента. Следовательно, при разработке объекта необходимо выявлять наименее надежный элемент и повышать вероятность его безотказной работы.

Из формулы (29) следует, что интенсивность отказов системы в момент времени t равна сумме интенсивностей отказов составляющих ее элементов при любых распределениях вероятностей наработки на отказ элементов системы:

l_c(t)= l₁(t)+ l₂(t)+...+ l_i(t)+...+ l_n(t)=

Безотказность объектов при последовательном соединении элементов в период нормальной эксплуатации при внезапных отказах, когда явления старения и изнашивания объекта настолько слабо выражены, что ими можно пренебречь, является результатом воздействия многих случайных факторов при неизменных внешних условиях. Поэтому внезапные отказы в период нормальной эксплуатации имеют постоянную интенсивность l(t)=l=const.

Вероятность безотказной работы при постоянной интенсивности отказов имеет экспоненциальное распределение P(t) = =exp(-lt) и формулы (18), (19) принимают вид

P_c(t) 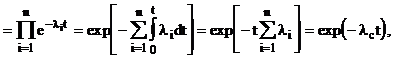(31)

где l_i - интенсивность отказов i-го элемента системы.

Из формулы (31) следует, что при экспоненциальном распределении длительности безотказной работы системы из последовательно соединенных элементов также будет экспоненциальным распределение с интенсивностью отказов l_c, равной сумме интенсивностей l_i отказов элементов:

l_c= = l₁+ l₂+...+ l_i+...+l_n. (32)

В этом случае среднее время безотказной работы системы

(33)

где T_ср.i. - среднее время безотказной работы i-го элемента.

Для однотипных элементов при l =l_i и T_ср.i. = T_ср. из формул (32) и (33) следует

l_c=nl, T_ср.i.= .

То есть интенсивность отказов системы в n раз больше интенсивности отказов одного элемента, а среднее время безотказной работы системы в n раз меньше среднего времени безотказной работы одного элемента.