Суть метода перемещений. Основная система МП

Суть метода перемещений (МП) рассмотрим на примере расчета рамы. Под действием приложенной нагрузки рама деформируется, а ее узлы получают линейные D_i и угловые q_i перемещения (рис. 6.1).

Идея МП заключается в том, чтобы выбрать эти перемещения D_i и q_i в качестве неизвестных.

Для упрощения расчета будем, как обычно, пренебрегать влиянием продольных сил на деформации. Тогда в нашем примере все линейные перемещения узлов будут равны: D_i = D .

В общем случае для определения числа неизвестных линейных перемещений - n_л нужно во все жесткие узлы рамы, включая опорные, ввести шарниры, а затем подсчитать число степеней свободы полученной шарнирно-стержневой системы по формуле (1.3):

n_л = 2У - С - С_О.

При этом число n_л будет равняться числу дополнительных линейных связей, необходимых для превращения полученной системы в геометрически неизменяемую.

Число неизвестных угловых перемещений q_i равняется, очевидно, числу незакрепленных жестких узлов рамы - n_у.

Общее число неизвестных метода перемещений n = п_у + n_л. Таким образом, в рассматриваемом примере n = 3 + 1 = 4.

В дальнейшем все линейные D_i и угловые q_i перемещения будем обозначать одинаково - Z_i.

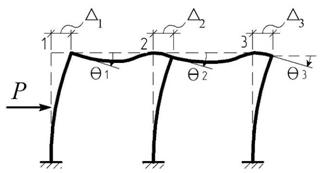
Рис. 6.1

Основная система МП образуется из заданной системы путем введения дополнительных связей, препятствующих угловым и линейным смещениям ее узлов.

Например, для рамы на рис. 6.2, а основная система получается наложением двух дополнительных связей (рис. 6.2, б). При этом первая связь является моментной и не препятствует линейному смещению соответствующего узла рамы. Для обозначения таких связей на схемах применяют также обозначения, показанные на рис. 6.2, в.

Введение связей превращает раму в совокупность однотипных элементов с одним или двумя жестко защемленными концами, для которых известны готовые решения (рис. 6.2, г).

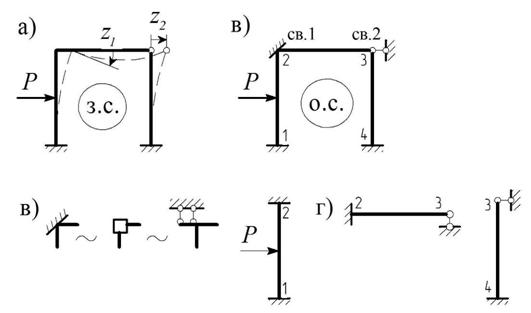
Рис. 6.2

Канонические уравнения метода перемещений

Если основную систему метода перемещений (ОС МП) загрузить нагрузкой, во введенных связях появятся реакции, которые отсутствовали в заданной системе (поскольку не было самих связей).

Обозначим через R₁ и R₂реакции во введенных связях и отметим, что поскольку ОС МП является статически неопределимой, эти реакции могут появляться не только под действием приложенной нагрузки, но и в ответ на кинематические воздействия.

Сообщим введенным связям перемещения Z₁ и Z₂, равные смещениям заданной системы и потребуем, чтобы ОС вела себя как заданная. Это означает, что реакции во введенных связях от смещения этих связей и от заданной нагрузки в сумме должны равняться нулю:

R₁ (Z₁, Z₂, P) = 0;

R₂ (Z₁, Z₂, P) = 0.

Воспользовавшись принципом суперпозиции, представим эти уравнения в виде:

r₁₁ Z₁+ r₁₂ Z₂ + R_1p⁰ = 0;

r₂₁ Z₁+ r₂₂ Z₂ + R_2p⁰ = 0,

где r_ij - реакция во введенной i-ой связи от единичного смещения j-ой связи, а R_ip⁰ - реакция в этой связи от заданной нагрузки.

Последние уравнения и называются каноническими уравнениями метода перемещений. В отличие от соответствующих уравнений метода сил эти уравнения имеют не геометрический, а статический смысл.

В общем случае для n неизвестных система канонических уравнений метода перемещений имеет вид:

Sr_ij Z_j + R_ip⁰ = 0; (i = 1, 2,…, n). (6.1)

Решив эту систему и определив неизвестные Z_j, можно найти внутренние усилия по формуле, аналогичной формуле (4.7):

M_p = M_p⁰ + S`M_i⁰Z_i. (6.2)

Примечание.

В соответствии с принципом суперпозиции перемещение любой фиксированной точки i заданной системы можно найти как сумму двух: перемещения этой точки в ОС МП вследствие смещения введенных связей, и ее перемещения в той же системе под действием заданной нагрузки (рис. 6.3):

Δ_ip = Δ⁰_ic + Δ⁰_ip . (6.3)

Последнее соотношение является аналогом формулы (6.2) для перемещений.

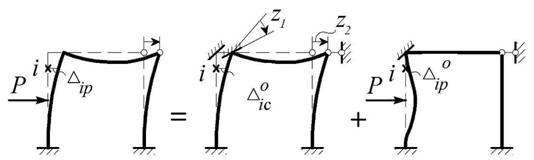
Рис.6.3