Графическое изображение рядов распределения.

Графическое изображение рядов распределен.облегчает их анализ и позволяет судить о форме распределения. Для графического изображения дискретного ряда применяют полигон распределен. Но рекомендуется брать соотношения масштабов 1:2. Напр. имеем распределен. рабочих по квалификации:

Квалиф. 1 2 3 4 5 6 7 8

Чел. 3 5 8 12 17 9 5 3

Для графич.изображен.вариацион. рядов примен.гистограммы.

Например, имеем следующее распределен.раб.по стажу

Стаж (лет)	Численность раб.
Абсолютн.	Накоплен.
0-5
5-10		4+12=16
10-15		16+7=23
итого

Гистограмма может быть преобразована в полигон распределения, путем соединения середин верхних сторон прямоу-гольников отрезками прямых. При построение гистограммы для вариационного ряда с неравными интервалами на ось ординат наносят плотность интервала. Тогда высоты прямоугольников гистограммы отражают плотность распределения. При увеличение числа наблюден., увеличивается и число групп, интервального ряда, что приводит к уменьшению величины интервала. В нашем примере надо взять за интервал распределение раб.по стажу не 5-летний период, а 2-летний интервал. При этом возрастет число сторон полигона распределения и ломанная линия превратится в крив.распределения. Она характ.закономерность частот внутри однокачественной совокупности.

Показатели центра распределения.

Для обобщения хар-ки значения признака в вариацион.ряду исп. ср. арифм., мода и медиана. Рассмотрим расчет показателя центра распределения, моды и медианы для вариац.рядов. Для дискретного ряда среднее рассчитывается по формуле ср. взвешенного: x =∑x f/∑f

В интервальном вариац.ряду ср. арифм.опр.по формуле:x =∑x` f/_∑f, где x`- середина интервала. В отличие от степенных средних, мода и медиана не явл.описателем среднего. Мода – это величина признака, который наиболее часто встреч. в данной совокупности. Напр.имеются разряды раб. и число чел., имеющих эти разряды.

Разряды: 1 2 3 4 5 6 7 8

Число чел.: 3 5 8 12 17 9 5 3

Мода =5 разряд.

Если две моды, то имеем бимодальное распределение. Если больше двух, то моды нет. Для определения моды в интервальном вариац. ряду с равными интервалами исп.: Mo= x_Mo+i(f_Mo-f_Mo-1)/ (f_Mo-f_Mo-1)+(f_Mo-f_Mo+1), x_Mo – начальное значение интервала, содержащего моду, i – величина равного интервала, f_Mo, f_Mo-1, f_Mo+1, - частоты модального, предшествующего моде и следующего за модой интервала. Медиана – это значение признака. стоящего в середине ранжированного ряда. Номер места медианы: N_Me= (n+1)/2, n – число единиц совокупности. Напр.: Разряд: 1 2 3 4 5 6 7 8

Чел.: 2 5 8 11 9 7 4 5 =51

N_Me= (51+1)/2=26, Ме= 4 разряд. Для интервального ряда с равными интервалами Ме определяется по следующей формуле: Ме= x_Mе+i(0,5∑f - S_{Me-1_})/ f_Mе, x_Mе - начальное значение интервала, содержащего медиану, i – величина равного интервала, число единиц, S_Me-1 - сумма накопленных частот интервала, предш-его медианному, f_Mе - частота медианного интервала. В случае, если мы имеем исх.данные с неравными интервалами, а нам нужно определить Мо и Ме, то произво-дится вторичная группировка и образуются гр. с равными интервалами. Мо и Ме можно опр.графически. Мо применяется при планировке массового вкуса одежды и обуви, при изучении товарооборота и др. Ме применяется при экспертных оценках и контроле качества продукции. Если сформулировать осн.правила для выбора ср.арифм., Мо и Ме в качестве центра распределения, то в симметричных рядах все они равны между собой, но лучше ср. арифм. Для ассиметричных рядов лучше Ме, т.к. она нах. между ср. арифм. и Мо.

Показатели вариации.

Средн.величина дает обобщаю-щую хар-ку савокупности, однако при значит.рассеивании индивид значения признака она не достаточна. Для измерения вариации применяются различные обобщающие показатели. Напр. имеются данные о з/пл раб.двух бригад.

I: 105 150 185; II: 70 120 250

Их средн.одинаковы x_I,II=∑x/n=146/ Но структура з/пл различается. Размах вариации - это разность между mах и min значением признака. R=x_max - x_min. R_I=185-105=80; R_II=250-70=180. R_I< R_II в 2,25 раза. Размах зависит только от крайних значений, поэтому применим только для достаточно однородной совокупности. Нужны показатели, учитывающие колебания всех значений признака. Ср.линейное отклонение представляет собой ср. арифметическое из абсолютных отклонений всех значений признака от средней. Для первичного ряда: d_ср= ∑│x - x_ср│/n, для вариац.ряда d_ср= ∑│x - x_ср│f/∑f, d_срI=146-105+[146-150]+[146-185]/3= =28, d_срII=66,6 ; d_{ср I} < d_срII в 2,4 раза.

Дисперсия σ² это среднее из квадратов отклонения вариантов значения признака от их средней величиныσ²=∑( x-x )² /n. Для вариацион.ряда: σ²=∑( x-x )²f/∑ f. σ²_I=(41²+(-4)²+(-39)² )/3=1072,6. σ²_II =5756, σ²_I < σ²_II ~ в 5 раз. Дисперсия имеет самостоятельное значение в ст-ке и относится к числу важнейших показателей вариации. Для альтернативных признаков σ²=p(1-q)=pq; σ=√pq, p – доля единиц, обладающих определенным признаком, а q- нет Т.к. p+q=1, то σ² <=0,25. Ср.квадратич.отклонение: 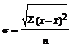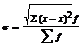-для вариац.ряда σ_I=√1072,6=32.7; σ_II =75.86, σ_I < σ_II ~ в 2 раза. Ср. квадратич. отклонение одно-временно с дисперсией явл.самым распространенным показателем. Для умеренно ассиметричных распределений d=0,8σ. Ср. линейн. и квадратич. отклонение величины именованные, но даже если они равны между собой, а ср. арифм. различны то для каждой сов-ти они имеют различн. знач-е. Поэтому рассчитывают относ. пок-ль колеблемости: υ_σ =(σ/x)100%, υ_d=(d/x)100%, υ_σI =(32,7/146)100%=22.4%, υ_dI=(28/146)100%=19,2%, υ_σII =51,9%; υ_dII=45.6%. Также коэф. вариации исп. для хар-ки однородности совокупн. Если он <33%, то считают что совокупн.однородна. Показатели вариац.явл. мерой надежности средних. Чем меньше d_ср σ² υ , тем однороднее изучаемая совокупность и надежнее получаемое среднее. По правилу 3-х σ, в нормальн.рядах отклонение от ср.арифм.не превосходит + - 3σ встречается в 997случаях из 1000, + - 2σ в 954 случаях, + - 1σ в 683 случаях. Зная их среднее из σ можно предста-вить весь вариацион.ряд. Напр. ср. з/пл 150 тыс.р., а σ=32.7, то при 3σ. min: 150-3’ 32.7=51.9. max: 150+3’ 32.7=248.1

Дисперсия и ее свойства.

Расчет дисперсии в ряде случаев явл. весьма трудоемким. Его можно упростить, если воспользо-ваться некоторыми его матем. св-вами. 1)Дисперсия постоянного числа=0. Если х=a, то σ= ∑(х-a)f/∑f =0. 2)Если все значения признака уменьшить или увеличить на постоянное число а, то дисперсия от этого не изменится. Т.е. дисперсию можно исчислитьпо отклонениям постоянного числа а. 3)Если все значения признака уменьшить или увеличить в к-раз, то дисперсия от этого изменится в k² раз. Т.е. можно все значения признака уменьшить в к раз и исчислить дисперсию, а затем ее умножить на k² . Дисперсия признака = разности между средним квадратом значения признака и квадратом x средней. 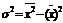. Рассмотрим пример счета дисперсии с учетом их св-тв. Это способ моментов или условного 0.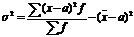

Правило сложения дисперсий.

На вариацию признака влияют различные факторы. Все они делятся на случайн. и систематич. Поэтому вариация может быть случайной и систематической. Необход.ее определить и выявить ее роль в общей вариации. Общая вариация совокупности является результатом действия всех причин и измеряется общей дисперсией: 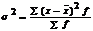. Вариация групповых средних измер.отклонением групповых ср. от общей ср. и отражает влияние фактора по которому произведена группировка. Обозначается 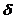. 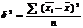, , 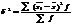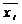- групповые средние. Остаточная или внутригрупповая вариация выражает отклонение отдельных значений признака в каждой группе от их групповой средней и отражает влияние всех прочих факторов, кроме положен-ного в основе группировки. Поскольку групповая дисперсия в каждой группе: 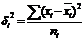,то остаточную вариацию будет отражать среднее из групповых дисперсий, рассчитанное по формуле: 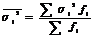. Очевидно, что общая вариация признаков совокупн. определяется как сумма вариаций групповой ср. и остаточной вариации. Это равенство находит свое отражение в сложение дисперсии 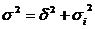. Логика этого з-на проста: общая дисперсия, возникающая под воздействием всех факторов должна быть равна сумме дисперсий, возникающих за счет факторов группировки и под воздействием всех прочих факторов. Это равенство, имеющее строго матем. док-во известно как правило сложения дисперсии. Оно позволяет находить общую дисперсию по групповым показателям. Отношение межгрупповой диспер-сии к общей назыв. коэф. детерминации. Корень квадратный из него назыв. корреляционным отношением и измер. зависимость между группировочным и результативным признаком 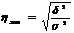. Значение 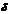эмпирич max при 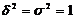, когда влияние прочих факторов равно 0. 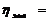min, при 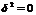, 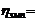0, когда влияние группировочного признака результата = 0.