Какие утверждения об усатых ящиках верны?

1. 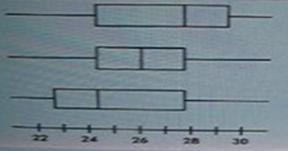они все симметричны

2. первое распределение скошено вправо

3. третье распределение скошено влево

4. второе распределение симметрично

Какие ранги будут соответствовать данным показателям

1. 1, 5, 5, 4, 17, 17, 17, 8, 9

2. 1, 2.5, 2.5, 4, 6, 6, 6, 8, 9

3. 2, 2, 3, 7, 5, 6, 7, 21, 23

Дисперсия

1. этохарактеристика рассеивания наблюдений около средней

2. является интервальным параметром распределения

3. равна квадрату среднеквадратического отклонения

4. на основе оценивания дисперсии построен дисперсионный анализ

1 3 4

Что из перечисленного обращается в ноль, если все значения в выборке одинаковы

1. дисперсия

2. среднее значение

3. стандартное отклонение

4. размах выборки

1 3 4

Главной задачей применения метода наименьших квадратов для построения линии регрессии является

1. Провести линию через все точки выборки

2. Минимизировать сумму всех наблюдений

3. Минимизировать сумму квадратов остатков

Выберите правильные границы для сильной корелляционной связи

1. От 0,7 до1

2. От 50до 100

3. От 0,3 до 0,7

4. От 0 до 0,3

5. От 1 до 3

Сопоставьте значение коэффициента корреляции r и силу и характер связи

1. +1 а. слабая прямая

2. -0,69 б. слабая обратная

3. -0,3 в. средняя обратная

4. +0,25 г. сильная прямая

5. +0,8 д. полная прямая

4а 3б 2в 5г 1д

Корреляционная связь является обратной и сильной, если значение коэффициента корреляции принадлежит интервалу

1. от0 до 0,3

2. от -0,7 до -0,3

3. от -0,7 до -1

4. от -0,3 до 0

5. от 0,7 до 1

Выберите верное утверждение о коэффициенте корреляции

1. коэффициент корреляции и коэффициент регрессии могут иметь разные знаки

2. коэффициент корреляции равный 1 означает полную причинно-следственную связь между переменными

3. коэффициент корреляции +0,87 и -0,87 отражают одинаковую силу связи

2 3

Коэффициент корреляции измеряется в пределах

1. от 0 до 5

2. от1 до 100

3. от -1 до +1

4. от -5 до +5

5. от минус бесконечности до плюс бесконечности

Что из перечисленного может влиять на коэффициент корреляции

1. изменение размерности переменных

2. перестановка переменных местами

3. добавление одной и той же константы ко всем значениям переменной Х

4. исключение крайних значений (выбросов)

Сформулируйте нулевую гипотезу для анализа таблиц сопряженных признаков

1. нет зависимости между оцениваемыми признаками

2. есть зависимость между оцениваемыми признаками

3. нет различия между оцениваемыми признаками

9. какой вывод следует сделать, если F_набл = 0,038,а F_критич = 4,196?

1. Нет оснований отвергать основную гипотезу, следовательно, фактор не влияет на результат

2. Нет оснований отвергать основную гипотезу, следовательно, фактор влияет на результат

3. Основная гипотеза должна быть отвергнута, следовательно, фактор влияет на результат

4. Основная гипотеза должна быть отвергнута, следовательно, фактор влияет на результат

За основную гипотезу в однофакторном дисперсионном анализе принимают предположение, что

1. Фактор не оказывает влияния на результат

2. Фактор не оказывает влияния на результат

3. Средние значения различаются статистически значимо

4. Средние значения различаются статистически значимо

При перекрестной модели двухфакторного дисперсионного анализа необходимо вычислить

_1. S²_I

_2. S²_II

_3. S²_{гл факт}

_4. S²_{подч факт}

_5. S²_подч

_6. S²_ост

1 2 6

Основные свойства функции выживаемости

1. При времени, близком к нулю, выживаемость равна единице

2. При времени, близком к бесконечности, выживаемость равна единице

3. При времени, близком к нулю, выживаемость равна нулю

Выживаемость

1. Это вероятность прожить время, большее t с момента наблюдения

2. Это способность половины исследуемых объектов прожить более половины времени выживаемости

3. Измеряется только в часах

4. Измеряется в процентах или долях

5. Может быть равна 2,01