ТЕМА №6.6 Нормальное распределение
1. Верно или неверно: в нормальном распределении среднее значение, медиана и мода имеют одинаковое значение и график распределения симметричен:
1) Верно
2) Неверно
Какие два параметра популяции определяют форму нормальной кривой (они делают нормальную кривую высокой и узкой или низкой и широкой).
1) Медиана и среднее значение
2) Мода и стандартное отклонение
3) Медиана и стандартное отклонение
4) Среднее значение и мода
5) Среднее значение и стандартное отклонение
По отношению к стандартному отклонению, где находятся точки изгиба нормальной кривой?
1) На одно стандартное отклонение влево И на одно стандартное отклонение влево от среднего значения
2) На одно стандартное отклонение влево И на два стандартных отклонения вправо от среднего значения
3) На два стандартных отклонения влево И на два стандартных отклонения вправо
4) В точках, соответствующих среднему значению и медиане
5) На половине расстояния между средним значением и двумя отдельно лежащими значениями
Предположим, что у нормальной кривой А и нормальной кривой Б одинаковые средние значения популяции. Предположим также, что у А стандартное отклонение больше, чем у Б. Которая кривая выше и почему?
1) Кривая А выше, поскольку имеет меньше точек изгиба
2) Кривая А выше, поскольку чем меньше стандартное отклонение, тем шире изгиб кривой
3) Кривая Б выше, поскольку её медиана больше
4) Кривая Б выше, поскольку чем меньше стандартное отклонение, тем уже изгиб кривой
5) У изгибов кривых одинаковая высота
5. ??? Вы измеряете вес индивидов популяции W и обнаруживаете, что вес имеет нормальное распределение со средним µ=70 кг и стандартным отклонением σ = 10 кг. На каком расстоянии от математического ожидания находится значение 90 кг?
1) -1σ
2) 1σ
3) 2σ
4) 0σ
5) -2σ
6. Вы измеряете вес индивидов популяции W и обнаруживаете, что вес имеет нормальное распределение со средним µ=70 кг и стандартным отклонением σ = 10кг. Для популяции W, каким процентилем является вес в 70 кг?
1) 50-й процентиль
2) 10-й процентиль
3) 30-й процентиль
4) 75-й процентиль
5) 90-й процентиль
7. Подходящей записью для обозначения нормального распределения со средним значением 250 и стандартным отклонением 25 является:
1) N(250;1)
2) X(250;25)
3) N(250;25)
4) N(25;250)
5) Никоторый из перечисленного
8. Имеется нормальная кривая со средним значением φ. Увеличиваем стандартное отклонение этой кривой. Как изменится сама кривая?
1) Новая нормальная кривая станет более плоской и узкой
2) Новая нормальная кривая станет более плоской и широкой
3) Область под кривой на отрезке в одно стандартное отклонение увеличивается
4) Среднее значение увеличивается на столько, на сколько увеличивается стандартное отклонение
5) Никоторое из перечисленного
Какие из утверждений верны?
1) Область ниже нормальной кривой всегда равна 1. Неважно, каковы среднее значение и стандартное отклонение
2) Чем меньше стандартное отклонение нормально кривой, тем выше и уже график
3) Нормальные кривые с разными средними значениями имеют центром разные числа
1 2 3
Какое из утверждений верно?
1) Область ниже стандартной нормальной кривой в интервале от 0 до 2 в два раза больше области в интервале от 0 до 1
2) Область ниже стандартной нормальной кривой в интервале от 0 до 2 в два раза меньше области в интервале от -2 до 2
3) Для стандартной нормальной кривой межквартильный ряд примерно равен 3
Популяции P1 и P2 с нормальным распределением имеют одинаковые средние значения. Однако, стандартное отклонение P1 в два раза больше такового у P2. Что можно сказать о проценте наблюдений, попадающих в границы стандартного отклонения среднего значения каждой популяции?
1) Процент для Р1 в два раза больше процента для Р2
2) Процент для Р1 больше, но не в два раза, чем процент для Р2
3) Процент для Р2 в два раза больше процента для Р1
4) Процент для Р2 больше. Но не в два раза, чем процент для Р1
5) Проценты одинаковы
12. ??? Представлены следующие две нормальные кривые: 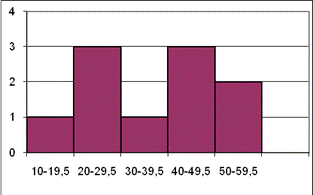
У которой больше среднее значение и больше стандартное отклонение?
1) Больше среднее значение, А; больше стандартное отклонение, А
2) Больше среднее значение, А; больше стандартное отклонение, Б
3) Больше среднее значение, Б; больше стандартное отклонение, А
4) Больше среднее значение, Б; больше стандартное отклонение, Б
5) Больше среднее значение, Б; равные стандартные отклонения
Какие из утверждений верны?
1) Во всех нормальных распределениях среднее значение и медиана равны
2) Все колоколообразные кривые имеют нормальное распределение для некоторых µ и σ
3) Фактически, вся область ниже нормальной кривой расположена в 3 стандартных отклонениях среднего значения вне зависимости от конкретных среднего значения и стандартного отклонения
1 3
Какие из утверждений верны?
1) Как и нормальное, t-распределения всегда асимметричны
2) Как и нормальное, t-распределения всегда холмообразны
3) T-распределения менее плоские, чем нормальные, что означает меньшую вероятность на концах и большую в центре, чем у нормального
1 2
