Методика нахождения выборочного уравнения прямой линии регрессии

Пусть требуется по данным корреляционной таблицы найти выборочное уравнение прямой линии регрессии Y на Х.

Вычислим сначала выборочный коэффициент корреляции. Можно значительно упростить расчет, если к условным вариантам (при этом величина 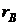не изменится)

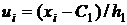и

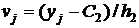
В этом случае выборочный коэффициент корреляции вычисляют по формуле

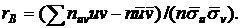
Величины 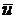, , 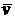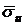и 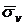можно найти методом произведения, а при малом числе данных – непосредственно исходя из определенных этих величин. Остается указать способ вычисления 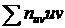, где 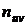– частота пары условных вариант ( , ).

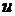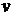Можно доказать, что справедливы формулы:

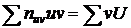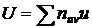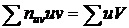, где ,

, где .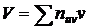

Для контроля целесообразно вычислить расчеты по обеим формулам и сравнить результаты; их совпадения свидетельствуют о правильности вычислений.

Напишем искомое уравнения в общем виде:

. (*)

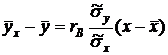Поскольку при нахождении 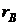уже вычислены 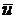, , 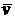, , 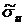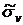то целесообразно пользоваться формулами:

, , , .

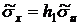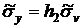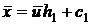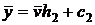Пример.Найти выборочное уравнение прямой линии регрессии Y на X по данным корреляционной таблицы

Y	X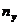
			–	–	–	–
	–			–	–	–
	–	–				–
	–	–
	–	–	–
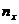							n=200

Решение. Перейдем к условным вариантам: 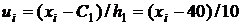(в качестве ложного нуля 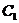взята варианта x=40, расположенная примерно в середине вариационного ряда; шаг 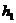равен разности между двумя соседними вариантами: 20–10=10) и 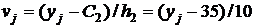(в качестве ложного нуля 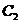взята варианта y=35, расположенная в середине вариационного ряда; шаг 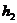равен разности между двумя соседними вариантами: 25–15=10).

Составим корреляционную таблицу в условных вариантах. Практически этоо делают так: в первом столбце вместо ложного нуля 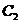(варианты 35) пишут 0; над нулем последовательно записывают –1, –2; под нулем пишут 1, 2. В первой строке вместо ложного нуля 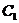(варианты 40) пишут 0; слева от нуля последовательно записывают –1, –2, –3; справа от нуля пишут 1, 2. все остальные данные переписываются из первоначальной корреляционной таблицы. В итоге получим корреляционную таблицу в условных вариантах.

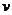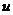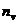–3	–2	–1
–2			–	–	–	–
–1	–			–	–	–
	–	–				–
	–	–
	–	–	–
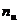							n=200

Теперь для вычисления искомой суммы 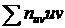составим расчетную таблицу. Пояснения к составлению таблицы.

1. В каждой клетке, в которой частота 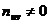записывают в правом верхнем углу произведение частоты 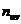на варианту 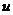. Например, в правых верхних углах клеток первой строки записаны произведения: 5*(–3)=–15; 7*(–2)=14.

2. Складывают все числа, помещенные в правых верхних углах клеток одной строки и их суму записывают в клетку этой же строки столбца 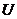. Например, для первой строки 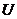=–15+(–14)=–29.

3. Умножают варианту 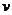на 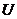и полученное произведение записывают в последнюю клетку той же строки, то естьв клетку столбца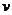 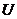. Например, в первой строке таблицы 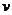=–2, 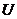=–29; следовательно,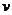 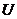=(–2)*(–29)=58.

4. Наконец, сложив все числа столбца 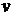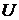, получаем сумму 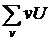, которая равна искомой сумме 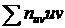. Например, для таблицы имеем 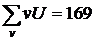; следовательно, искомая сумма .

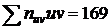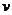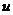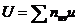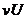–3	–2	–1
–2	–15 –10	–14 –14	–	–	–	–	–29
–1	–	–40 –20	–23 –23	–	–	–	–63
	–	–	–30			–	–28
	–	–	–10
	–	–	–
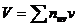	–10	–34	–13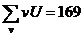

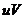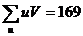Для контроля аналогичные вычисления производят по столбцам: произведения 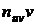записывают в левый нижний угол клетки, содержащей частоту 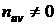; все числа, помещенные в левых нижних углах клеток одного столбца, складывают и их сумму записывают в строку V; далее умножают каждую варианту 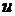на V и результат записывают в клетках последней строки.

Наконец, сложив все числа последней строки, получают сумму 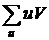, которая также равна искомой сумме 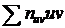. Например, для таблицы имеем 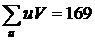; следовательно, .

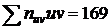Величины 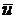, , 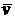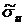и 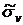можно вычислить методом произведений; однако, поскольку числа 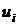, 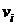малы, вычислим 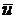и 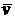, исходя из определения средней, а 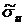и 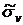– используя формулы:

, .

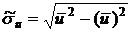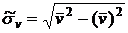Найдем 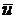и :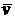

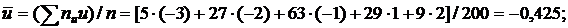
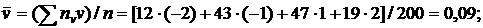
Вычислим вспомогательную величину 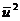, а затем :

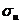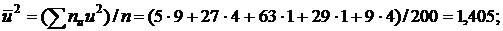
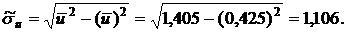
Аналогично получим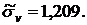

Найдем искомый выборочный коэффициент корреляции, учитывая, что ранее уже вычислена сумма :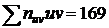

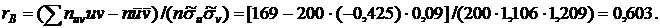
Итак,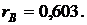

Остается найт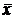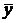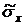и , , и :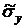

; .

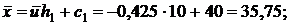
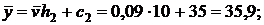
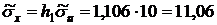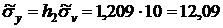Поставим найденные величины в уравнение (*), получим искомое уравнение

,

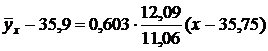или окончательно

.

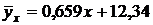Сравним условные средние, вычисленные: а) по этому уравнению; б) по данным корреляционной таблицы. Например, при х=30:

а) ;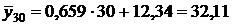

б) .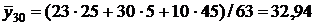

Как видим, согласование расчетного и наблюдаемого условных средних – удовлетворительное.