Линейный коэффициент корреляции и коэффициент Фехнера. Проверка линейного коэффициента корреляции на значимость.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:

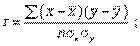
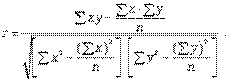
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.

коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле

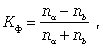
где n_a - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; n_b - соответственно количество несовпадений.

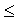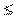Коэффициент Фехнера может изменяться в пределах -1,0 К_ф +1,0.

проверке гипотезы H0 остатистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфактопределяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

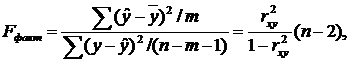
где n – число единиц совокупности;

m – число параметров при переменных x.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если Fтабл< Fфакт, то H0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл> Fфакт, то H0 – гипотеза не отклоняется и признается статистическая незначимость, надежность уравнения регрессии.

2. t-критерий Стьюдента используется для оценки статистической значимости коэффициентов регрессии и коэффициента корреляции.

В качестве основной гипотезы вы­двигают гипотезу H0 о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактиче­ским) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (ко­торые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).

Табличное значение оп­ределяется в зависимости от уровня значимости (a) и числа степеней свободы, которое в случае линейной парной рег­рессии равно (n-2) , n - число наблюдений.

Если фактическое значение t-критерия больше таб­личного (по модулю), то считают, что с вероятностью (1-a) параметр регрессии (ко­эффициент корреляции) значимо отличается от нуля.

Если фактическое значение t-критерия меньше таб­личного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр регрессии (коэффициент корреля­ции) незначимо отличается от нуля при уровне значимости a.

Фактические значения t-критерия определяются по формулам:

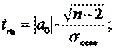
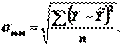где

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

где r - оценка коэффициента корреляции, полученная по наблюдаемым данным. tтабл остается прежним.

3. Адекватность регрессионной модели оценим с помощью средней ошибки аппроксимации – среднее отклонение расчетных значений от фактических:

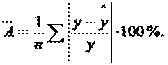
Допустимый предел значений 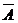– не более 8-10%.